ПРОМЫШЛЕННАЯ ТЕПЛОПЕРЕДАЧА ТЕОРИЯ И ЕЕ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ. ОСНОВНЫЕ ЧИСЛОВЫЕ ПРИМЕРЫ
ПОТЕРЯ ДАВЛЕНИЯ В ТРУБЕ И В ТРУБНОМ ПУЧКЕ
В следующем разделе будет рассмотрена тесная физическая и экономическая связь между теплопередачей и потерей давления. Чем выше коэффициент теплоотдачи конвекцией, тем меньше и дешевле теплообменник, ио тем дороже его эксплуатация за счет увеличенной мощности вентилятора. Поэтому, проектируя теплообменник, инженер должен знать не только значенйя коэффициентов теплоотдачи, но и потери давления.
Потери давления в трубе были исследованы точно и довольно исчерпывающе О. Фрицше [197]. В результате Фрицше пришел к следующему уравнению:
Dp 9,38- 10—4 0.852 1.852 , /orvi
------- — = —1--------------- • Y НО ММ ВОД. ст/л*. (801)
Dl d1»269
Для практического применения это уравнение лучше дать в несколько иной форме. По уравиению (161)
W • п = w0 • То, (802)
Где w м/сек— скорость, а у кг/м3 — удельный вес среды при данных условиях, т. е. при давлении Р атм и температуре Т°К в отличие от соответствующих значений w0 и у о, отнесенных к нормальным условиям (760 мм рт. ст. и 273° К).
Сообразно с этим уравнение (801) преобразуется следующим образом:
TOC o "1-5" h z --- — = - Р— . (а>0 • то)0,852 • wmm вод. ст/м. (803)
* dl d1-г69
Известно, что
Т* ,
W — xsdq-- — м/сек, (804)
0 273. я
1
Где Р — давление, атм (1 атм = 760 мм рт. ст. В отличие от 1 аг=760 кг/см2).
Если также учесть, что —^— практически то же самое, что
И перепад давления на 1 м длины трубы Ар, то уравнение (803) с учетом уравнения (804) примет вид
Др = 9,38-нг^. „J. M3 . #*** . _J_^вод. ст/л. (805)
Dl,269 273 Р
Так как для воздуха и дымового газа примерно справедливо ^6,852 = 1,24, то для них
11,7 • a>i'852 • — - f— L
О 970 р
Ар~--------------------------------- —лшвод. ст. (806)
И 104.d1.269
Кроме вышеназванных обозначений, здесь L — длина трубы и d— ее диаметр в метрах.
Если диаметр трубы выразить в миллиметрах, то в уравнениях (805) и (806) можно избежать сомножителя 104. Если диаметр jb свету обозначим через D мм, то уравнение (805) запишется
Лр = ! гбТ ' wo'852 ' То’852 ‘ ------- —мм вод. ст/л (807)
D • 273 Р
И уравнение (806) для воздуха и дымового газа
|
Д Р = _ , - • <852 ■ —- • Lmm вод. ст. (808) |
D1-269 273 Р
Потеря давления в трубных пучках впервые была исследована Г. Рейером (см. стр. 185) на моделях. Однако эти измерения сейчас нужно считать устаревшими по сравнению с исследованиями Пирсона, Хьюга и Гримисона (см. стр. 185 и далее), которые проведены в большом масштабе во взаимной связи с теплоотдачей при омывании пучка труб потоком в поперечном направлении.
Потеря давления, согласно американским исследованиям, вы* ражается следующей формулой:
F • N • G2 „ /onm
, р — —-------------- дюйм вод. ст. (809)
Н 10,84 • 108 • Y
В этом уравнении:
/ — коэффициент трения, безразмерная величина;
N — число обтекаемых рядов труб;
G=y*w—массовая скорость, фунт/час фут2;
Y —удельный вес, фунт/фут3 (в данных условиях). Величина 10,84-108 содержит в себе гравитационную постоянную, благодаря чему возникает правильная размерность уравнения (809). Если уравнение (809) пересчитать в метрическую систему мер и скорости принять в м/сек, то получаем выражение, определяющее потери давления при обтекании потоком шах-
Матного или коридорного пучка труб с числом рядов N в перпе эпопен- дикулярном направлении
Д р = 0,204- /• N • Доо • то * ---- -—лшвод. ст. (818) (810)
273 • Р
Коэффициент / зависит от расположения труб. В оригина. внннале он изображен на рис. 1 и 3 в форме двух семейств кривых. Э€.. Эти кривые можно выразить формулами. Для коридорного располшнполо - жения труб приближенно получается
5пр
0,08 ~Т
, ; ;15 (818) (811)
И для шахматного расположения труб
F« =-гт==-- <818) (812)
|
I |
Из уравнения (812) следует, что потеря давления при щахмжюкмат - ном расположении труб практически не зависит от расстояншояния
Между трубами вдоль направления потока в то время к. л га как
D
При коридорном расположении потеря давления очень сильно эбожо зависит от этого расстояния. Если значения уравнения (810) пол подставить в уравнение (811), потеря давления газа в случае оэе обтекания потоком пучка труб с коридорным расположением шнем в поперечном направлении определится уравнением
|
Snp ~d~ |
|
0,0163 - м. |
|
К ' То |
|
■Ш'' |
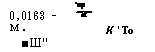 |
|
|
|
|
|
Подставляя значения уравнения (812) в уравнение (810), полшполу - чим потерю давления газа при обтекании пучка труб с шахмзмжмат - ным расположением потоком в поперечном направлении:
|
Щ • То |
![]()
|
Дрш = 0,0204-./V |
![]() Мм вод. ст. (8 8) (814)
Мм вод. ст. (8 8) (814)
В этих уравнениях;
Ар — общие потери давления в пучке, мм вод - ст.;
N — число рядов труб;
SnP — расстояние между осями труб вдоль потока газа, м; d — внешний диаметр труб, м
Sn — расстояние между осями труб в направлении, перпендикулярном потоку газа, м w0 — скорость в самом узком сечении, м/сек (0° С.
7600 мм рт. ст.);
То — удельный вес газа, кг/нмъ
Т — средняя температура газа, °К;
Р — давление, атм.
Решая уравнение (813) при помощи логарифмической линейки, необходимо учесть, что ах'ъ есть не что иное, как а Уа Поразительно, что ни в уравнении (813), ни в уравнении (814) диаметр трубы не является основной величиной, тем более, что
Он в формуле Рейера встречается в первой степени и — без-
D d
Размерны). Напротив, потеря на трение зависит лишь от осевого расстояния, выраженного через диаметры труб. Сравнение уравнений (813) и (814) с формулами Рейера показывает, что при диаметрах трубы более 20 мм последние дают заниженные значения потери давления, а при диаметрах трубы менее 15 мм — завышенные. Так, для диаметра трубы 30 мм при коридорном расположении при средних условиях имеем соотношение
А Р ПО Рейеру = о 55 Д р по Гримисону ’
И для d = 20 мм
А р по Рейеру _ q gg Д р по Гримисону ’
Уравнения (813) и (814) справедливы в области чисел Рейнольдса от 2000 до 20000, следовательно, для дымового газа и воздуха примерно доходят до значения >
W0 - d = 0,5.
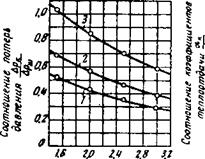
Какое же расположение (шахматное или коридорное) выгоднее, т. е. при каком расположении достигается определенный коэффициент теплоотдачи при минимальной потере давления? На рис. 67 при различных расстояниях между осями труб слева дано соотношение потерь давления для коридорного (Ар* и шахматного (Дрш) расположения, а справа — соотношение соответствующих коэффициентов теплоотдачи. Вопреки широко распространенному до сих пор мнению, этот график показывает, что при определенных условиях коридорное расположение вы
годнее шахматного. Например, по рис. 67, если продольное расстояние = 3 и - поперечное — ё й
|
= 2, коэффициенты теплоот - 0,85. Это значит, что при |
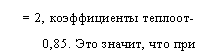 Дачи в обоих случаях равны, а Рк-
Дачи в обоих случаях равны, а Рк-
Д Рш
Коридорном расположении труб потери давления составляют лишь 85% потерь при шахматном. Лишь при малых продольных
|
(Д_ ,.5) |
![]()
|
Расстояниях |
![]() Отчетливо выявляется превосходство
Отчетливо выявляется превосходство
Коридорного расположения труб. Впрочем, общий анализ кривых подтверждает, что более низкие потери давления при определенном расстоянии дают также и более низкие значения коэффициентов теплоотдачи.
|
Рис. 67. Соотношение потери давления и коэффициентов теплоотдачи при коридорном и шахматном расположении труб: |
|
|
16 10 м 18 3.2 |
|
Относительмшш поперечный шаг А б |
 |
|
А — потеря давления; б |
![]() Коэффициенты теплоотдачи, если — равно:
Коэффициенты теплоотдачи, если — равно:
<1
1 — 1.5; 2 — 2; 5 — 3
После вывода прицеленных выше формул появилось новое исследование потерь давления в пучке труб Тер Линдена[198]. Была исследована потеря давления в случае холодного воздуха в трубном пучке, в котором до 10 (чаще 6) рядов. Этот трубный пучок был помещен в воздушном канале сечением 1100X 1100 лш2. Исследования проводились в области Яе — 10000-=- 70000 и один раз при Яе = 300000, следовательно, была рассмотрена область чисел Рейнольдса, которые лежат значительно выше практических значений. Результаты хорошо совпадают с результатами расчета по уравнениям (813) и (814)- Влияние диаметра так же,
Как и в зтихфор м у л ах, практически незаметно, и поэтому аткло - нения от результатов Рейера так же велики, как и указанные выше. Замечательно, что Тер Линден при сравнении с вышеприведенными результатами выяснил, что формулы Рейера справедливы лишь для трубы диам. 15 мм.
Числовой пример, который соответствует основной серии измерений Тер Линдена,
- = 1,69, — = 1,69, Яе = 10 ООО, N = 6 рядов
(I (I
(коридорное расположение труб), дает величину потери давления, на 12% меньшую, чем получается по уравнению (813). Соответственно, при шахматном расположении
— [199] 2,42, =* 10 ООО, — = 2,10, N = 6 рядов,
11 4
Потери давления, по данным Тер Линдена, получились на 6% меньше, чем по уравнению (814). Если учесть, что Тер Линден проводил исследования без учета влияния теплопередачи, а уравнения (813) и (814) представляют собой формулу интерполирования, то совпадение можно считать достаточно хорошим.
Несмотря на это, измерения в производственных условиях*, проведенные на большой системе труб (канальные рекуператоры), например с 30 рядами труб, расположенных коридорно друг за другом, при высоких температурах показали, что действительные потери давления в большинстве случаев на 50% больше по сравнению с высчитанными по уравнениям (813) и (814). Прежде всего возникает подозрение, что это является следствием влияния высокой температуры или состава газа, хотя это противоречило бы теории [без учета влияния вязкости при сильной турбулизации и, следовательно, сильного влияния температуры, согласно уравнениям (813) и (814)]. Чтобы объяснить эти расхождения, К. Шак * провел исследование на системе труб (квадратный канал с размером сторрны 35 см) при температурах до 900° С. Работая при стабилизированном турбулентном режиме, он подтвердил справедливость уравнений (813) и (814). Таким образом, температурное влияние точно соответствовало теории, Напротив, повышенные потери давления получались в дом случае, если газ протекал через пучок с возмущениями. В этой системе повышение составило примерно 28%.
Дальнейшие измерения были проведены на системе труб в канале квадратного сечения длиной в 1 м при шахматном и коридорном расположении труб. Газ проходил через 18 рядов труб.
Эта измерения, проведенные на успокоенном потоке при коридорном расположении труб, дали величину потери давления на 18% больше, чем получается по формулам Гримиоона. Можно предположить, что при сильно возмущенном потоке, как это чаще всего бывает на практике, повышение потерь достигает 50% по отношению к. расчетным.
При шахматном расположении труб влияние возмущений потока было гораздо меньше. В противоположность коридорному расположению при шахматном потери давления в большом канале получались даже на 15% меньше, чем по формулам Гри - мисона.
Резюмируя, можно сказать, что для больших трубных пучков результат уравнения (813) в зависимости от суммы возмущений в потоке газа необходимо увеличивать на 18-г-50%; напротив, уравнение (814) дает скорее завышенные значения.
Подобного рода увеличение потерь давления вследствие возмущений потока неожиданно, так как даже при коридорном расположении труб нужно предполагать, что поток уже позади первого ряда труб в результате отрыва вихрей возмущен так сильно, что дальнейшие возмущения никакой роли не играют. Но опыт показывает, что это не так даже при 18 рядах труб.
На основании этого объяснена по крайней мере наибольшая часть вышеназванных расхождений.
Это »серьезное влияние состояния потока проходящего воздуха было установлено также и в вентиляторах, где очень важно, будет ли поток воздуха возмущенным или нет. Даже удивительно, с какой силой идущий воздух сходит с лопастей вентиляторного колеса и приводится во вращение.
Следовательно, необходимо особое внимание обращать на начальное состояние потока газа, чего до сих пор не делалось (ср. также теплоотдачу на начальном участке, стр. 163 и далее).