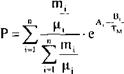ШИНЫ. НЕКОТОРЫЕ ПРОБЛЕМЫ ЭКСПЛУАТАЦИИ И ПРОИЗВОДСТВА
Математическая модель процесса десорбции многокомпонентной смеси в режиме вакуумного осциллирования
В процессе адсорбции активированный уголь, наряду с парами бензина, поглощает влагу и пары других веществ, присутствующих в составе вентиляционных выбросов. Поэтому при рассмотрении механизма десорбции следует учитывать удаление из адсорбента многокомпонентной смеси.
Процесс десорбции может быть представлен как совокупность последовательно протекающих стадий.
Первая стадия представляет собой удаление паров конденсированной в порах адсорбента смеси [530]. Испарение смеси происходит с постоянной интенсивностью в основном с поверхности адсорбента и обусловлено движением конденсированной жидкости из внутренних слоев гранул по порам за счет градиента капиллярного давления:
DU
— = cons t (58)
Dx
Где U - концентрация паров конденсированной смеси; т - время.
Для описания закономерностей процесса можно воспользоваться дифференциальным уравнением тепломассопереноса [529], преобразованным в виде:
CdT„ =U-^ri-dmj+dU-Jr.-m, (59)
I=l i=l
Образующийся пар над адсорбентом находится в равновесии с конденсированной жидкостью, имеет одинаковый состав в свободном объеме десорбера и мгновенно отводится в конденсатор. При этом скорость изменения концентрации i-ro компонента в паровой смеси определяется на основе дифференциального уравнения материального баланса простой перегонки.
Общее давление в десорбере зависит от состава удаляемой смеси паров и подчиняется закону Дальтона:
Понижение давления в десорбере осуществляется за счет отвода инертного газа вакуумным насосом и конденсации смеси паров на охлаждающих поверхностях.
Математическое описание процесса конденсации паров при отсутствии инертного газа сводится к уравнению теплового баланса:
|
11 |
|
СК) = М0 • ] и,-и)-Сяі.<ІТм-и£гіті-гіи£гіш1 , (62) |
|
Її |
|
![]()
А расчетная хладопроизводительность холодильного агрегата определяется формулой:
Вторая стадия десорбции представляет собой теплообмен в слое адсорбента при радиальной фильтрации теплоносителя [531]. Процесс десорбции понижением давления осуществляется в адиабатических условиях, при этом количество десорбирующегося пара растворителя зависит от изменения теплосодержания насыщенного адсорбента и остаточного давления в аппарате. Периодический подвод тепла к адсорбенту обеспечивает высокую скорость испарения адсорбированного растворителя. Поэтому для устранения выделения паров растворителя в окружающую среду нагрев адсорбента осуществляют конвекцией в замкнутом цикле теплоносителя [532]. Дифференци-
Альное уравнение переноса энергии для парогазовой смеси в цилиндрических координатах [533] при равномерном распределении теплоносителя в слое адсорбента записывается в виде:
|
ЭТ Qv ЭТ + v |
|
Di F■ є dR. |
|
||
|
||
А дифференциальное уравнение теплового баланса для адсорбента без учета термического сопротивления его гранул имеет вид:
|
Af |
|
(65) |
![]() (Т-Тм)
(Т-Тм)
Дт С • р0 • (l - е)
Краевые условия для системы уравнений (64), (65) можно записать как граничные условия:
T(t, Rm, M)=TH = const (66)
Начальные условия:
TM(0,Rj = TM„ (67)
|
Т(0,Яа„) = ТМи (68) Для гранул адсорбента, обладающих термическим сопротивлением, теплообмен с парогазовой смесью осуществляется в сочетании с теплопроводностью внутри самой гранулы: / |
|
Эт |
|
ЭТ |
|
М |
|
М |
|
= a |
|
(69) |
|
Д х |
|
А х |
|
Эх |
|
В этом случае краевые условия (66)-(68) дополняются граничным условием третьего рода: |
|
Ат, |
|
М |
|
X- |
|
Дх |
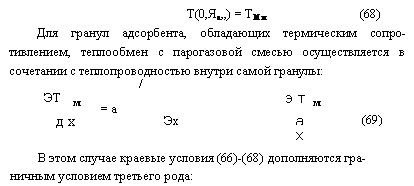 |
|
|
|
|
|
|
|
|
Х=0 |
|
(72) |
![]() Нагрев адсорбента парогазовой смесью обеспечивает перераспределение паров по сечению гранул. Начальное условие перед последующей стадией вакуумирования может быть записано аналогично формулам (67) и (68), если:
Нагрев адсорбента парогазовой смесью обеспечивает перераспределение паров по сечению гранул. Начальное условие перед последующей стадией вакуумирования может быть записано аналогично формулам (67) и (68), если:
И (0, Яап, х) = ин
![]() Третьей стадией десорбции является удаление паров из капиллярно-пористого адсорбента понижением давления во втором периоде процесса [534]. В этом процессе наблюдается постепенное углубление зоны испарения вглубь гранул. Для описания процесса тепломассопереноса можно использовать приближенное решение задачи, предложенное в [530]. Согласно этому решению распределение содержания паров и температуры для зоны испарения и зоны, содержащей пары растворителя, можно представить в следующем виде:
Третьей стадией десорбции является удаление паров из капиллярно-пористого адсорбента понижением давления во втором периоде процесса [534]. В этом процессе наблюдается постепенное углубление зоны испарения вглубь гранул. Для описания процесса тепломассопереноса можно использовать приближенное решение задачи, предложенное в [530]. Согласно этому решению распределение содержания паров и температуры для зоны испарения и зоны, содержащей пары растворителя, можно представить в следующем виде:
(73)
![]()
|
X = (х _т V-______________ 5: ММ Vі Мп 1м£,/ £ |
![]()
![]() (74)
(74)
•(иці-и5і) (75)
|
|
|
М^) (76) |
Граничные условия для системы уравнений (73)-(76) записываются по зонам: для зоны испарения:
ТМ„=Т (77)
АшНр0 г *" атНр0^)|
(78)
|
Ига = «ф, |
![]()
|
(79) |
![]() Р V*
Р V*
Р
Чгм; у
|
Т - Т Ч *Мп ч Л#1 — $ |
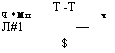 Для зоны, содержащей пары растворителя:
Для зоны, содержащей пары растворителя:
|
* (Тмц ^Мп ) |
![]() Г
Г
"ЕчШ (80)
1=1
|
А |
|
Т1| |
|
КР Р|-Ре |
|
+ |
|
Ро |
|
Тт _тт т _т 5.x Мп м$ К * у |
|
И,- - и • -Й---- —+ 5. Я., -£ |
|
= 2а |
|
Т21 |
|
|
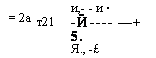 |
|
|
|
Скорость углубления поверхности испарения - 4 определяется по методике, основанной на анализе температурных кривых [530] и в общем виде может быть представлена уравнением регрессии:
^(х) = Ь0 + Ь, т + Ь2т2 + Ь3т3 +... (82)
Связь между температурой адсорбента и парциальным давлением і-го компонента на поверхности испарения определяется уравнением [534]:
/
|
(83) |
![]()
|
-в,/тМ£ У |
![]() Р5І = ехр<
Р5І = ехр<
Поток паров по і-му компоненту - }пі (т) зависит от режима работы конденсатора и может быть определен по уравнениям (62) и (63), а скорости изменения парциальных давлении компонентов - сіРі / сІт и температуры паровой смеси - сіТ / сіт по уравнению материального и теплового балансов.
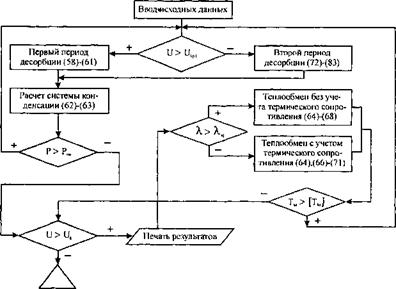
Блок схема алгоритма расчета процесса десорбции по математической модели, представленной системой уравнений (58)- (83), приведена на рисунке 75.
Расчет по этому алгоритму ведется в следующей последовательности. После ввода исходных данных, представляющих собой сведения о теплофизических характеристиках конденсированных жидкостей, паров, газа, насыщенного адсорбента и свойствах дисперсного слоя, ЭВМ проверяет условие, по которому определяется дальнейший порядок вычислительных операций. Если начальное содержание паров в адсорбенте больше содержания паров в первой критической точке (и>икр1), то расчет ведется по уравнениям (58)- (61), относящимся к первому периоду десорбции. При и<икр, расчет ведется по уравнениям (73)-(83), описывающим процесс десорбции во втором периоде. Одновременно с расчетом кинетики процесса определяются режимные параметры системы конденсации по уравнениям (62) и (63), после чего проверяется соотношение между остаточным давлением в десорбере и заданным оптимальным значением.
|
Рис. 75. Блок-схема алгоритма расчета. |
Если остаточное давление в десорбере ниже заданного, то процесс нагрева слоя адсорбента рассчитывается без учета термического сопротивления гранул (при Х>Х эф), или с его учетом.
Расчет прекращается при достижении конечного значения содержания паров растворителя в адсорбенте.
Для решения системы уравнений (58)-(83) использовались численные методы расчета.
Проверка адекватности полученной математической модели в виде уравнений (58)-(83) осуществлялась с применением лабораторной адсорбционной установки с электроконтактным подводом тепла. Полученные расчетные и экспериментальные результаты представлены на рисунке 76. Результаты статистической обработки экспериментальных и расчетных данных по-
О --------------------------------------- —-—а-‘
О 5 10 15 20 25 30 35 40 45 50 55 60 Т, МИН
Рис.76. Зависимость температуры адсорбента (Т), количества десорбированного растворителя (и) и остаточного давления (Р) от продолжительности первого периода десорбции.
По оси ординат отложены: ддд - расчетная Тр, К;
+++ - экспериментальная Тэ;
ООО - расчетная и х 500, кг/кг; ххх - экспериментальное Цх 500;
**•* - расчетное рр х 3, кПа;
Ооо - экспериментальное рэ х 3.
Казали, что разработанная математическая модель удовлетворительно описывает первый период десорбции на лабораторной установке, что свидетельствует о возможности ее использования для описания первого периода десорбции на опытнопромышленной установке.