Машиностроение ТЕХНИКА И ТЕХНОЛОГИИ

Расчетная схема и математическая модель робота

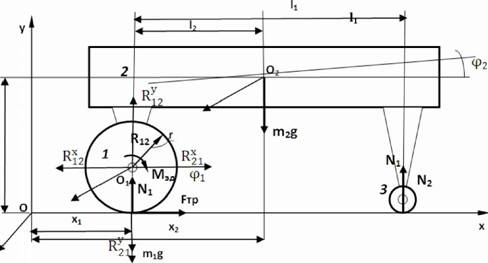
Расчетная схема робота показана на рис. 1. Рассматриваемый в работе робот движется в неподвижной системе коор­динат oxyz , причем предполагается, что робот находится все время на плоскости Oxy с координатой z=0.

Робот состоит из ведущего колеса 1, установленного на валу управляемого электродвигателя постоянного тока, ко­торый неподвижно закреплен на корпусе робота 2, и поддерживающего рояльного колеса 3. В дальнейшем принято, что элементы робота - недеформируемые твердые тела, а при взаимодействии ве­дущего колеса с шероховатой поерхно­стью возникает нормальная реакция, сила трения и момент трения качения. На ро­яльное колесо со стороны поверхности действует только нормальная реакция.

Пусть вес корпуса робота с электро­приводом и рояльным колесом приложен в точке О2 .А вес ведущего колеса прило­жен в точке О1 , являющейся геометриче­ским центром колеса.

Для построения математической мо­дели, описывающей движение робота, рассмотрим отдельно движение корпуса совместно с рояльным колесом и ведуще­го колеса. Пусть x2,y2, ф2 - обобщенные координаты, определяющие положение корпуса робота. Тогда дифференциальные уравнения, описывающие движение кор­пуса робота, можно представить в виде

M2x2 = RX2

M2 У2 =-m2g + N2 + R12

J02 ф2 = МЭД + N2(l1 -12)-RX2(l3 -Г) + R12l2

Где m2,J02 - масса и момент инерции корпуса робота; m1- масса ведущего ко-

Леса; Rf2

12 - проекции силы, дейст­вующей со стороны колеса на корпус, N2 - нормальная реакция; l1, 12 - геометриче­ские размеры корпуса; r - радиус колеса; Мэд - момент, действующий на корпус со стороны электродвигателя.

Пусть x1, y1 , ф1 - обобщенные коор­динаты, определяющие положение веду­щего колеса.

Дифференциальные уравнения дви­жения колеса робота с учетом свойств управляемого электропривода примут вид

Ld + iR + сю (Р1 = U(t) dt

M1 Х1 = RX1 + F-П m1 У1 = Ry1 + N1

J01 ф1 =- N15 + Мэд + ф.

При этом предполагаем, что ф1 не

Равно нулю.

Здесь обозначено: L, R - индуктив­ность и активное сопротивление якоря электродвигателя; сю - постоянная элек - угловая скорость колеса; N1,Fj!^- нор-

Мальная реакция и сила трения, дейст­вующие на колесо со стороны опорной поверхности; Ry1, R^ - силы, дейст­вующие на колесо со стороны корпуса; x1, y1 , ф1 - обобщенные координаты, опре­деляющие положение колеса; 5-коэф - фициент трения качения.

Будем считать, что момент электро­двигателя зависит от тока якоря по сле­дующему закону:

Myi = Mya (i) =

.dM^ (8)

+ i3^^^^)3 +... di di

Ограничим этот ряд только вторым и третьим слагаемыми, то есть

Mya = 1 • C1e +13 • C3e,

Где^ C1e, C3e - экспериментально опре­деляемые постоянные.

На первом этапе будем считать, что проскальзывание ведущего колеса по ше­роховатой поверхности отсутствует, кро­ме этого, колесо и опорная точка не от­рываются от поверхности, то есть N1 > 0

N>0, тогда можно записать следующие уравнения связей:

TOC o "1-3" h z ф1г = x1. (9)

У1 =r. (10)

X2 = x1 +12 , У2 = l3 , ф2 = (11)

Запишем также очевидные равенства:

(12) (13)

Анализируя уравнения (1),(5),(7) в

Начальный момент времени, когда ф1 = 0 , с учетом условий (9)-(13) запишем сле­дующее выражение, определяющее ко­эффициент трения качения в покое: 51 = Mya / N1.

Если коэффициент трения качения 51 меньше предельного 5 , то есть

51 = Mya / N1, (14)

Вращение колеса не происходит, и робот стоит на месте.

Только при выполнении равенства 51 = 5 (15)

Начинается движение.

Задача исследования динамических закономерностей пускового режима ро­бота может быть сформулирована сле­дующим образом. Пусть дано: m1, m2, l1, І2, І3, r, 5, J01Z, J02Z. L, R,croc1e2c3e.

Решая уравнения (1)-(7), с учетом условий (8)-(15) необходимо определить

Неизвестные: x1, y1, x2, y2, ф1, ф2, N1, N1, FsiE), Rx2, R|1, R12, Ry1, i, Mya для различных за­конов управляющего напряжения U(t).

Рассмотрим различные способы управляемого пускового режима. На рис.2 приведен график зависимости на­пряжения питания, поступающего на об­мотки якоря электродвигателя, от време­ни [6-9].

Кусочно-постоянный 2-этапный ал­горитм управления.

Данный алгоритм характеризуется 4- мя параметрами U1, U2, t, t2, изменение которых влияет на разгон робота. Преоб-

U, B

Разуем систему уравнений (1)-(7) с уче­том условий (8)-(15) к виду

Ld + iR + сшср1 = U(t) dt

(m1 + m1)g = N1 + N2

J01 ф1 =-N15+ ic1e -

-(m1 + m1)r2 ф1 0 = ic1e + N2 (I1 -12) -

-m2r ф1 (13 - r) - (N1 - m1g)12.

Система уравнений (16)-(19) имеет 4 неизвестных ф1, N1, N2,i

Из (18) найдем нормальную реакцию N1:

N1 = (ic1e - (m1 + m2)r2 ф1- J01 ф1)/-5

Подставив это выражение в (17), по­лучим

(m1 + m1)g =

= (ic1e - (m1 + m2)r2 ф1- J01 ф1)/ 5 + N2.

Отсюда определим величину реак­ции N2 в виде

N2 = (m1 + m1)g -

(iC1e - (m1 + m2)r2 ф1 - J01 ф1)

5

Из уравнения (19) найдем:

M2r2 ф1(13 - r) =

= ic1e + N2(11 -12) - (N1 - m1g)12.

U2

U1

T, c

Рис.2. Зависимость управляющего напряжения от времени

Ток для нахождения момента элек­тродвигателя найдем из уравнения пол­ного тока:

Ld + iR + cffl(Pl = U(t). dt

Таким образом, уравнения имеют три неизвестных: (j, N2,i.

Подставляя переменные, получим следующее:

[J02 + (m1 + m2)r2] ф = 1 (21) = [-(m1 + m2)g + - (m2gl2 - ic1e)]5 + ic1e. i1

TOC o "1-3" h z Ld + iR + cro((1 = U(t). (22)

Dt

Обозначим общую массу робота m: m1 + m2 = m, (23)

А J - приведенный момент инерции:

J = J01 + (m1 + m2)r2. (24

Тогда уравнение (22) принимает вид

J(1 = [m2gг - mg - —]§ + ic1e 11 i1

Или

I * S

J(1 = (m2gf - mg)5 + i(c1e - ic1e-). (25)

II 11

Величина коэффициента трения ка­чения - значительно меньше длины 12, тогда приближенно можно считать, что

- = в« 0. 1

Примем следующие обозначения:

12

A = M2Gf - mg. 11

Тогда с учетом (27) уравнение (25)

Запишем в виде

JcP1 = A-+i(c1e - c1e-);

11

Ldi + iR + cro((1 = U(t). dt

Система дифференциальных уравне­ний (28)-(29) содержит две неизвестные величины ф1, i, определив которые можно найти зависимости всех параметров оп­ределяющих пусковой режим робота. За­давая различные законы управляющего напряжения, можно изучить закономер­ности пускового режима робота при от­сутствии проскальзывания для любого закона управляющего напряжения. Полу­ченные формулы позволяют изучать про­цесс запуска колесного робота из любых начальных условий, в том числе и нуле­вых, для различных стратегий управле­ния. Наиболее удобной средой для вы­полнения вычисления является вычисли­тельный пакет MATLAB SIMULINK.