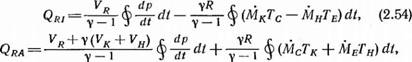Регенератор
Регенератор обычно изготавливается из пористого материала, образующего длинный извилистый канал для протекающего по нему рабочего тела, чтобы обеспечить наибольшую площадь поверхности контакта между материалом регенератора и газом. Высокие значения суммарного коэффициента теплоотдачи в регенераторе достигаются не только за счет развитых теплообмен - ных поверхностей, но и за счет малых гидравлических диаметров. Эти факторы обеспечивают близкую к единице «эффективность» регенеративных теплообменников при условии, что теплоемкость материала существенно больше теплоемкости рабочего тела. Это условие в общем ограничивает использование регенераторов случаем систем с газообразным рабочим телом. Регенераторы используются на различных крупных предприятиях типа доменных и стеклоплавильных печей, а также на газотурбинных станциях. Эти регенераторы обычно представляют собой крупные теплообменники, размеры которых достигают 40 м и в которых направление потока не меняется в течение периодов, составляющих многие часы. Регенераторы, применяющиеся в современных двигателях Стирлинга, считаются большими, если их диаметр превышает 60 мм, а периоды движения потока в одном направлении составляют несколько миллисекунд. Поэтому большая часть подробных аналитических результатов, полученных для крупных инерционных регенераторов, вряд ли применима для регенераторов двигателя Стирлинга, хотя основные концепции и принципы работы являются, по существу, одинаковыми. В регенераторах малого размера гораздо большее значение имеют такие факторы, как аэродинамическое сопротивление, влияние стенки кожуха регенератора и «задержка» рабочего тела. Последний эффект вызван тем, что некоторая часть рабочего тела не может пройти весь канал регенератора и «задерживается» внутри него на несколько циклов вследствие сложности природы колеблющегося и возвратного течения, а это отрицательно влияет на характеристики теплообмена в регенераторе.
Такие же сложные проблемы возникают при анализе термодинамических характеристик двигателя Стирлинга, но, как мы видели, рассмотрение идеального цикла помогает понять влияние основных факторов и их взаимосвязи. Более того, применение такой тактики исследования позволяет оценить практическую осуществимость теоретических концепций и понять, по
чему нужно выбрать данную конструкцию или принять данные теоретические положения. Основные требования к регенератору определяются термодинамическими процессами идеального цикла, а практическая конструкция в значительной степени диктуется термодинамическими процессами, преобладающими в реальных двигательных системах. Следовательно, наиболее разумно начать наше краткое описание теплообмена в регенераторе и принципов, определяющих работу регенератора, с анализа идеального цикла.
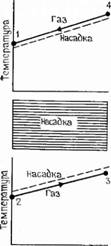
Рассмотрим диаграммы состояния идеального цикла, приведенные на рис. 1.15. Как показал термодинамический анализ, чтобы получить КПД двигателя Карно, тепло, выделенное в изохорном процессе 4— 1, должно быть возвращено газу в изохорном процессе 2—3. В идеальном случае такой перенос тепла можно осуществить обратимым образом с помощью регенератора. Принцип работы этого теплообменника иллюстрируется на рис. 2.19. По длине реге нератора поддерживается постоянный градиент температуры, т. е. температура изменяется ЛИНеИНО ОТ 1 max ДО 1 min. Рабочее тело входит в регенератор в термодинамическом состоянии 4, передает свою избыточ ную энергию материалу регенератора и выходит из него в состоянии 1. В течение этого процесса, называемого «периодом горячей продувки», температура каждого элемента регенератора повышается на беско нечно малую величину. После завершения процесса сжатия рабочее тело, находящееся теперь в состоянии 2 при минимальной температуре цикла, вновь пропускается через регенератор и забирает тепло, запасенное при горячей продувке. При этом температура каждого элемента регенератора снижается на бесконечно малую величину, а рабочее тело после такого «периода холодной продувки» выходит из регенератора в состоянии 3, т. е. при максимальной температуре цикла.
|
Рассптояние Рис. 2.19. Принцип работы регенератора двигателя Стирлинга |
Чтобы весь процесс теплообмена был обратим, разность температур между рабочим телом и материалом регенератора в любой момент времени должна быть бесконечно малой. Для выполнения этого требования нужно удовлетворить некоторым условиям. Во-первых, процесс будет обратимым лишь в том случае, если в любой момент времени достигается термодинамическое равновесие, т. е. система регенератора в периоды движения потока должна проходить через ряд равновесных состоя
ний (называемых иногда квазистатическими) [27]. Это можно гарантировать лишь в том случае, если процесс протекает бесконечно медленно. Такое условие никогда не выполняется на практике, особенно в двигателе Стирлинга, в котором массовые скорости очень велики, а скорость вращения вала достигает не скольких тысяч-оборотов в минуту. Следовательно, нужно обязательно удовлетворить оставшимся условиям, которые можно без труда определить из основных уравнений, описывающих динамические характеристики регенератора. Эти уравнения были получены Нуссельтом и Хаусеном [28]. Уравнения, опи сывающие перенос тепла от рабочего тела к насадке, установленной в канале регенератора, получены на основании баланса энергии. Рассмотрим вначале рабочее тело
1'су. А (Тм - 7» = MFCpFLR (dTF/dx) -F MFRC„ (dTF/dt). (2.43)
(Полный список обозначений приведен в конце этой главы.)
Правая часть уравнения (2.43) выражает тепловую энергию, подводимую к рабочему телу. Разность температур насадки и рабочего тела Тм — TF в левой части уравнения должна быть бесконечно малой, и, как показано в гл. 1 (рис. 1.104), количество дополнительной энергии, подведенной к рабочему телу, и скорость выделения тепла должны быть чрезвычайно высокими. Следовательно, суммарный коэффициент теплоотдачи Лсум должен быть бесконечно большим, чтобы компенсировать малую разность температур. Опять-таки это условие на практике недостижимо, хотя при проектировании можно предпринять некоторые меры, чтобы получить возможно больший коэффициент теплоотдачи в пределах ограничений, предъявляемых к конструкции всей системы. Остается единственный параметр — площадь теплообменной поверхности, которая должна быть бесконечно большой, чтобы приблизиться к идеальным условиям. Очевидно, это также физически недостижимо, но нужно всеми способами стремиться увеличить площадь этой поверхности. Практическим способом увеличения площади поверхности при заданной массе материала регенератора является применение проволок или небольших частиц, ориентированных таким образом, чтобы сделать проходной канал максимально извилистым.
Второе уравнение Нуссельта — Хаусена выражает способность регенератора аккумулировать энергию:
HcyMA (TF - Тм) = ММСРМ (<dTJdt), (2.44)
Где теплоемкость регенератора Ск определяется членом МмСрм, Который представляет собой произведение массы на удельную теплоемкость материала регенератора. На основании предыдущих соображений величина СR должна быть бесконечно большой или равной нулю, чтобы удовлетворить заданным требованиям, если ЛСум или А бесконечно велики, иначе разность Tf — Тм не будет бесконечно малой. Это справедливо, разумеется, в том случае, если сама производная DTM/Dt бесконечно мала. Но каким еще условиям надо удовлетворить, чтобы эта производная была бесконечно малой? Некоторые результаты можно получить, приравнивая (2.43) и (2.44) и учитывая обычное условие для знака теплового потока. Тогда в первом приближении получаем
ATM~MFCpFATF/CH (2.45)
И, следовательно, чтобы значения АТм, т. е. изменения температуры насадки регенератора, были минимальными, нужно минимизировать отношение теплоемкостей рабочего тела и материала регенератора. Более того, для поддержания требуемой разности температур вдоль регенератора необходимо, чтобы кондуктивный перенос тепла в осевом направлении отсутствовал, а по нормали к потоку был максимальным; при выполнении этих условий температура в каждом сечении канала постоянна по ширине насадки. Таким образом, для идеальной регенерации требуется выполнение нескольких почти абсолютно невозможных физических условий.
Проблема еще больше усложняется, если учесть реальные термодинамические и газодинамические характеристики процессов в двигателе Стирлинга. Температуры рабочего тела, выходящего пз рабочих полостей переменного объема, не постоянны (т. е. изотермические условия не достигаются), поскольку процессы являются, по существу, адиабатными. Даже в тех условиях, когда рабочее тело течет в нагревателе и холодильнике по трубкам, наружная поверхность которых поддерживается практически при постоянной температуре, температуры рабочего тела на концах регенератора будут периодически изменяться по времени и возможны даже отдельные моменты, когда либо течение отсутствует, либо создаются встречные потоки, либо газ в одно и то же время вытекает с обоих концов регенератора [29]. Площадь теплообменной поверхности не бесконечна, а газодинамические характеристики и теглофизические свойства рабочего тепа (плотность, давление, скорость, вязкость) переменны; происходит кондуктивный перенос тепла в осевом направлении, аналогичный перенос по нормали к потоку не является идеальным и т. д. Чрезвычайно сложно даже качественно разобраться в реальной ситуации, не говоря уже о том, чтобы провести расчет.
Поскольку регенератор является весьма специфичным теплообменником, для него должно быть проведено значительно больше экспериментальных исследований теплообмена, чем для двух других теплообменных устройств. Однако лишь в последнее время начались интенсивные аналитические исследования, поскольку были разработаны и созданы очень простые и очень эффективные регенераторы, в то время как вначале основные усилия были направлены на создание работающего двигателя, а теорией регенератора явно пренебрегали, по крайней мере не публиковали никаких результатов. Теперь же, когда двигатели доказали свою жизнеспособность, нужно конструировать двигатели самых различных размеров, причем необходимо снизить пропорционально возрастающую стоимость регенераторов и исследовать их новые типы. Легче и удобнее с точки зрения затрат времени и средств изучать соответствующие проблемы с помощью ЭВМ, а не полагаться только на эмпирические данные. Однако для проведения численных расчетов необходимо иметь надежную и обоснованную аналитическую базу, а она еще только создается. Достижениям в этой области можно посвятить много страниц, насыщенных математическими выкладками, но обсуждение этих исследований выходит за рамки нашей книги. Тем не менее, поскольку большинство читателей знакомо в основном с трубчатыми теплообменниками, а не сетчатыми регенераторами, мы изложим основные понятия на современном уровне знаний, заостряя внимание на терминологии, относящейся к регенераторам. Это позволит подчеркнуть сложность проблемы и яснее показать необходимость продолжения исследований.
Регенератор, бесспорно, является самым важным теплообменником системы двигателя Стирлинга, поскольку, хотя двигатель может функционировать и без регенератора, преимущества работы по замкнутому циклу нельзя реализовать без эффективного регенеративного теплообменника. Как мы уже видели, для эффективной работы регенератора нужно найти компромисс между несколькими противоречивыми требованиями. Очевидно, было бы полезно знать, насколько точно можно выполнить самые доступные компромиссные условия. В качестве первого шага определим наиболее важный параметр — эффективность регенератора. Несколько спорное, но вполне приемлемое определение эффективности Er выглядит следующим образом:
Действительно перенесенное количество тепла, С)
R Количество тепла, которое можно было бы перенести
Чтобы выразить eR через измеряемые параметры, можно, следуя Типплеру [30], воспользоваться соотношениями (2.43) и (2.44). Эти соотношения можно записать через безразмерный параметр времени г] и безразмерную координату получая в результате [31]
DTF№ = TM-TF, (2.47)
ДТц, Щ = ТР-Тм, (2.48)
Где Z = hcyMAx/(MFCpFLR), (2.49)
11 = [ЛсуА'ШмСрм)] [т - MFRxl(MFLR)]. (2.50)
Величина т — это период времени рассматриваемой продувки. Хаусен [31] предложил еще два безразмерных параметра для каждого периода продувки, связанных с ^ и г], которые стали двумя основными характеристиками в теории регенератора, а именно приведенную длину Л и приведенный период П:
Л = Асу ЛШРСрР), (2.51)
П = [hcyMA/(MMCpM)} (т - MFR/MF), (2.52)
Причем эти величины содержат параметры, для которых нужно найти компромисс, чтобы добиться близкой к идеальной работы регенератора. С помощью параметров Л и П можно найти выражение для эффективности [30]:
=irth л + 2 ' 12-53>
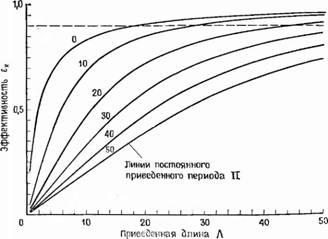
Где параметр П определяется без учета задержки газа в регенераторе, т. е. при MFR = 0. При некоторых условиях течения это предположение может стать несправедливым. Полезным является и параметр П/Л, называемый коэффициентом использования [11], поскольку он представляет собой отношение теплоемкости рабочего тела в период продувки к теплоемкости насадки. На рис. 2.20 представлены данные, показывающие зависимость ER от Л и П, причем желательной областью работы для двигателя Стирлинга является зона над штриховой линией. Хотя такой подход позволяет получить некоторую информацию о том, к какому компромиссу между различными факторами следует стремиться, разработка удовлетворительного регенератора является конструкторской, а не расчетной задачей. Однако для использования этого подхода при проектировании регенератора недостает двух важных величин — суммарного коэффициента теплоотдачи и массового расхода газа. В настоящее время ввиду нестационарного характера течения невозможно получить аналитическое соотношение для расчета /гсум.
Поэтому были использованы эмпирические данные, но для условий течения, характерных для двигателя Стирлинга, их имеется очень мало. Вопрос об использовании экспериментальных данных будет рассмотрен в следующей главе. Массовый расход газа изменяется в течение периодов продувки, поэтому следует до некоторой степени произвольно решить, какую величину выбрать для использования в расчетах, т. е. минимальную, максимальную, среднюю, среднеквадратичную или какую - либо иную. И опять этот вопрос относится скорее к стадии конструирования. Таким образом, даже при использовании упрощенной математической модели возникают трудности в ее интерпретации. Ясно, что теория обычного регенератора действительно может оказаться полезной при определении основных
|
Рис. 2.20. Изменение эффективности регенератора. (Результаты расчета по формуле Типплера [301.) |
Закономерностей и, как будет показано, полезна при разработке конструкции, но тем не менее она не дает возможности рассчитать характеристики регенераторов, работающих в циклических машинах типа двигателя Стирлинга, без введения некоторых усовершенствований и включения в уравнения члена аккумулирования газа Mfr. Последний фактор вызывает так называемую задержку в регенераторе. Ввиду очень быстрого изменения направления течения в регенераторе двигателя Стирлинга весьма вероятно, что лишь некоторая часть всего газа проходит через насадку, и эта часть может быть меньше той, которая задерживается в насадке. Было показано [11, 15], что часть рабочего газа вообще не проходит полностью через насадку, а другая часть никогда не выходит из регенератора. Поиск строгих аналитических решений еще продолжается [16, 32]. Тейлор и Эванс [33] обобщили метод Харнесса, и можно надеяться, что подробные результаты их исследования вскоре бу-
17 Зак. 839
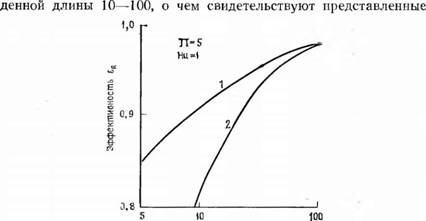
Дут опубликованы. Это исследование посвящено в основном уточнению численного расчета и моделирования, однако оно основано, по существу, на соотношениях (2.43) и (2.44). Результаты работы Харнесса и Ньюмана [16] показывают, что расчет по обычной теории дает заниженные значения эффективности регенератора, работающего в условиях периодически изменяющегося течения. Действительно, влияние задержки рабочего тела проявляется особенно сильно при значениях приве-
|
Приеейенная Ьлин& Л Рис. 2.21. Влияние задержки рабочего тела на эффективность регенератора [16]. 1—с задержкой; 2—без задержки. |
На рис. 2.21 данные для случая относительной массы задержанного газа Ни=1, т. е. когда масса газа, содержащегося в регенераторе, равна массе газа, прошедшего через него в течение одного периода продувки. Кроме того, при обычном подходе, как правило, предполагается, что периоды продувки одинаковы (это условие известно под названием «сбалансированная регенерация»), и иногда принимается, что эффективность постоянна. В двигателе Стирлинга эти условия не выполняются [16, 34].
До сих пор рассматривались условия для идеальной регенерации, а в первой части главы при анализе основных термодинамических характеристик было наглядно показано влияние отклонений от идеального случая. Если регенератор работает идеально, то суммарный перенос тепла в течение одного цикла равен нулю, и поэтому еще одной характеристикой работы регенератора является Qr — количество тепла, перенесенное за цикл. Выражение для QR, как и для других критериев работы, можно найти, применяя аналитические соотношения для идеального случая. Их можно получить как на основании чисто термодинамических соображений, так и рассматривая теплообмен при течении газа. Если применяется термодинамический подход, то следует учесть оба предельных случая, когда рабочий объем изменяется по изотермическому пли по адиабатному закону.
Какой бы подход ни применялся, основной принцип остается неизменным: чтобы найти выражение для QR, нужно вычислить поток энтальпии в течение одного цикла. Этот анализ не очень сложен, но требует проведения довольно трудоемких математических операций. В работе Берчовица [1] дается полное описание расчета QR при использовании термодинамического подхода; мы же приведем лишь итоговые соотношения для величин Qri и Qra, соответствующих изотермическому и адиабатному процессам:
|
(2.55) |
Где Vr,K,H — объемы регенератора, холодильника, нагревателя, соответственно; Тс, е,к, н— температуры в полостях сжатия, расширения, холодильника, нагревателя, соответственно; Мс, е— массовые расходы при сжатии, расширении, соответственно; Мк — массовый расход в направлении от холодильника к регенератору; Мн — массовый расход в направлении от регенератора к нагревателю.
В гл. 3 приведено соотношение для QRi, выраженное через основные физические параметры двигателя для случая движения кривошипа по простому гармоническому закону. Эти просто выведенные соотношения содержат важную концепцию: поскольку, по существу, следует рассматривать плотность потока энтальпии, a H = и + Pv = СРТ, можно полагать, что количество тепла, перенесенное за время цикла, выражается формулой
QR = —у § (М«тс ~ МНТЕ) dt,
Справедливой для изобарного процесса, но, поскольку давление в двигателе Стирлинга переменно, в соотношение входят дополнительные члены. Следовательно, пульсации давления в регенераторе могут ухудшить его работу по сравнению с идеальным случаем. «Изотермическая» величина Qr для всего цикла всегда должна быть равной нулю, поскольку она получена в предположении об идеальной работе, но ее последовательный расчет в ходе цикла позволяет найтн тепловые нагрузки на регенератор и определить также периодический характер этих нагрузок. В случае адиабатного процесса величина Qr также должна быть равной нулю, и этот факт можно использовать в термодинамическом анализе как показатель того, что в анализе достигнуто равновесие, т. е. если величина Qr не равна нулю, то, следовательно, еще не достигнута сходимость решения основных уравнений и требуется вновь применить итерационный метод. Для более точных математических моделей, учитывающих все происходящие процессы, величина QR также является важным параметром, так как если член Qr начинает периодически изменяться, то решение дает дополнительную информацию о работе регенератора. Лишь более совершенный анализ позволяет получить численные результаты. Однако этот простои подход показал, что изменение давления в двигателе может привести к дополнительным отклонениям от идеальной регенерации. Такой эффект может быть очень важен для более глубокого понимания действия регенератора двигателя Стирлинга, и поэтому требуется проведение дальнейших исследований, особенно если принять во внимание результаты работы Хиклинга [34], полученные в 1966 г., хотя и опубликованные в открытой печати лишь в конце 70-х годов. Хиклинг вывел соотношение для QR С помощью иного подхода, а именно рассматривая гидродинамические особенности задачи. При использовании этого подхода соотношение для Qr было найдено на основании предположения, что характеристики потока можно описать с помощью закона Дарси для течения в пористой среде [35] и законов для идеального газа:
= Hl~(Y + 1) §(Лр) Рам йи (2-56)
Где АР — падение давления в регенераторе; рлм — среднеарифметическое значение давлений на концах регенератора; б — проницаемость насадки; р—вязкость газа.
В то время когда было получено это соотношение, не существовало экспериментальных средств, которые позволили бы проверить его путем непосредственных измерений. Теперь положение изменилось.
Из соотношения (2.56) следует, что в отсутствие перепада давления в регенераторе величина Qr равна нулю и процесс регенерации протекает идеально. Однако при Еыводе этого соотношения были использованы некоторые упрощающие предположения, означавшие, что влиянием изменения давления за время цикла пренебрегалось. Следовательно, соотношение Хиклинга [34] для Qr выражает просто плотность потока энтальпии, в то время как формулы Берчовица являются полными соотношениями для переноса тепла за время цикла.
Итак, можно установить принципы работы регенератора, т. е. взаимосвязь между теплообменом, теплоемкостью и эффективностью, применяя модифицированные формы соотношений Нуссельта — Хаусена. Для реального двигателя с помощью этих соотношений можно определить условия идеальной регенерации и причины отклонения от этих условий, имеющие двоякий характер, а именно неидеальность теплообмена между газом и насадкой и конечную теплоемкость насадки. Первое означает, что бесконечно малые перепады температур не реализуются, т. е. температура газа не совпадает с температурой насадки, и в итоге газ не достигает ни требуемой степени предварительного охлаждения, нн требуемой степени предварительного нагрева. Второе приводит к тому, что и градиент температуры вдоль регенератора, и температура в любой точке регенератора не будут постоянны по времени, а будут изменяться. Это приведет к тому же результату, что и нендеальность теплообмена. Применяя соотношение Типплера [30] и характеристические параметры Л и П, можно найти требуемый уровень эффективности, хотя, как показано Харнессом и Ньюманом [16], эта величина эффективности определяется не вполне точно. Расчетные результаты Берчовица и Хпклинга показали, что прп определении эффективности регенератора важную роль играют и другие процессы, в особенности изменение давления в цикле и падение давления в регенераторе.
В этой главе теплообмен в регенераторе рассматривался в какой-то степени изолированно от других факторов, связанных как с работой регенератора, так и с действием двигателя в целом. В частности, не рассматривалось сколько-нибудь подробно влияние газодинамического трения. Это объясняется в основном тем, что, хотя упомянутые факторы, как отмечалось в гл. 1, имеют очень важное значение, они не вносят существенного вклада в понимание тепловых характеристик работы регенератора. Они более важны при разработке конструкции, когда влияние трения нужно совместить с требованиями, необходимыми для достижения высоких степеней эффективности. Как будет показано в гл. 3, такой баланс не всегда легко достигается и, более того, не все требования к теплообмену с точки зрения физической конструкции согласуются друг с другом. Выбор материала регенератора, как указано в гл. 4, также довольно сложен, особенно если дополнительно учесть такие факторы, как технологичность материала, его стоимость, срок службы и т. д. В общем ясно, что можно создать регенератор, обладающий высокой эффективностью, если имеются экспериментальные данные, но получить их — задача, требующая непропорционально больших затрат.