СИСТЕМЫ СОЛНЕЧНОГО ТЕПЛОИ ХЛАДОСНАБЖЕНИЯ

РАСЧЕТ СОЛНЕЧНОЙ РАДИАЦИИ, ПАДАЮЩЕЙ НА КОЛЛЕКТОР

Наиболее широко распространенные в настоящее время в системах солнечного тепло - и хладоснабжения плоские коллекторы устанавли­вают неподвижно и в силу этого их производительность связана как с суточным изменением интенсивности солнечной радиации, так и с их пространственным положением.

В Справочнике по климату СССР наиболее подробно приведены данные об интенсивности солнечной радиации, приходящейся на горизонтальную поверхность.

Интенсивность (плотность) потока падающей солнечной радиации для любого пространственного положения солнечного коллектора и каждого часа светового дня определяют по формуле

Ws+Vd. (6.1)

Где 1$ — интенсивность (плотном^ потока прямой солнечной радиации, падающей на горизонтальную поверхность, Вт/м ; ID — интенсивность (плотность) потока диффузной

Ч

(рассеянной) солнечной радиации, падающей на горизонтальную поверхность, Вт/м ; Р» - коэффициенты положения солнечного коллектора для прямой и диффузной (рассеянной) радиации соответственно.

Коэффициенты положения солнечного коллектора определяют по формулам:

PD = cos2 j»/2; (6-2)

Jps = cos i/sinh;

Где Ji — угол наклона солнечного коллектора к горизонту;

£ — угол падения солнечного луча на поверхность коллектора; ft — угол высоты солнца над горизонтом.

Уравнения для нахождения Ps как функции широты местности У, угла наклона коллектора J>, его азимута А, склонения Солнца & и времени Г достаточно громоздки, и их расчеты выполняют на ЭВМ. Оптимальные углы наклона коллекторов определяются периодом работы и для южной ориентации равны: для круглогодичных устано­вок fi= для летних р = ? - 15° и для работающих в отопительный период - ji = >"+ 15°.

При инженерных расчетах, не использующих ЭВМ, необходимо располагать ежечасными значениями JPS, Что приводит к резкому увеличению объема требуемой для расчета информации. В связи с этим, учитывая, что коэффициент пропускания стекла практически постоянен при угле падения луча меньше 55°С, а затем резко падает, сводя к минимуму количество поглощенной коллектором радиации, представляется целесообразным определить среднее значение Ps за этот период. Сравнение результатов такого расчета с точным показало, что расхождения не превышают 35 %.

Вычисленные на ЭВМ для всех месяцев и усредненные значения Ps для оптимальных углов наклона коллектора и вертикали в диапазоне северных широт 40 ... 60° приведены в прил. 3. При произвольном расположении коллекторов, как показали расчеты, для углов наклона Jb = У ± 15° отклонение от южной ориентации до 10° изменяет суммар­ный годовой поток падающей солнечной радиации не более чем на 5 %, до 20° - на 10 %, до 30° - на 15 %.

Эти расчеты выполнены для идеальных условий - полного отсутст­вия облачности. В действительности, почти в каждой местности наблю­дается суточная асимметрия хода и интенсивности солнечной радиа­ции. Принимая во внимание это, а также суточную неравномерность графиков нагрузки горячего водоснабжения и тепловую инерцион - 144 Ность зданий, можно допустить отклонения коллекторов к востоку до 20° и к западу до 30° с учетом влияния этих отклонений на qz.

Приведенную интенсивность (плотность) потока поглощенной солнечной радиации q ^ определяют по формуле

4Q<C - W. Q^+PU&^D), (6.4)

Где 9S и &D — приведенные оптические характеристики (поглощательная способность) солнечного коллектора соответственно для прямой и рассеянной солнечной радиации; 0,96 — понижающий коэффициент, учитывающий влияние запыпения и затененности

Коллектора.

При проектировании установок солнечного теплоснабжения очень часто коллекторы размещают отдельными секциями на плоскости, в ряде случаев ограниченной (например, на плоской крыше здания), где возможно затенение коллекторами друг друга. В этом случае на оптимизацию количества получаемой теплоты влияют два фактора: максимизация времени облучения каждого ряда за счет увеличения расстояния между ними и уменьшения их общего числа; увеличения числа рядов за счет их более плотного размещения с одновременным снижением количества теплоты, вырабатываемой каждым рядом коллекторов в отдельности.

Расстояние между рядами коллекторов можно выразить через угол ^ , под которым падает на плоскость луч, проходящий через верхнюю точку предыдущего ряда в нижнюю точку следующего. Величина tgi) определяет отношение высоты ряда к расстоянию между рядами.

Если длина коллектора / и он расположен под углом р к горизонту, то расстояние между рядами коллекторов

, = (6.5)

По сравнению с вариантом, в котором коллекторы находятся в одной плоскости, их расположение под углом и рядами требует гори­зонтальной поверхности в т раз большей площади, где

M = l + tg>3 ng-0. (6.6)

Целесообразно ввести и определить значение так называемого "фактора заполнения" /зап, позволяющего найти суммарную площадь коллекторов, которые можно подобным образом расположить на плоскости:

F А ■__________________ 1_______

Зап" F cosjft (1 + tgj? ctg V ) ' (6,7)

Где F — площадь размещения коллекторов; А — суммарная площадь коллекторов.

622—10 145

При расположении коллекторов рядами общее количество теплоты, получаемой коллектором, складывается из теплоты, полученной во время частичной и полной экспозиций его поверхности.

Высоту солнца, при которой начинается полная экспозиция коллек­тора, находят из выражения

Tgh0 = tg>> cos(A - л ). (6.8)

Если высота и азимут Солнца таковы, что коллектор освещается частично, то длину освещенной части /осв можно легко найти по высоте Солнца и расстоянию между рядами:

(ctfif )------------------------------------------------------------------- (69)

'«» (ctg/5+ctg/.)

Теперь, зная площади, можно найти плотность потока падающей солнечной радиации.

Интенсивность (плотность) потока прямой солнечной радиации определяют с учетом изменения экспонируемой площади поверхности коллектора, а плотность потока рассеянной радиации будет иным вследствие уменьшения телесного угла, в котором коллектор "видит" небесную сферу. Это значит меняется по длине коллектора и в среднем составляет:

/D3ai = /D(1 + cos,> +2cos^e )/4. (6.10)

По приведенным выражениям можно вычислить суммарное количес­тво теплоты, падающей и поглощаемой коллектором за различные периоды года, их удельные величины, отнесенные к площади поверх­ности размещения, и тем самым сравнить и оптимизировать различные варианты расстановки.

В связи с большим объемом и трудоемкостью вычислений по приве­денным выражениям разработан алгоритм и составлена программа для расчета на ЭВМ. Расчеты проводили для коллекторов южной ориента­ции на широтах 47 ... 50° с углами наклона, изменяющимися от гори­зонтального к вертикальному через 10°, с шагом рядов 7,5° задавае­мым углом V = 0° ... 90 ос. Результаты расчетов показывают, что до

= 22,5° для всех углов наклона коллекторов во все месяцы есть часы их полного облучения. Затенение рядами друг друга начинает сказываться летом при т? = 35° (расстояние между рядами меньше 1,2 их высоты), а для круглогодичных систем - при т? = 25° (расстояние между рядами меньше 1,8 ... 2 их высоты).

При расчете плотности потока солнечной радиации, поглощенной

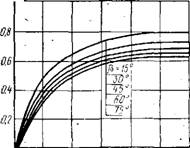
'Рис. 6.1. График зависимости "фактора ЬаЛезат незатеняемости" от расстАновКи коллек­торов

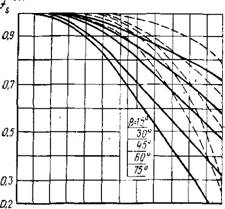
Рис. 6Л. График зависимости произведения /зап и /незат 01 расстановки коллекторов

Затеняемыми коллекторами, вводят некий обобщенный показатель плотности их размещения на плоскости, который может быть опреде­лен как фактор незатеняемости. Он показывает уменьшение радиации, которую получает затененный коллектор, расположенный данным образом, по сравнению с незатеняемым:

4незат ®пад ^зат^пад,

W (?пад — плотность потока, падающего на поверхность незатеняемого коллектора; (?зат — то же, приходящегося на затененную часть.

Значение /5Неза1 находится между 1 (при отсутствии затенения) и О (при затенении). Из графика на рис. 6.1 следует, что до значения ** = 25° (высота ряда равна половине расстояния между рядами) для любых углов наклона коллектора значение фактора незатеняемости не

Опускается ниже 0,95. Для углов fi, лежащих в интервале F ±15°, это значение сохраняется в указанных пределах вплоть до т>= 35°. Для систем, работающих в летнее время, фактор затеняемости характеризу­ется более пологим характером кривых с большим горизонтальным участком.

Для рассеянной радиации фактор незатеняемости вычисляют из выражения

*Ьнезю—(1-cosj> )/[2(1 + cosр )].

Произведение факторов заполнения и незатеняемости (рис. 6. Позволяет определить эффективно работающую площадь коллекторе - Аэф в зависимости от их расположения и площади поверхност размещения F;

•^эф заг/заг