СТРУКТУРА И СВОЙСТВА ГАЗОНАПОЛНЕННЫХ ПОЛИМЕРОВ
РАСЧЁТ ДИАГРАММ СЖАТИЯ ЭЛАСТИЧНЫХ ПЕНОПЛАСТОВ С РАЗЛИЧНОЙ ОСТАТОЧНОЙ ДЕФОРМАЦИЕЙ
Особенностью макроструктуры эластичных пенопластов является возможность остаточного искривления тяжей ячеек, что имеет принципиальное значение при оценке их структурно-механических свойств.
Длительное применение эластичных пенопластов в нагруженном состоянии (при хранении и транспортировке в сжатом состоянии, при применении в качестве сидений в мебельной и автомобильной промышленности и т. д.) сопровождается изменением физико-механических свойств пеноматериала, характеризуемым уменьшением его жесткости, возникновением остаточной деформации, изменением вида деформационных кривых. Возникающее при этом изменение ячеистой структуры должно оказать специфическое влияние на механические свойства эластичных пенопластов, поскольку параметры макроструктуры оказывают определяющее влияние на характер деформации пористых полимерных материалов. Поэтому нами исследована связь деформативных свойств эластш - ных пенопластов с изменением макроструктуры при длительном пребывании их в нагруженном состоянии /195/.
Ниже представлены результаты расчёта на основе предложенной нами модели ячейки зависимости свойств эластичных пенопластов от параметров ячеистой структуры при испытаниях в условиях сжатия, поскольку сжимающие нагрузки наиболее характерны для условий эксплуатации этих материалов. Для простоты расчёта рассмотрим поведение изотропного пенопласта с первоначальным отношением продольных размеров ячеек к поперечным, равным единице. Модель использованной для расчёта ячейки аналогична представленной на рис. Ч,2 и отличается лишь искривлением тяжей в исходном состоянии /195/. Ячеистую структуру этого типа образуют тяжи (отержни), соединённые в квадраты. Все со&едние квадраты соединяются друг с другом по углам только во взаимно перпендикулярных плоскостях. При сжатии имеет место кооперативный, энергетически наиболее выгодный изгиб тяжей, что эквивалентно работе тяжей по схеме с одним защемлённым концом.
Непосредственные наблюдения показали, что изменение ячеистой структуры заключается главным образом в изгибе силовых элементов макроструктуры (силовых тяжей) и сохранении их в изогнутом состоянии. Считаем, что начальная кривизна тяжа I/P постоянна по его длине. Тогда с помощью метода упругих параметров /222-223/ были оценены большие перемещения тяжей и, соответственно, уравнение
TOC o "1-3" h z диаграммы сжатия пенополимера /195/: сжимающая ячейку сила вычисляется по формуле о
4р • Е •! Су*
Ряч. . (4.9)
О
Где: р = Jr™P/Ej - параметр силы; Т / 12 - момент инер
Ции сечения тяжа; о ~ начальная длина тяжа;
А степень сжатия образца 8'по отношению к исходной высоте (до испытания его под нагрузкой) на начальном участке диаграммы составляет л
, ( О ) + Ч,
£ = 7; (4Л0)
где: £ - Snnv +8 ~ введенное обозначение;
О 01
£ост относительная остаточная деформация образца;
£ - относительная деформация образца при сжатии;
^и ^ - координаты конечной точки искривлённого тяжа,
Связанные с параметром силы р выражением 8 Гт 2 2 7
= Е(^ ) - -2- + I; = ---(I - Sin1*);
О m p mZ о. /яр. 4
Tn - модуль эллиптического интеграла;
- табличная амплитуда эллиптического интеграла. Поскольку поперечные размеры открытопористого образца после испытания под нагрузкой практически не меняются, эффективное сечение исходной и видоизменённой ячейки останется одним и тем же:
Тогда, используя (4.9) и (4.II) можно определить напряжение сжа-
Тия: о и С77
6 = J&S J^SSUUh - ; (4.12)
24 ( I + fi/Z )2
Ch
Где: J> ~ / в - постоянная отношения толщины тяжа к его длине. При этом, исходя из геометрических рассмотрений, легко получить для исходного образца соотношение для определения J$ :
1 3 ^ f f С 2 + J5 )2 Таким образом, уравнения 4.9 - 4.12 позволили записать в параметрическом виде формулу диаграмм сжатия эластичных открытопорис - тых пенопластов после испытания их под нагрузкой.
Используемая в расчётах (4.10) кривизна тяжей видоизменённых
Образцов связана с остаточной деформацией выражением:
Т А 2. sin2 fr/g £ . ______________________ .
I ♦ Я/г
Где: 1/£ - начальная кривизна тяжей;
- - введённое обозначение.
Можно ожидать, что после однотипного изгиба перекрещивающихся
Тяжей до взаимного их соприкосновения, то-есть при
Fi
( I + fi/4
Наступит процесс смятия тяжей. В этом случае можно оценить увели
Чение напряжения сжатия на няня конечном участке диаграммы:
|
= (Л)Е f+f - I + ^сж р / 4>ст Л J / (I + / "4 |
^ г Т , С т fi
(I + -)CosiL 4
Где: кажущаяся плотность исходного пенопласта (до испытания под нагрузкой); р~ плотность полимера-основы.
Диаграмма сжатия исходного образца расчитывается по более простой формуле (4.3). В случае испытания закрытопористых пенопластов может быть введена поправка на упругое действие газа в замкнутых ячейках, как это сделано, например, в /160/.
Таким образом, выполненные расчёты показывают, как влияет ячеистая структура на изменение характера деформации эластичных пенопластов при предварительном испытании их под нагрузкой.
- 179 -
Были экспериментально оценены свойства эластичных пенопластов в условиях сжатия. Испытания в нагруженном состоянии заключались в сжатии образцов эластичного ППУ на основе сложных полиэфиров (ППУ - - Э-35-0,8) размерами 50 х50 хЗО мм до 70$ от их первоначальной высоты (30 мм) и выдержке материала в течение различных периодов времени при Ю0°С. Параллельно оценивались механические свойства ППУ-Э-35-0,8 на 3-х образцах, причём отклонение отдельных значений контролируемых характеристик от среднего не превышало 8$, В результате испытаний было обнаружено, что поперечные размеры образцов меняются не более чем на 2% при значениях остаточной деформации 0... 60/ош С увеличением длительности испытаний £ возрастает. Однако, после продолжительного "отдыха" в свободном состоянии при той же температуре 100°С образцы в значительной мере восстанавливали свои первоначальные размеры. Следовательно, развитие релаксационных процессов в полимере-основе является причиной изменения ячеистой структуры ППУ-Э-35-0,8, а это, как показывают расчёты, должно привести к специфическому изменению механических характеристик материала.
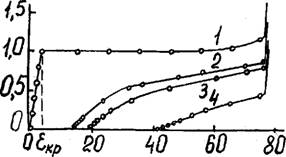
На рис. 4.6 представлены характерные для эластичных ППУ диаграммы сжатия образцов с различной остаточной деформацией. Диаграммы были получены на испытательной машине ZM-20 при скорости деформации образцов 30 мм/мин. Экспериментальные данные позволяют интерпретировать характер диаграмм сжатия ППУ, представленных на рис. 4.6, следующим образом: крутой начальный участок, соответствующий росту нагрузки, отражает прогиб тяжей, когда потеря устойчивости их ещё не достигнута; второй участок, соответствующий возникновению плато на диаграмме или незначительному росту нагрузки при больших деформациях образца (до 60$), отражает изгиб тяжей после потери ими устойчивости; 3-й участок, соответствующий дальнейшему значительному росту нагрузки, отражает сжатие ППУ, уплотнённого до взаимного соприкосновения перекрещивающихся тяжей.
|
CM* |
|
Рис. 4.6. Диаграммы сжатия ППУ-Э ( f - кг/м3), полученные |
|
To t% |
Экспериментально: I - исходный образец; 2 - = 20$; 3 -60$,
U vi
|
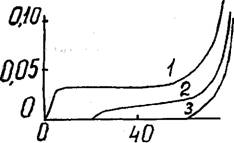
Рис. 4.7. Диаграммы сжатия ГШУ-З ( /~= 46 кг/м3), полученные расчётным путём: I - исходный образец; 2 - £ост = 15$; з. £ост- 20?; 4 - £от = Ш. |
Оказалось, что деформационные кривые исходных образцов, полу^- ченные при их циклическом сжатии и разгрузке, сильно видоизменяются после 1-го цикла. В дальнейшем значительных изменений деформационных кривых не наблюдается (при снятии петель гистерезиса через интервалы времени 20с). Поэтому на рис. 4.6 представлены диаграммы сжатия образцов, полученные при снятии 3-й петли гистерезиса. Очевидно, изменение кривой деформации 2-го цикла связано с развитием релаксационных процессов в полимере-основе, так как после длительного отдыха образцов первоначальная жесткость материала практически полностью восстанавливается.
Из рис. 4.6 видно, что изменение свойств ППУ после длительного сжатия характеризуется увеличением остаточной деформации, причём
Одновременно уменьшаются условный предел прочности ( &' ) и модуль
Кр
Упругости при сжатии, а критическая деформация £Кр увеличивается.
Второй участок диаграммы (плато) сокращается на величину £оот» В
То время как у исходного образца при значительных закритических
Деформациях (£ > £ ) напряжение на диаграмме сжатия сохраняется
Кр
Постоянным, после испытания под нагрузкой напряжение на диаграмме сжатия растёт при закритических деформациях, хотя и значительно меньше, чем на начальном участке диаграммы. Последний участок диаграммы сжатия, соответствующий смятию тяжей, не меняет своего положения. При значениях £ ^ 60% первые два участка диаграммы вы-
О С!
Рождаются совсем.
Было сделано сопоставление данных, полученных расчётным и опытным путёа. Расчётные диаграммы сжатия тех же образцов ППУ представлены на рис. 4.7, Из рис. 4.6 и 4.7 видно, что качественно характф изменения свойств ППУ оказался в обоих случаях одинаковым, что подтверждает определяющее влияние изменения параметров ячеистой структуры на характер деформации пенополимеров. Количественная оценка изменения условной прочности пенопласта в зависимости от величины остаточной деформации (рис.4.8) показывает довольно близкое соот-
|
|
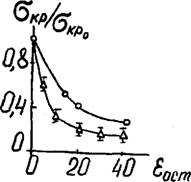
Рис, 4,8. Зависимость услозного предела прочности при сжатии ППУ-Э ( 46 кг/м3) от величины остаточной деформации. Обозначения: О - расчёт; А - эксперимент.
|
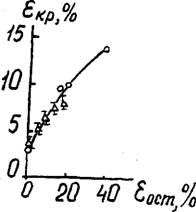
Рис. 4.9. Зависимость деформации при условном пределе прочности ППУ-Э С 46 кг/м3) в случае сжатия от величины остаточной деформации. |
Обозначения: О - расчёт; А - эксперимент.
- 183 -
Ветствие результатов, полученных расчётным и опытным путём. Несколько более резкое уменьшение критического напряжения сжатия (5^ с ростом остаточной деформации при снятии зависимости экспериментальным путём обусловлено, вероятно, дополнительным наложением релаксационных процессов в полимере-основе, что снизило несколько его жесткость. Подтверждением этого является более близкое соответствие расчётных и опытных данных при оценке <5*Кр (рис.9), поскольку расчёты показывают, что эта характеристика определяется лишь параметрами ячеистой структуры и не зависит от свойств полимера-основы. Наконец, расчёты предсказывают (рис.4.7) и эксперимент подтверждает (рис. 4.6), что положение конечного участка диаграммы сжатия, соответствующего смятию тяжей, остаётся без изменения.
Таким образом, представленные в настоящем разделе данные позволяют при оценке деформативных свойств эластичных пенопластов определить, в какой мере изменение параметров ячеистой структуры за счёт остаточной деформации влияет на зависимость (3"= ;/"(£) в условиях одноосного сжатия.