Железобетон

ВИСЯЧИЕ ПОКРЫТИЯ

Висячими покрытиями можно перекрывать помеще­ния особенно больших размеров (стадионы, спортзалы, выставочные павильоны, рынки, кинотеатры, крупные производственные здания). Образуются они из системы вант (гибких тросов), удерживаемых на жесткой опор* ной конструкции (кольцах, рамах, арках), и кровельного; ограждения из сборных плит (железобетонных с приме| нением легкого бетона, армоцементных многослойны^

ИЛИ ИНЫХ плит). 2

Различают висячие покрытия с одиночной системой вант, имеющие поверхности однозначной или разнознач* ной кривизны (рис. XIV.35—XIV.37), и с двойной систе^ мой вант (рис. XIV.38). Висячими покрытиями можно пе* рекрывать помещение любого очертания в плане (прямо­угольные, круглые, овальные, многоугольные и иные).

На рнс. XIV.35—XIV.37 приведены лншь основные разновидности висячих покрытий; в практике встречается значительно большее их разнообразие.

Висячие покрытия устраивают достаточно пологим^ их стрела провисания f в центре покрытия составляет обычно "До—V25 долю основного размера плана.

Ванты в висячих покрытиях применяют с радиальный расположением в плане (рис. XIV.35, a; XIV.37, XIV.38), с ортогональным (рис. XIV.35,6, в, г; XIV.37, а, б; XIV.38, а, б), а также полигональной систе­мы (рис. XIV.36).

Fh, ч>>>>>>>>>>?>

Si

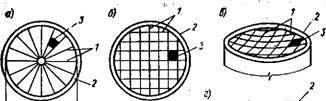
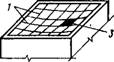
Рис. XIV.35. Схемы висячих покрытий с поверхностями двоякой од­нозначной кривизны, с одиночной системой радиальных и ортогональ­ных вант

И — круглое в плане с радиальным расположением вант; б — то же, t ортогональным расположением вант; в — овальное в плане; г — пря­моугольное в плане; 1 — ванты; 2 — опорное жесткое кольцо (замк­нутая рама); 3— плиты кровельного ограждения

Применяют также висячие покрытия с поверхностью Одинарной кривизны (цилиндрической) с вантами одного направления в плане (рис. XIV.39), закрепляемыми на контурных прямолинейных жестких брусьях. Реакции вант воспринимаются наружными оттяжками или внут­ренними упорами (используемыми в спортивных и других помещениях для зрительных трибун). Покрытия с ванта­ми одного направления могут делаться и безраспорными, если применить двухпоясную систему вант по схеме рис. XIV.38, б.

Монтируют висячие покрытия без лесов и подмостей. В этом их существенное преимущество перед другими 1 пространственными покрытиями.

Г Свободно подвешенная на жестком контуре мембра­на висячего покрытия обладает ничтожной жесткостью „ на изгиб и потому весьма деформативна в поперечном направлении. С изменением вида нагрузки заметно изме­няется ее геометрическая форма, что наблюдается, на­пример, при концентрации снежных отложений или при ветровых отсосах на подветренных частях покрытий с во­гнутыми поверхностями. Чтобы обеспечить стабильность геометрической формы, железобетонные висячие покры­тия необходимо предварительно напрягать.

Покрытия, приведенные на рис. XIV.35, могут подвер­гаться предварительному напряжению двумя способами.

Рис. XIV.36. Схемы висячих покрытий с поверхностями дво­якой однозначной кривизны, с одиночной полигональной Бай­товой системой

— главные (угловые) ваиты;

— вспомогательные ваиты;

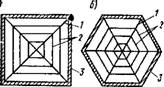
3— контурная рама

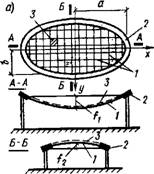
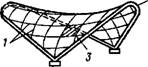
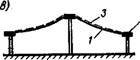
Рис. XIV.37. Схемы висячих покрытий с поверхностями двоякой дву« значной кривизны, с одиночной системой вант, с опиранием

А — по контуру; б—иа два фундамента; в — по контуру и на цент­ральную опору; 1 — ваиты; 2 — опорное кольцо (арка); 3 — илиты кровельного ограждения

Ванты натягивают домкратами после замоиоличи­вания швов плит кровельного ограждения. В этом слу­чае ваиты размещают в каналах, полости которых впо­следствии заполняют раствором.

Ванты натягивают до замоиоличивания швов плит кровельного ограждения с помощью монтажной пригруз - ки, размещаемой на плитах или на подвесках к вантам. После заполнения швов раствором и приобретения им проектной прочности пригрузку снимают. В результате перекрытие приобретает предварительное напряжение.

В обоих способах предварительного напряжения вися­чих покрытий кровельное ограждение играет активную роль.

Покрытия, изображенные на рис. XIV.37, а, б, имеют геометрическую форму, стабильность которой достигает-
^ЙТЬ

V/yy;wyyyy/;yyyyyyyyyyyy?/A

УУУ/УУ-'уууууУУУУУУУУУУУУУ//У/УУУУ/УУУУіУ////)>///у

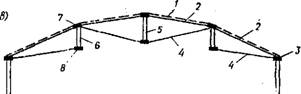
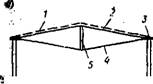
Рис. XIV.38. Схемы висячих покрытий с двойной системой вант

В—с опорным кольцом и одним распорным элементом; б— то же, в несколькими распорными элементами; в — многокольцевое с цент­ральным распорным элементом н осеснмметричным ридом распорных элементов; 1 — плнты кровельного ограждения; 2 — напрягающие ванты; 3 —опорное жесткое кольцо (замкнутая рама); 4 — несущие ванты; ,5 — распорный барабан; 6 — стоечные распорки; 7—проме­жуточное кольцо верхнее; 8 — то же, нижнее

Ся натяжением поперечных вант, уложенных на продоль­ные свободно подвешенные на контуре ванты.

В висячих покрытиях с двойной системой вант (рис. XIV.38) Нижняя несущая система приобретает предвари­тельное напряжение при натяжении верхней напрягаю­щей системы вант.

При этих способах предварительного напряжения оно осуществляется проще, но на устройство вант расходует­ся больше стали. Кровельное ограждение в этих системах играет менее активную роль.

Висячие покрытия имеют хорошие технико-экономй - ческие показатели, близкие лучшим показателям других видов пространственных тонкостенных покрытий.

При расчете висячих покрытий полагают, что вся на­грузка покрытия воспринимается одними вантами; кро­вельное ограждение может работать только на сжатие; ванты могут работать только на растяжение, они совер­шенно гибки (без поперечной жесткости на изгиб) и не - растяжимы.

Расчет висячих покрытий при нагрузке любого вида в общем случае представляет сложную задачу. Однако для отдельных симметричных конструкций при некото­рых видах нагрузок вчзможны простые решения.

Расчет покрытий с радиальным расположением вант. Покрытие, круглое в плане, с расстоянием между ванта­ми b (по периметру покрытия), нагружено равномерно распределенной (по - проекции покрытия) нагрузкой q (рис. XIV.40, а). Каждую нить при такой нагрузке рас­считывают самостоятельно (рис. XIV.40,б).

Учитывая, что опоры ванты находятся на одном уров­не и что реактивное давление направлено по касатель­ной к оси ванты в месте закрепления, вертикальные со­ставляющие опорных реакций ванты в силу симметрии грузовой схемы

A = B = 0,5qbr. (XIV. 63)

Составим уравнение моментов сил на левой половине ванты относительно точки О (рис. XIV.40, б), находим

H = qbrmfe• (XIV.64)

Ванты рассчитывают на усилие

Nb = Va2 + т.

Сжимающее усилие N в кольце (рис. XIV.40, в), на­ходящемся под погонным радиальным давлением Нt =

N = Htr — qr3/6fc (XIV. 65)

Расчет покрытий с ортогональным расположением вант. Пологое покрытие, эллиптическое в плане, загру­жено равномерно распределенной (относительно проек­ции покрытия) нагрузкой (рис. XIV.39).

В висячем покрытии возникает только безмоментное напряженное состояние. Оно описывается уравнением (XIV.1), в котором должно быть принято Nxу=0 (каса­тельные силы ничем не воспринимаются). Принимая во внимание выражения (XIV.2) и (XIV.3), получаем

Nx дЧ! дх + Ny дЧ/дуЪ = —q. (XIV.66)

С помощью этого уравнения решаются два варианта задачи.

Вариант 1. Известны: нагрузка q и натяжение Nx— =Ny (одинаковое в обоих направлениях); требуется определить уравнение поверхности.

Гру зоба я площадь

S

6)

Іс. XIV.39. Схема висячего ытия с поверхностью оди - оной кривизны (цилиндриче­ской). с вантами одного на - г правления в плане

Fe-—поперечный разрез здания; Р— план (часть здания); /— КОНтурный прямолинейный же­лезобетонный брус; 2 — ванты; f— кровельные плиты; 4 — ко­лонна; 5 — упор; 6 — оттяжки

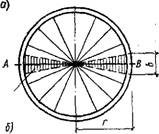
Рис. XIV.40. К расчету висяче­го покрытия, круглого в плане, с радиальным расположением вант

З—план; б—расчетная схема ванты; в — расчетная схема опорного жесткого кольца

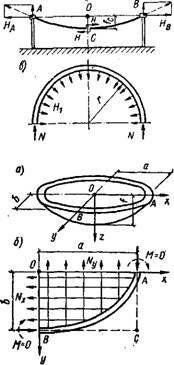
Ряс. XIV.41. К расчету висяче­го покрытия, эллиптического в майе, с ортогональным распо - ; ложением вант

T—геометрическая схема; »— расчетная схема покрытия в плане

Ga-fllHTrn-^— -^-гтттттїїП

г/з т г

Форма поверхности висячего покрытия, эллиптическо - о в плане, загруженного равномерно распределенной на - рузкой, близка к поверхности эллиптического параболо­їда (рис. XIV.41.fl):

! 4 r = t{-(xla)*-(ylb? h (XIV.67)

ІІ' і;

Где а и Ь — известные параметры эллипса в плане; f — искомая стр ла провисания поверхности.

TOC o "1-3" h z Кривизны этой поверхности I

Dhldxl = - 2//а2; д*г/ду* = - 2f/b*. (XIV.6в|

Стрелу провисания можно определить, использовав в уравнении (XIV.66) принятое натяжение и кривизиь! поверхности (XIV.68): ]

F = qa*bV2Nx (а? + (XIV. 69)

Вариант II. Заданы нагрузка и уравнение поверхно-і сти; требуется определить усилия Nx н Ny в покрытии, (рис. XIV.41,б). "

Положим, что покрытие загружено равномерно рас-; пределенной нагрузкой q его поверхность описывается; уравнением (XIV.67). і

Рассматривая четвертую часть покрытия (рис^ XIV.41,6), примем условие, чтобы изгибающий момент в опорном кольце был равен нулю в точках Л и В. Из; уравнения моментов сил, действующих на выделенную часть кольца, взятых относительно точки С, находим

Nxbl = NycP.. (XIV. 70)

Используя это соотношение в уравнении (XIV.66) при кривизнах (XIV.68), находим

Nx = qa2/4f н Ny = qbV4/. (XIV. 71)

Несмотря на различные значения усилий Nx и NyJ нагрузка покрытия q распределяется на ванты обоих на| правлений поровну, а именно с учетом выражений! (XIV.68) и (XIV.71), і

Qx — — Nx дхі = (qa2/4f) (2//а2) = q!2. 1

Аналогично находим, что qv=qj2. j

Нетрудно показать, что при данных условиях опорное? кольцо испытывает центральное сжатие не только в точ| ках А и В, но и по всей длине. «]

Для висячего покрытия в форме гиперболического па«| раболоида (см. рис. XIV.37, а) уравнение и натяжений поверхности следуют зависимостям: |

Г = h (х/а)? - h (y/b)>; (XIV.

Nx = (q + p) a?/2/i; Ny = рЬ*Щг. (XIV.73)1

Здесь ваиты продольного направления воспринимаю^ нагрузку q полиостью и еще «пригрузку» р, образующую юся от натяжения поперечных вант. і

Усилия в вантах гиперболического параболоида боль-?

*, чем в вантах эллиптического параболоида. Опорное Ольцо работает на внецентренное сжатие.

Отметим, что в рассмотренных задачах распор Н по лине вант не меняется, усилие же в них

Ц = + (XIV. 74)

Десь Q — поперечная снла, вычисленная для вант по аналогичной лочной схеме от долн нагрузки, приходящейся на ванты данного Управления.