Ленточные фундаменты под несущими стенами
Под несущими стенами ленточные фундаменты делают преимущественно сборными. Они состоят из блоков - подушек и фундаментных блоков (рис. XI 1.9,а). Блоки - подушки могут быть постоянной и переменной толщины, сплошными, ребристыми, пустотными (рис. XII.9,б). Укладывают их вплотную или с зазорами. Рассчитывают только подушку, выступы которой работают как консоли, загруженные реактивным давлением грунта р (без уче-
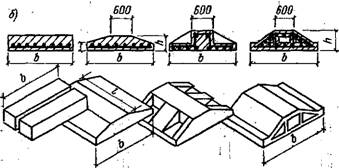
, Рис. XII.9. Сборные ленточные фундаменты под стенами '' о —общий вид; б — типы1 блоков-подушек фундаментов; в —к расчету подушки фундамента; I — фундаментные блоки; 2 — блбкн-по -
Душки
Та массы подушки и грунта на ней). Сечение арматуры подушки подбирают по моменту
Где I — вылет коисоли (рис. XII.9, В, сечеиие 1-І).
Толщину сплошной подушки Л устанавливают по расчету на поперечную силу Q—pl, назначая ее такой, чтобы не требовалось постановки поперечной арматуры.
2. Ленточные фундаменты под рядами колонн
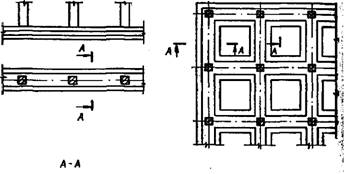
Ленточные фундаменты под рядами колонн возводят в виде отдельных лент продольного или поперечного (относительно рядов колонн) направления (рис. XII. 10, а) И в виде перекрестных лент (рис. XII. 10, б): Ленточные
23—943 353
А)
7777
7777
Вариант поперечного сечения
![]()
Ишдіімит
В)
Ж
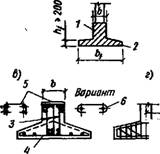
Рис. ХІІ.10. Ленточные монолитные фундаменты под колоннами
А—отдельные ленты; б — перекрестные ленты; в — армирование ленточных фундаментов в поперечном сечеини; г — то же, в продолы ном направлении; 1 — ребро; 2 — полка; 3 — сварные каркасы; 4—• Нижние сварные сетки; 5 — верхние сварные сетки корытообразные; 6 — то же, плоские
Фундаменты могут быть сборными и монолитными. Они имеют тавровое поперечное сечение с полкой понизу. При грунтах высокой связности иногда применяют тавровый профиль с полкой поверху (см. вариант сечения I—I на рис. XII. 10,а, б). При этом уменьшается объем земляных работ и опалубки, но усложняется механизирован* ная выемка грунта.
Выступы полки тавра работают как консоли, защемленные в ребре. Полку назначают такой толщины, чтобы при расчете на поперечную силу в ней не требовалось армирования поперечными стержнями или отгибами. При малых вылетах полка принимается постоянной вы-
Йоты; при больших — переменной с утолщением к ребру. L Отдельная фундаментная лента работает в продольном направлении на изгиб как балка, находящаяся под воздействием сосредоточенных нагрузок от колонн сверху и распределенного реактивного давления грунта f снизу. Ребра армируют подобно многопролетным балкам. (Продольную рабочую арматуру назначают расчетом по формальным сечениям на действие изгибающих моментов; поперечные стержни (хомуты) и;отгибы — расчетом, Іо наклонным сечениям на действие поперечных сил. 'Для повышения жесткости фундаментов их поперечное - Течение подбирают При низких процентах армирования, ^однако не ниже минимально допустимого по нормам для - изгибаемых элементов. При конструировании необходи - . мо предусматривать возможность неравномерного загру - жения фундамента в процессе возведенйя сооружения и неравномерных осадок основания. С этой целью в ребрах устанавливают непрерывную продольную верхнюю и нижнюю арматуру ц=0,2...0,4 % с каждой стороны.
Ленты армируют сварными или вязаными каркасами (рис. XII.10,в, г). Плоских сварных каркасов в поперечном сечении ребра должно быть не менее двух при. ширине ребра 6=^400 мм, не менее трех при b = 400...800 мм и не менее четырех при Ь>800 мм. Верхние продольные стержни сварных каркасов рекомендуется укреплять на всем протяжении в горизонтальном направлении сварными сетками (корытообразными или плоскими с крюками на концах поперечных стержней), а также в продольном направлении с помощью поперечных стержней в каркасах не реже чем через 20D (где D — диаметр продольных стержней).
При армировании ребер вязаными каркасами число вертикальных ветвей хомутов в поперечном сечении должно быть не менее четырех при 6 = 400...800 мм и не менее шести при Ь>800 мм. Хомуты должны быть замкнутыми диаметром не менее 8 мм с шагом не более Ы.
Расстояния между стержнями продольной рабочей арматуры можно назначать по общим правилам; в тяжелых фундаментах для увеличения крупности заполнителя в бетоне эти расстояния следует принимать не менее 100 мм. В расчетное сечение арматуры ленты включают продольные стержни каркасов и сеток. Часть нижних продольных рабочих стержней (до 30%) может распределяться по всей ширине полки.
,23* 355
£
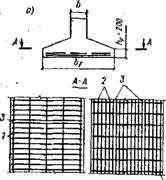
На рис. XII.11 показано армирование полок сварными и вязаными сетками (отдельными стержнями). Целесообразно применять широкие сварные сетки с рабочей арматурой в двух направлениях, используя продольные
Стержни как арматуру лент, а поперечные — как арматуру полки. Узкие сетки при армировании укладывают в два ряда (рис. XII.11,а), размещая в нижнем ряду сетки с рабочей арматурой полки, Сетки укладывают без нахлестки, за исключением верхних, которые в продольном направлении соединяют внахлестку без сварки по правилам соединения сварных сеток в рабочем направлении. При больших вылетах полок (более 750 мм) половина рабочей арматуры может не доводиться до наружного края на расстояние /з=0,5Х'і— —2Ы (рис. ХП.11,б, в). Если в полке возможно появление моментов обратного знака, то предусматривают верхнюю арматуру (см. рис. XII.10, в, пунктир).
3. Расчет леиточных фундаментов
Общие сведения. В зада чу расчета ленточного желе зобетонного фундамента вхо дит: определение давленш грунта по подошве фунда мента из расчета его совме стного деформирования с основанием, вычисление внутренних усилий, действующих в фундаменте, установление размеров поперечного сечения ленты и ее необходимого армирования.
Сетки верхнего ряда
Сетки г. нижнего ряда ' ■ в) 1,>750 6 '' F T
■ Н-4 Крюки только при I ~F~T Гладких стерших 1-І из Стали класса A-I
L,'750
|
И |
Й |
1-1-
Рис. XI 1.11. Армирование ленточных фундаментов
А — узкими стандартными сварными сетками; б — нестандартными сварными сетками; в — Вязаными сетками; 1 — рабочие стержни полки; 2 — тоже, ленты; 3— стыки сварных сеток
Расчет деформаций основания и анализ его результа^
Ов, по требованиям о допустимой величине абсолютной йдкй,' фёДНёй' осадки,1 относительной неравномерности |§Ф&д6к, крена и других показателей, а таюкё устайовле - Шйе' значения расчетного Давления на осйование Rser Производят по указаниям норм проектирования оснований зданий и сооружений.
Ленточный фундамент и его основание работают под Нагрузкой совместно, образуя единую систем|у. Результатом их взаимодействия является давление грунта, развивающееся по подошве. При расчете различают фундаменТы: абсолютно жесткие, перемещения которых Вследствие деформирования конструкции малы по сравнению с Перемещениями основания, и гибкие, деформируемые, перемещения которых соизмеримы с перемещениями основания.
'f К абсолютно жестким могут быть отнесены ленты тбОЛьшого поперечного сечения и сравнительно малой Длины, нагруженные колоннами при небольших расстояниях между ними.
Ленты большой длины, загруженные колоннами, расположенными на значительных расстояниях, относятся к деформируемым фундаментам. . , ( ;
' Простыми математическими зависимортямгі нё представляется возможным выразить физические свойства всего многообразия грунтов и их напластований.
В нормах проектирования оснований зданий и сооружений указывается, что расчетную схему основания (упругое линейно или нелинейно деформируемое полупространство; обжимаемый слой конечной толщины; среда, характеризуемая коэффициентом постели, и т. д.) надлежит принимать, учитывая механические свойства грунтов, характер их напластований и особенности сооружения (размеры и конфигурацию в плане, общую жесткость надфундаментной конструкции и т. п.). При этом рекомендуется выбирать схему либо линейно деформируемого полупространства с условным ограничением глубины сжимаемой толщи, либо линейно деформируемого слоя конечной толщины, если он (на глубийе менее условно ограниченной сжимаемой толщи полупространства) представлен малосжимаемым грунтом с модулем деформации 100 МПа или если размеры подошвы фундамента велики (шириной, диаметром более 10 м), а грунт обладает 10 МПа независимо от глубины залегания малосжимаемого грунта.
В курсе «Основания и фундаменты» [3] отмечается, что метод расчета фундаментов на упруголинейном основании с коэффициентом постели, практикуемый для решения ряда инженерных задач, приемлем при слабых грунтах или при очень малой толще сжимаемого слоя, подстилаемого недеформируемым массивом.
Для ленточных фундаментов, имеющих сравнительно малую ширину подошвы в сравнении с длиной ленты, практическое значение имеет схема основания как упругого полупространства, а при оговоренных выше условиях— схема основания с коэффициентом постели.
Чи
А) И
IV
Г
Г* у
LLUJJJJ. X
I
TOC o "1-3" h z В) , Л, Р,ІГР, І2 Я ■
* Зі 2 / ш; ?♦ З *
), ПЛІТ) п *
/Fj Xj X2 X ^ Xp Xj X^ XT
И
.ЩЩШШЩЦЦ
P ШНШ5
M-4
Www.
Рис. XI 1.12. К расчету ленточного фундамента как балки на упругом полупространстве
А — расчетная схема; б — основная система; в — перемещения оси ленты под действием сил ХІ=І; Г — то же, поверхности основания; д — эпюра давления по подошве леиты; е — эпюра изгибающих моментов в ленте
Расчет ленточного фундамента как балки на упругом полупространстве. Излагаемый ниже метод расчета предложен Б. Н. Жемочкиным и А. П. Синицыным[4]. Непрерывную связь между балкой и основанием в расчетной системе заменяют сосредоточенными абсолютно жесткими стержнями (рис. XII. 12,а). Усилия в стержнях принимают равновеликими равнодействующей давления, равномерно распределенного по площади подошвы, соот-
Ветствующей каждому стержню. Обычно расстояния между стержнями назначают одинаковыми^ а число участков— равным 9—11.
Основную систему можно получить (по смешанному •методу расчета статически неопределимых систем), отделив балку от основания, заменив при этом действие
Стержней действием усилий Х0 и вводя заделку в
Середине балки (рис. XII.12,б). Неизвестными при этом оказываются усилия Х0, ..., и. осадка заделки у0. Значения неизвестных находят из решения системы уравнений
• • 6о<Л + «оЛ + ^02-^2 + • • • + Д0Р + У а = Ви*. + ви*1 + 612*2 + ... + А1Р + г/о = 0;
Коэффициенты при неизвестных усилиях представляют собой перемещения в системе вдоль действующих усиЛий и состоят из двух слагаемых:
Bhi = Vhi+Ykl. (XII. 13)
Прогиб балки Vki (рис. XII.12, в) вычисляют по правилам строительной механики
J1- dx = a2k(a.-ah/3)/2El = c3ah./&EI, (XII. 14)
Где С0Hi = (Ah/C)2 (3At/C — Ah/C).
Осадку основания Yki (рис. XII.12, г) определяют по формуле
Yhi^{l-^)Fki/nE0c, (XII. 15)
Где Е и цо — соответственно модуль деформации и коэффициент Пуассона грунта; Fhi — функция осадки поверхности основания в точке k при воздействии единичных сил Х, = 1. Значения этой функции, вычисленные иа основе решения соответствующей задачи из теории упругости, приведены в табл. XII.2.
Все перемещения в системе уравнений (XII.12) имеют множитель
ПЕ0с/{-$).
Функцию Fki нужно рассматривать как суммарную от действия двух сил Хі и Х{ одновременно и на своих расстояниях от точки k, для которой определяется перемещение. Например, для F32 следует учесть, что одна сила
Таблица XII.2. Значения функции для определения мадкв поверхности основания как упругой полуплоскости
|
Xjc- |
K. |
|||
|
■ |
||||
|
B/c so2J3 |
6/c = 1 |
B/c = 2 |
;6/C = 3 |
|
|
0 |
4,265 |
3,525 |
2,406 |
1,867 |
|
1 |
1,069 |
1,038 |
0,929 |
0,829 |
|
2 |
0,508 |
0,505 |
0,49 |
0,469 |
|
3 |
0,336 |
0,335 |
0,33 |
0,323 |
|
4 |
0,251 |
0,25 |
0,249 |
0,246 |
|
5 |
0,2 |
0,2 |
0,199 |
0,197 |
|
6 |
0,167 |
0,167 |
0,168 |
0,165 |
|
7 |
0,143 |
0,143 |
0,143 |
0,142 |
|
,8 |
0,125 |
0,125 |
0,125 |
0,124 |
|
9 |
Олп |
0,111 |
0,111 |
0,111 |
|
10 |
0,1 |
0,1 |
0,1 |
0,1 |
Примечание, х — расстояние от точки приложения груза до дайной точки; Ь — шурина балкн; с — расстояние между стержиямн.
ХІ^І находится от точки 3 на расстоянии с, а другая ^2 = 1 — на расстоянии 5с; ординаты их линий влияния, взятые из табл. XII.2, должны быть сложены, и, таким образом, при B/C= 1, F32= 1,038+0,2 = 1,238.
Подстановка выражений (XII. 14) и (XII.15) в (XII.13) дает
6М = (FKi + «°w) (1 - с< (хп-16)
Где а = пЕ0 с4/6 £/ (1 — Но) • (XII. 17)
Прогибы балки со учитывают с одной стороны, так как вследствие заделки одна сторона балки на другую не влияет.
При очень жестких балках Е1 имеет большое значение и а приближается к нулю, при гибких Е1 меньше и а = 0,1..1.
Жесткость балки до образования нормальных трещин в бетоне вычисляют по сплошному сечению балки, как EI, после образования трещин, как значение В по формуле (VII.123).
Перемещения от внешних сил Р (нагрузки) определяют по формуле
AKp = - awkpP{1-tf>)/nEoc< (XII-18>
Где Whp = (flft/с)? (3Ale — Ajc).
!©рдйяата эпюр» реакций • і' ■■><••-■<■
' P'I'== Xjcb. (ХІІІЮ)
Зпюра реакций получается ступенчатой, разрывы в №ей должны быть сглажены (рис. XII.12, д). |р: Изгибающие моменты (рис. XII. 12, е) находят как-в ■Ьнсольной балке. Например, для точки 2 М2 = Х42с + ХЗС + 0,5Х2 (с/4);
Щесь от силы Х2 учитывается часть распределенной на - Црузки, расположенной за точкой 2.
Кроме изгибающих моментов вычисляют также по - веречйые силы Q, действующие на ленту. Ц По найденным М и Q конструируют ленточный фундамент, соблюдая общие указания для проектирования железобетонных конструкций.
Если, балка образована из участков различной жест-
Р
Ьсти, то расчетная Система не изменяется (См: рис.
31.12), но в ней прогибы балки v, k вычисляют с учетом Своей жесткости на составляющих участках.
Расчет ленточного фундамента как балки на упруГой основании с коэффициентом постели. Предпосылкой какого расчета является гипотеза о том, что осадка в данной точке основания не зависит от осадки других точек и прямо пропорциональна давлению в этой точке.
Согласно этой предпосылке, основание проседает только в пределах подошвы сооружения. В действительности основание вовлекается. в работу и за пределами фундамента.
Для балки на упругом основании с коэффициентом постели су (рис. XII.13) погонное давление со стороны Грунта в месте, фиксированном расстоянием х, равно:
Q{X)^Bp = BCyYt (XII. 20)
Тде Су — коэффициент постели, ориентировочно равный: при весьма слабых грунтах 0,3—1, при слабых грунтах 1—3, при грунтах средней плотности 3—8 (кг/см3); Ь — ширина подошвы; р — отпор грунта (давление на грунт); у — осадка грунта и балки на расстоянии х от Ее конца (начало координат).
Продифференцируем это выражение дважды:
Q" = Bcyi/'. (XII.21)
Учтем зависимости, известные из сопротивления материалов:
У" = _ (M/Eiy, Q — Pg = М" или Q" = MIV, (XII.22)
Где под ро подразумевается линейная функция нагрузки!
Подставив зависимости (XII.22) в выражениё (XII.21), после несложных преобразований получим дифференциальное уравнение
(XII. 24)
(XII. 23)
0,25s*Mlv + M = 0,
В котором
S^VbEIIbCy
Имеет линейную размерность и называется линейной характеристикой балки на упругом основании. '
При //«<;0,75 (где I — длина балки) балки называ - j ются жесткими (в них деформациями изгиба можно пренебречь); при 0,75<//s<3 — к ор о т к и м и; при L/S>.3 — длинными. Указанные границы условны, поэтому, в практике допустимы некоторые отклонения. Общее решение уравнения (XII.23) имеет вид =
М = Q cos (р + С2 е-ч> sin (р + С3 е9 cos (р + С4 еф sin <р, (XII.25 Ц
Где <F>**X/S, причем х — текущая координата.
Длинные балки. В длинной балке со схемами загру - Шрннй по рис. XII.14 на конце х—1 момент и поперечная Шла имеют нулевые значения, т. е. М = О и
Q = DM/Dx = 0.
Цти условия соблюдаются, если в выражении (XII.25) иринять С3=0 и С4=0.
К Следовательно, общее решение для длинной балки Цш данной схеме загружения
М = Cie_<p cos ф + С2 е-® sin <р. (XII.26)
Отметим как вывод, что параметры одного конца длинной балки на другой конец не влияют.
Последовательное дифференцирование уравнения ІХІІ.26) дает выражения для поперечной силы Q и EI- Цратных перемещений: осадки W=EIy и углы поворота »'=Е1у'. Одновременно с осадкой балки находим давление на грунт с учетом выражений (XII.20) и (XII.24):
Q — Bey У = Bcyw/El = 4ai/s4. (XII.27)
Таким образом,
Q = M' = [— Cj е-41 (cos ф + sin ф) - f C2 e(cos Ф — sin ф)]/«;
(XII. 28)
W =s 0,250s4 = 0.25УИ's4 = 0,5s? (C, e~v sin ф — C2 e~v cos ф);
(XII. 29)
W = 0,5s [СІ e-v (cos ф — sin ф) + C2 e-"1 (cos ф + sin ф)]. (XII.30)
Постоянные интегрирования Q и C2 определяют из граничных условий.
Для схемы I (рис. XII.14, а)—загружение балки сосредоточенной силой Ро на конце (в начале координат) — При х=0, ф=0 имеем Af=0 и Q=—Р0 (положительное направление поперечной силы вверх). Из выражений {XI 1.26) и (XII.28) находим, что Сі=0 и С2 = —sPe, а Потому
М =— SP0 е-ф sin ф; Q =— Р0 е-41 (cos ф — sin ф); (XII.31)
W= (s®/2) Pa е-1" cos ф; W' =— (sa/2) P0 е-1" (cos ф + sin ф) .
(XII. 32)
Для схемы II (рис. XII.14,б) —загружение балки сосредоточенным моментом М0 на конце (в начале координат) — при *=0, ф=0 имеем М=М0 и Q=0. Из выра-
Жений (XI1.26) и (XI 1.28) находим, *то Сі = С2=Ш0 т М =[М0 Ё~? (cos Ф + sin Ф); Q =—(2/s) М„ sin ф; (XII. Зс W == (s2/2) М„ E-v (віп. ф — cosf); ш' = sMn Е"4* соэ ф. (Xll.34
Из этих решений, можно получить коэффициенты вли яния перемещений для загруженного конца балки: прі ІИ0=1 имеем £/-кратные: угол поворота аи и осадку а2 (рис. XII.14,б), а при Q0=f I имеем £У-кратные: осадку А22 и угол поворота Аі2 (рис. XII.14, а) • ■ і
Au = s; а12 = а21 =— s2/2; а22 = s3/2. (XII.35
В схеме III (рис. XII. 15, а) в силу ее симметрии на каждую полубалку действует половинная нагрузка, при< чем сечение под грузом не поворачивается. Следовательно, при х=0, <р=0 имеем Q = ^-P0/2 и W'=0. Из выражений (XII.28) и (XII.30) находим С — —С2— —PQs/2, поэтому
(Р0/4) Se-V (совф-віпф); Q =— (Р0/2) е^соэф; (XII.36]
W = (/>„/4) s3 е^41 (sin ф + cos ф); Ш' =— (Я0/4) s2 е-'1 siri ф.
(XII.37)
В схеме IV (рис. XII.15, б) в сиЛу ее обратной симметрии на каждую полубалку действует половина внешнего момента, причем осадка под моментом равна нулю^ Таким образом, при *=0, <р=0 имеем М=М0/2 и W — =G. Из выражений (XII.26) и (XII.29) находим С1 = Л10/2 и С2 = 0,
Поэтому
Мі = (Лу2) е cos Ф; Q =— (M0/2s) Е~9 (cos ф + sin ф); (XII.38)
W = 0,25s? М0 E~v sin ф; W' = 0,25sAf0 Е"9 (cos ф — sin ф).
(XII. 39)
При загружении длинной балки несколькими нагрузками решение может быть получено суммированием отдельных решений по схемам I—IV.
Короткие балки. В коротких балках (при 0,75< <//s<3) решение (XII.25) приводит к громоздким формулам. Между тем в практике проектирования ленточных фундаментов короткие балки встречаются значительно реже, чем жесткие и длинные. Поэтому ограничимся рассмотрением лишь одной из практически важных задач — балки, загруженной двумя симметрично рас-'
Положенными на ней сосредоточенными грузами (рис. XII.16, а). Приведем результаты-приближенного решения!, произведенного вариационным методом Лагран - жа — Ритца. Уравнения прогибов и углов поворота балки
У = а + а2 (х4 — 1, ЪР X[5]); (XII. 40)
У'=а2( 4х3 — ЗЙх). (XII.41)
В них постоянные параметры
Ах = (2Р/су1) (1 + 0,1125/M/fi); (XII.42)
А2 = (2Р! су I) (А! В),
Где
A = g«-l,5^ + 0,112; (XII.43)
В = 4,8EJ/Cy + 0.009I/4.
Учитывая особенности данного приближенного решения, эпюры М и Q нужно строить не по формулам М — ——Elw" и Q——Elw"' (так как принятая функция W в третьей производной скачка не имеет), а графоаналитическим методом "по эпюре давления грунта Q=Bcyy, где прогибы у определяют по выражению (ХП40).
Эти формулы могут быть использованы для случая загружения балки сосредоточенным грузом 2Р в ее середине (риЬ. XII.16,б), если в них принять 1=0. -
Жесткие балки. Давление на грунт по подошве жестких балок (при i/s<0,75) определяется по формулам сопротивления материалов без учета деформаций самих балок, в предположении, что их жесткость ЈY=do. По краям балки в точках / и 2 (рис. XII.17) напряжение грунта:
От действия момента Мо
= = (XII -44)
От действия СИЛЫ Qo
Zr-QJF±Q*A,W^M (XIL45)
По краям балки осадки грунта
Ум Уш — °ш/сг/;
(XII.47)
УК? =—0,5y2Q= CTjq/Cj,;
Углы поворота
АМ = ЪУш! а = Ъ*ш1асу-
Приняв в выражении (XII.44) М0= I, из первых формул выражений (XII.46) и (XII.47) находим Е1Ь-крат-; ные перемещения края 2 жесткой балки — угловое ац и линейное a2i — с учетом выражения (XII.24):
Ац = 2 (6/а3) ЕІьІЬсу == 3s4/a3; (XII.48)
A2l = ЬЕІьІаЧсу =— 1,5s4/a2. (XII.49)
(XII. 46)
Полагая в выражении (XII.45) Q0 = l. из второй фор-
Ml
О)
Ґ~ р
0,75s
L*3s
Ті
Таї
,у7777777777777^77777777777^КІ!77777>
Є3б
К
Ml
В
Рї
Fir 1.
'Мп
'III lintel 11 ITT
V
![]()
-тг
0'?с< 0,75s
І"
|
"ч |
MQ'MQ * І N |
F {A |
|
|
1 - |
- |
||
|
Е7б п L*3s |
V S |
Qo |
Qo 3 s |
Рис. XI 1.18. К расчету комбинированных схем
А — сочетание жесткой и длинной балки; б — концевой участок ленточного фундамента; в — сопряжение подпорной стенки с полом; Г — узел сопряжения промежуточной колонны с фундаментной балкой; 1 — жесткая балка; 2— длинная балка
Мулы (ХІІ.46) находим Е]ь-Кратное линейное перемещение края 2 балки:
А22 = 8 Eh/obey = S*/a. (XII. 50)
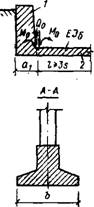
Комбинированные схемы часто встречаются в практике. Они образуются сочетанием жестких и длинных балок (рис. XII.18), Момент М0 и поперечную силу Q0
L
|
Is |
3s |
|||||
|
0.35Р, |
||||||
|
УОЛР, -Ш |
■и4н |
JUMw
,.„ 1 Я 7/р
От
Tlsj^ 7 Р,
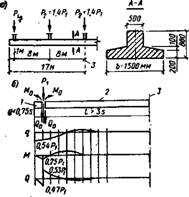
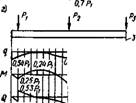
Рис. ХІІ.19. К примеру XII.1
А — расчетная схема; б — эпюры при действии крайнего груза; В — то же, промежуточного груза; г — суммарные эпюры; 1 — Жесткая балка; 2— длинная балка; 3 — середина ленточного фундамента
(XII.51)
В месте их сопряжения определяют из условия отсутствия взаимных перемещений краев балок. Для схемы на рис. XII. 19, а эти условия выражаются уравнениями:
Аи К + «12 Q0 + аїр = 0;
«21 М6 + «22 <Эо + «2Р = 0,
Где 0ц, а12=в2і, «и представляют £/б-кратные взаимные перемещения, получаемые суммированием £7б-кратиых коэффициентов влияния краевых перемещений составляющих балок, а М0. <Эо — неизвестные значения момента и поперечной силы в месте контакта обеих балок.
И (ХІІ.48) —( ХІІ.49),
(XII. 52)
Учитывая формулы (XII.35) находим:
Аи = s + 3s4/a3; а12 = а21 =— s2/2 + 1,5s4/а2; a22 = s3/2 + s4/a.
Грузовые члены представляют £7ь-кратные перемещения от внешних нагрузок р? и а также момента Ми которые возникают в месте приложения искомых М0 и Q0- Учитывая формулы (ХІІ.48), (XII.49) и (XII.27),
AIp —— Ml 3ss/aa;
°2P Mx 1 '5sV - ("I ~ P2) *4/4.
Из решения системы уравнений (XII.51) находим Mo И Qo, которые далее используем для расчета моментов и поперечных сил составляющих балок.
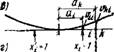
К задачам этого типа относятся: расчет концевого участка фундаментной балки (рис. XII.18, б) и расчет сопряжения подпорной стены, с полом (рис. XII.18,в). Из анализа результатов решения задачи по схеме рис. XII. 18, б, в частности, полученй практически важное заключение о том, что в случае, если лента консольно продолжается за крайние колонну на длину 0,6—0,7s, передача давления на грунт болеіе равномерная. ■
Узел сопрЛжения промежуточной - Колоннії Е фундаментной балкой представляет систему, состоящую из жесткого участка под колонной и двух длинных балок (рис. XII.18,г). В местах примыкания длинных балок к жесткому участку делаем разрезы и в них прикладываем неизвестные усилия Qo и М0. Запишем условие отсутствия поворота конца длинной балки
S/W0 — <?0sa/2 = О (XII. 54)
И условие отсутствия взаимного смещения длинных балок и жесткого участка в местах разрезов
— 0,5s2М0 +0,5s3Q0 — (N — 2Q0) Efb/abcy = 0. (XII.55)
Последний член уравнения представляет EIb-кратную осадку жесткого участка под действием усилия (N —
—2Qo).
Решение уравнений (XII.54) и (XII.55) дает
Q0 N1(2 + a/s); М0 = 0,5Ws/(2 + A/s). (XII.56)
Из формул (XII.56) следует, что чем больше участок А, тем меньше значения Qo и М0.
Пример. Определить давление Q—Bp по подошве и внутренние усилия М и Q, действующие в ленточном железобетонном фундаменте (рнс. XII. 19, а). Линейная характеристика балки, согласно формуле (XII.24), s = 2 м; размеры колонн невелики, жесткие участки фундамента под ними в расчете можно не учитывать.
(XII. 53)
Решение. При действии крайнего груза РГ (рис. XI 1.19,6) имеем сопряжение двух участков: жесткой консоли, в которой а=1 м, г. е. А=0,5s<0,75s, н остальной части балки, в которой L>3S (балка длинная). По формулам (XI 1.52) вычислим £/б-кратные перемещения концов балки в месте разреза при единичных воздействиях М0—1 и Qo=l:
369
Eu = s + 3sVa3 = 2 + 3-24/ls = 50;
24—943
Аг2 = s3/2 + ®*/а=2»/2 + 241 = 20;
A12 =a2i=-0,5s2+ 1,5s4/a2 =—0,5-2г+ l,5-24/1? = 22.
Грузовые перемещения определяем по схеме I (см. рис. XII.14, а), считая Ра—Р в формулах (XI 1.32):
Flip =— 0,№Р1=—2Рц
А2р = 0,5ss = 4PX.
Система уравнений (XI 1.51) принимает вид
50Mn + 22Q0 - 2PX = 0;
22A<0 + 20Q0 + 4P1 = 0.
Решая, находим М0=0,248Я, и Q0=~0,473Яі. Подстановка этих значений в решения по схемам I и II (см. рис. XII. 14) для данного участка балки дает
Q = [0 > 527е—^ cos ф — 0,124E~V (cos ф —sin ф)] Рц М = [— 1,054е~41 sin ф + 0,248 е(eos ф + sin ф)] Я,;
Q = [— 0,527E~V (cos ф — sin ф) — 0,248<Г(|Р sin ф] Pt. По этим выражениям строим эпюры Q, М и Q, принимая значения г — * , sin ф, cos ф для отдельных сечений балки по любому справочнику.
Для жесткого участка балки краевые значения погонных давлений, согласно формулам (XII.44) н (XII.45),
<7i = 6МП/а2 _ 2 Qja = 0,542Яі; q2 6Af0/a2 + 4Q0/fl = 0,404/V
При действии промежуточного груза Я2=1,4Рі (рис. XII.19, в) расчетная схема балкн состоит из двух длинных балок. Используя решение по схеме III (см. рис. XII.15,а), получаем:
Q = 0,35/>i е-<р (cos ф + sin ф);
М = OJPx (cos ф — sin ф); - Q =—0,7Pj cos ф.
По которым строим эпюры Q, М и Q.
Окончательное решение в виде эпюр Q, М и Q находим сумми< рованием отдельных решений от всех грузов на ленточном фундаменте (рис. XII.19, г).
Перекрестные ленточные фундаменты. Приближенный расчет перекрестных ленточных фундаментов выполняют в предположении распределения давления на грунт по закону плоскости для сооружения в целом. Более точный расчет производят как деформируемых балок на упругом основании. Неизвестные усилия взаимодействия лент одного и другого направлений определяют из условия равенства их прогибов в местах пересечения. Крутящие моменты ввиду их малого влияния не учитывают.
Расчет перекрестных ленточных фундаментов как системы балок двух направлений в плане, взаимосвязанных с основанием, рассматриваемым по методу упругого полупространства, весьма трудоемок.
Расчет перекрестных балок на упругом основании с коэффициентом постели значительно проще; в этом случае в дополнение' к изложенному выше возникает задача о расчете узла, состоящего из жесткого подколонника и четырех длинных балок (рис. XII.20). Моменты и усилия в узле определяют по формулам, аналогичным (XII.56); при одинаковой жесткости длинных балок
Qo = Л7(4 + F/Sb); |
Где Г — площадь подошвы подколонника XII.20); Ь— ширина подошвы лент.
4. Взаимодействие сооружений с фундаментами, лежащими на податливом основании
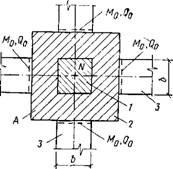
Рис. XI 1.20. К расчету узла сопряжения подколонника и перекрестных лент
1 — колонна; 2 — подколонник; 3 — ленты перекрестного фундамента (длинные балки)
(заштрихована на рис.
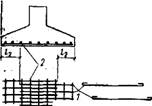
Фундаменты рассчитывают не только из условия совместной работы с податливым основанием, но и с учетом перераспределения нагрузок на основание вследствие собственной жесткости надфундаментной конструкции, если ее жесткость значительна. Например, бункерная эстакада на ленточных фундаментах (рис. ХП.21,а) должна рассчитываться во взаимодействии с уже изученной выше системой, состоящей из фундаментных лент и основания.
371
На значение усилий Рк в колоннах (рис. XII.21,6), являющихся нагрузкой фундамента, значительное влияние оказывает жесткость (EI) с надфундаментной конструкции сооружения. Напряженное состояние бункерной эстакады и фундаментов существенно зависит от изме-
24*
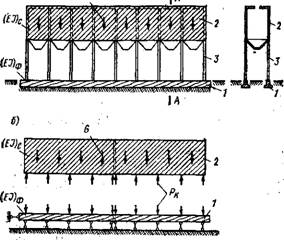
Рис. ХІІ.2). К расчету усилий взаимодействия сооружения с ленточными фундаментами на примере бункерной эстакады
А — общий вид; б — расчетная схема; 1 — фундаментная леита; 2 ^-бункер; 3— колонна
Нения расположения временной нагрузки G (заполнение ячеек) на сооружении.
Как правило, при учете взаимодействия сооружения с фундаментами достигается большая экономия строительных материалов.