ВЛИЯНИЕ ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ И ФИЗИЧЕСКИХ СВОЙСТВ РАБОЧЕЙ ЖИДКОСТИ НА ХАРАКТЕРИСТИКИ НАСОСОВ
Относительный эксцентриситет е = е/г2 оказывает значительное влияние на характеристики насоса. При уменьшении относительного эксцентриситета (е < 0,153 для случая, рассматриваемого на рис. 122) удельная мощность увеличивается за счет уменьшения быстроты действия, так как возрастает погружение а лопаток в кольцо в сечении II—II (см. рис. 109). При этом необходимо отметить, что при уменьшении относительного эксцентриситета уменьшается и эффективная мощность, так как при снижении быстроты действия уменьшается мощность Nсж, затрачиваемая на сжатие. Но так как гидродинамические потери при уменьшении е остаются практически без изменения, эффективная мощность уменьшается значительно медленнее, чем снижается быстрота действия, что приводит к увеличению удельной мощности.
При увеличении относительного эксцентриситета (е >0,153) удельная мощность растет также за счет уменьшения быстроты действия. Однако в этом случае быстрота действия уменьшается вследствие выхода лопаток рабочего колеса из жидкостного кольца. При очень больших относительных эксцентриситетах быстрота действия насоса может стать равной нулю, так как окно нагнетания соединится с окном всасывания, если при угле фсж—фх ни одна из лопаток не войдет в кольцо. Мощность Nсж сжатия при этом также уменьшается в результате уменьшения быстроты действия, однако мощность, затрачиваемая на перемещение жидкостного кольца, увеличивается вследствие затрат мощности на удар при входе лопаток в кольцо. В результате этого возрастает удельная мощность.
Из приведенного анализа следует, что должно быть оптимальное значение относительного эксцентриситета, при котором удельная мощность будет минимальной. Это будет тогда, когда глубина а погружения лопаток в жидкостное кольцо и отход D жидкостного кольца от ступицы равны нулю. Однако при проектировании насоса стремятся обеспечить гарантированное погружение лопаток в кольцо:
А = (0,01 - г - 0,015) г2.
В предварительных расчетах относительный эксцентриситет задают в пределах 0,145 ... 0,125, а затем е рассчитывают из условия соблюдения гарантированной глубины погружения лопаток в жидкостное кольцо.
Относительный зазор б = Д/г2 выбирают на основе экспериментальных данных в пределах 0,011 ... 0,03. При уменьшении относительного зазора возрастают гидравлические потери в зазоре между корпусом и ротором. Увеличение относительного зазора при неизменном относительном эксцентриситете может привести к выходу лопаток из жидкостного кольца (см. формулу 4.4) и, как следствие, к уменьшению быстроты действия насоса.
|
Ща, кВт!(м3/с)
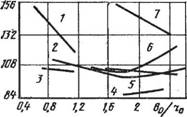
Рис. 123. Зависимость удельной мощности от относительной длины колеса для насоса с различными диаметрами рабочих колес машин: 1 — фирмы «Сименс» (ФРГ), D = 141 мм; 2 — То же, D = 222 мм; 3 — то же, D = 218 мм; 4 — то же, D = 452 мм; 5 — то же, D ■ '!'/ мм; 6 — фирмы «Брюрихардт» (Швейцария), D = 340 мм; 7 — то же, D = 460 мм |
Относительный радиус ступицы колеса v = rjr2 принимают в пределах 0,4 ... 0,55. При v 0,5 увеличиваются размеры насоса, а при v < 0,4 возникает трудность размещения вала необходимого диаметра в ступице колеса.
F-Относительная длина 'колеса Ь0/гй. ' На рис. 123 показана экспериментальная зависимость удельной мощности от относительной длины колеса для машин фирм «Сименс» (ФРГ) и «Бюркхардт» (Швейцария), имеющих различные диаметры рабочих колес. Как следует из рисунка, относительную длину колеса bjr2 следует выбирать в пределах 1,5 ... 2,2. г При движении жидкости в безлопаточном пространстве ее скорость уменьшается при приближении к торцовым крышкам. Это приводит к тому, что жидкостное кольцо дальше отходит от ступицы^в центре колеса и ближегвсего подходит к ступице у торцов. При такой форме внутренней поверхности жидкостного кольца, в, колесах"с'наклонной ступицей (рис. 124, а) в объеме рабочейГячейки," расположенной в сечении I—I (см. рис. 109), остается^меньше газа, а следовательно, увеличивается быстрота
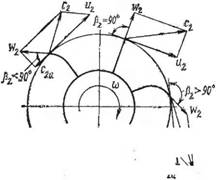
Рис. 125. Абсолютная скорость с2 Жидкости при различных углах наклона лопаток, рабочего колеса
Действия насоса по сравнению с насосом, рабочее колесо которого имеет цилиндрическую ступицу (рис. 124, б). Как показывают экспериментальные работы, * i М 1 оптимальный угол наклона
Иг\ ступицы а = 7 ... 10°. С ид с Передача энергии в насо-
|
|
|
А — быстроты действия иасоса с рабочими колесами, имеющими различные лопатки; б — КПД; 1 — прямые, наклонные вперед; 2 — изогнутые по радиусу
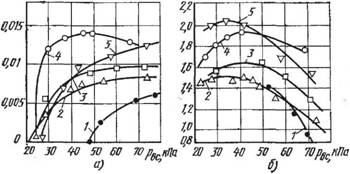
Рис. 127. Зависимости для насоса от давления всасывания при различных углах р2 наклона лопаток рабочего колёса (рабочая жидкость — вода, рн = 98 кПа): А — быстроты действия; б — эффективной мощности; / — 0, = 45°; 2 — = 90°; 3 — 0, = 136°; 4 — Р, = 150°; 5 — Р, = 168° |
|
$мЗ/с |
|
Ие, кВгл |
2 се осуществляется от колеса к рабочей жидкости на стороне всасывания. На стороне сжатия и нагнетания жидкость передает энергию газу, когда сжимает и вытесняет его в нагнетательное окно. При этом скорость жидкости уменьшается. Так как на стороне всасывания происходит передача энергии от колеса
|
ZD П БО во рес нПа 0 Z0 4-0 60 60рвсШ Рис. 126. Зависимости от давления всасывания: |
К жидкости, то лопатки колеса должны быть загнуты вперед (рис. 125), так как в этом случае получает максимальную абсолютную скорость с2 жидкость на выходе с лопаток колеса. Минимальная абсолютная скорость с2 будет при загнутых назад лопатках.
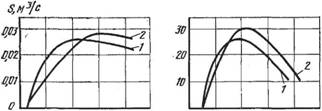
Вперед загнутые лопатки выполняют прямыми и плавно изогнутыми по радиусу. Как показывают экспериментальные исследования, эти насосы с плавно изогнутыми по радиусу лопатками (рис. 126, кривые 2) при прочих равных условиях в области рабочих давлений имеют большую быстроту действия и больший изотермический КПД, чем насосы
С рабочими колесами, имеющими наклонные вперед прямые лопатки (рис. 126, кривые 1).
При увеличении выходного угла наклона лопаток производительность насоса увеличивается (рис. 127, а), но растет и эффективная мощность на валу (рис. 127, б) в результате увеличения мощности на преодоление сил трения в безлопаточном пространстве жидкостного кольца и мощности сжатия газа. Удельная мощность получается минимальной при выходных углах наклона лопаток 150° (рис. 128).
В лопаточном пространстве кольца жидкость совершает сложное движение. При выходе с лопатки колеса она движется в переносном движении со скоростью щ (см. рис. 109) и в относительном со скоростью W2, абсолютная скорость жидкости на выходе с лопатки рабочего колеса с2. Траектории движения жидкости в безлопаточном пространстве В в первом приближении можно принять эквидистантными радиусу корпуса. Тогда в точке А кольца жидкость должна иметь скорость v2, направленную по касательной к траектории своего движения В в безлопаточном пространстве. Разность скоростей
|
С2 и v2 определяет рость wr. |
Ско- WF- "Д
Рис. 130. Зависимости для насоса (р = 26,6 кПа, рн = = 98 кПа) от окружной скорости «г Для различных рабочих жидкостей: А — быстроты действия; б — эффективной мощности; О — вода; О — дибутилфталат; д — масло ВМ-4
Наличие радиальной скорости Wr вызывает образование вихрей при выходе жидкости с лопаток в безлопаточное пространство, что увеличивает затраты мощности на перемещение жидкостного кольца. Наименьшая скорость wr на стороне всасывания (0° ^ <6 < 180°) будет в интервале углов 02 = 135 ... 150° (рис. 129), что объясняет наличие минимума удельной мощности.
Окружная скорость на периферии рабочего колеса и2 — 2Лг2п, М/с, ограничена устойчивостью жидкостного кольца, а также возникновением кавитационных явлений. Устойчивое жидкостное кольцо получают при скорости
(4.13)
«2 = V Зрн/Рш — 2р/рж/ф,
Где ф — коэффициент, учитывающий форму и число лопаток, <р = {[1 — (1 — — V)/(N Tg Р2)] цг}°'в; здесь цг = {1 — л Cos Ра/[2г (1 —V)]}"1.
|
S,M3/C |
|
Ne, кВт |
|
0.15 |
|
U г, м/с |
|
Е/ |
Теоретическая быстрота действия насоса возрастает прямо пропорционально увеличению скорости и2. Однако действительная быстрота действия S растет медленнее, чем скорость и2 (рис. 130, а), что объясняется зависимостью формы внутренней поверхности жидкостного кольца и относительных перетеканий от скорости и2.
|
Н1/д, кВт/(м}/с1 |
|
Z16 Too М юв |
|
П 14 16 Юиг, м/с 6У |
Рис. 131. Зависимость удельной мощности насоса от окружной скорости и2:
О — для различных давлений на всасывании; б — для рабочих жидкостей (р = 26,6 кПа, Рн = 98 кПа) с различной вязкостью; 1 — р = 80 кПа; 2 — р = 60 кПа; 3 — р = 50 кПа; 4 — р = 30 кПа; 5 — р = 20 кПа; 6 — р = 10 кПа; 7 — вода; 8 — дибутилфталат;
9 — масло ВМ-4
Рис. 132. Зависимость Рис. 133. Зависимость коэффициента KT от темпера - КПД насоса от плотности туры Т рабочей жидкости на входе в насос:
Рабочей ЖИДКОСТИ 1 — р — 0,01 МПа; 2 — р = 0,02 МПа; 3 — р = 0,04 МПа
Теоретическая мощность, затрачиваемая на вращение жидкостного кольца, зависит от Til, в то время как мощность сжатия прямо пропорциональна скорости и2. Экспериментально полученная зависимость эффективной мощности от скорости и2 представлена на рис. 130, б. Зависимость удельной мощности от скорости и2 Имеет минимум. Значения оптимальной скорости и2 (скорости ы2. при которой удельная мощность минимальна) зависят от режима работы насоса и вязкости рабочей жидкости. Зависимость удельной мощности J3BH-12 от скорости и,2 для различных давлений всасывания при использовании в качестве рабочей жидкости воды представлена на рис. 131, а. Оптимальные значения окружной скорости лежат в интервале 12 ... 16 м/с, при этом меньшие значения скоростей относятся к большим значениям давлений всасывания. При увеличении вязкости рабочей жидкости оптимальное значение скорости увеличивается. Так, для режима Т = Pjp = 3,7 оптимальное значение скорости увеличивается от 13,5 м/с при работе на жидкости вязкостью 1 • 10"3 Па-с до 15,5 м/с при работе на жидкости вязкостью 80-Ю-3 Па-с (рис. 131, б).
Плотность и вязкость жидкости значительно влияют на характеристики насоса.
Мощность, затрачиваемая на вращение жидкостного кольца, прямо пропорциональна плотности рабочей жидкости, в то время как мощность, затрачиваемая на сжатие газа, не зависит от плотности жидкости. Быстрота действия насоса возрастает пропорционально плотности рабочей жидкости. Рост быстроты действия опережает увеличение мощности, что приводит к незначительному увеличению КПД насоса (рис. 132).
Применение рабочих жидкостей с вязкостью большей, чем вязкость воды, приводит к уменьшению быстроты действия вследствие уменьшения коэффициента /г2 (см. рис. 130, а), увеличению мощности, затрачиваемой на вращение кольца, а следовательно, и эффективной мощности (см. рис. 130, б), в результате чего резко возрастает удельная мощность (см. рис. 131, б) насоса.
Для снижения влияния вязкости на удельную мощность насоса необходимо: выходные углы f>2 лопаток колеса уменьшать от 150° при использовании в качестве рабочей жидкости воды до 135° при использовании в качестве рабочей жидкости масла (вязкостью 37,8-Ю-3 Па-с); относительный эксцентриситет принимать таким, чтобы глубина погружения лопаток в жидкостное кольцо не превышала 2 ... 7 мм; окружную скорость и2 на периферии рабочего колеса увеличивать с 12 ... 14 м/с на воде до 15 ... 20 м/с на рабочих жидкостях вязкостью 80-Ю-3 Па-с.
Температура рабочей жидкости на входе Тт. вх (К) значительно влияет на быстроту действия насоса, поэтому ее следует приводить к быстроте действия S28s (м3/с) при температуре воды 288 К (15 °С):
■$288 = "S/^t. где /гт — коэффициент, определяемый по графику в зависимости от температуры Тт. ЕХ воды и давления всасывания (рис. 133).
4.6 ДВУХСТУПЕНЧАТЫЕ НАСОСЫ
Двухступенчатые насосы применяют в интервале давлений всасывания 15,5 ... 2,5 кПа [2]. При создании двухступенчатых насосов важно правильно выбрать промежуточное давление и окружные скорости на периферии колес первой и второй ступеней. Оптимальное промежуточное давление выбирают, минимизируя удельную мощность или удельную массу насоса. И та, и другая задача для насоса решаются экспериментально-аналитическим путем. При этом делают допущение, что потери в межступенчатых коммуникациях отсутствуют, т. е. рн1 = рц, где рн1 — давление нагнетания первой ступени, Па; ргг— давление всасывания во вторую ступень, Па.
При минимизации удельной мощности
Муд. Ш1п = ш1п/"S |
Где Л'уд — удельная мощность двухступенчатого насоса, кВт/м3; Ne и NeI— Эффективные мощности соответственно первой и второй ступеней насоса, кВт; S — быстрота действия двухступенчатого насоса, м3/с.
Зависимость между отношением давлений в первой ступени и отношением давлений в двухступенчатом насосе аппроксимируется зависимостью (рис. 134)
Тх = 4,19 0,07туст,
ТО
|
|
|
Рис. 134. Зависимость тх От хуст: Д — масло BM-4; О — в°Да |
|
5 П 15 20. Z5 30 35 <Ю 45 50 vgCT |
|
0 — 13,03/13,03 = 1; П — 14,77/13,03 = 1,23; Д — 16,5/13,03 = 1,27; V — 19,07/13,03 = 1,47 Где туст=р„ ц/Pi (рн II—давление нагнетания двухступенчатого насоса, Па; Pi—давление всасывания в первую ступень, Па). |
Доверительный интервал I = ±3,3 при доверительной вероятности а = 0,9. Данная зависимость получена для насосов, работающих на воде при отношении давлений туст = 5 ... 16,2 и на масле ВМ-4 при отношении давлений туст = 5 ... 50,7 [2].
При минимизации удельной массы насоса
Туд. Mln : ITl/S, где т — масса двухступенчатого насоса, кг.
Отношение давлений в первой ступени рекомендуется выбирать в пределах тх = 2...3,5 [1].
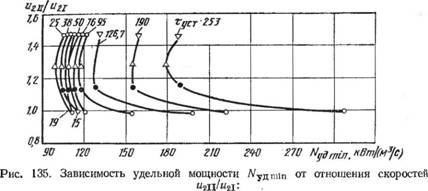
При проектировании двухступенчатых насосов окружную скорость на периферии рабочего колеса первой ступени н21 (м/с) следует выбирать минимальной, исходя из условия получения устойчивого жидкостного кольца [уравнение (4.13)1, а оптимальное отношение скоростей w2ii/w2i = 1.15 ... 1,35 (и2ц— окружная скорость на периферии рабочего колеса второй ступени, м/с) (рис. 135) [2].