ТЕРМОДИНАМИЧЕСКИЕ ОСНОВЫ РАБОЧЕГО ПРОЦЕССА И ОПРЕДЕЛЕНИЕ ОСНОВНЫХ КОНСТРУКТИВНЫХ СООТНОШЕНИЙ
Теоретическая быстрота действия. В насос газ поступает из всасывающего патрубка отдельными порциями, поэтому быстроту действия насоса можно рассматривать как суммарный объем газа, откачиваемый отдельными ячейками в единицу времени. Под теоретической быстротой действия понимают (м®/с)
Sr = ZFhLn
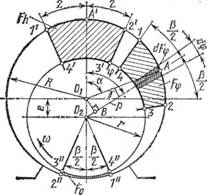
Где Z — число пластин; F^ — максимальная площадь ячейки при угле поворота ротора ф = 0 (рис. 24); L — длина ротора, м; п — частота вращения ротора, с-1.
Максимальная площадь ячейки, образованной радиальными пластинами, (м2)
О
|
2 » -0,50 |
Где р — текущий радиус-вектор, р = = 02Л; г — радиус ротора, м; Р — угол между двумя радиальными пластинами, рад.
Текущий радиус-вектор, т. е расстояние от оси вращения ротора до цилиндра, (м)
При ф = 0 ршах = R (1 + Я); при ф = 180° pmln = R(I-1),
Где R — радиус корпуса, м; Л— относительный эксцентриситет, К — — E/R; е — эксцентриситет, м.
Следовательно, ячейка, имеющая максимальную площадь (и максимальный объем), будет Рис. 24. Изменение площади попереч - располагаться симметрично от - ного сечения ячейки с радиальными
Носительно ЛИНИИ центров ро - пластинами при повороте ротора на
П г г угол ф
Тора и корпуса. Выразив значение р = р (ф) и подставив его в выражение (2.1), после ряда упрощений и преобразований в результате интегрирования получим
Fh = CeR/Z. (2.2)
Тогда Sr = CeRLn, (2.3)
Где С — коэффициент, учитывающий влияние числа Z пластин и относительного эксцентриситета
С = 7t(2-X) + z(2sin-5- + -|-sin-^-) =
= z(p + 2sln-|- + - f slnP--T")- (2-4)
Значения коэффициента С приведены в табл. 2.1.
При числе пластин Z > 12 коэффициент С 4зх. Тогда
S ж AneRLn, S'r » 4NeRL
|
|
Коэффициент С и, следовательно, теоретическая быстрота действия согласно формуле (2.3) возрастают с увеличением числа
|
Таблица 2.1
|
Пластин. Например, при Я =0,15 насосы с Z = 12 имеют ST примерно на 27 % больше по сравнению с двухпластинчатым при том же эксцентриситете. С увеличением относительного эксцентриситета Я коэффициент С уменьшается незначительно, т. е. геометрическая быстрота действия практически прямо пропорциональна эксцентриситету.
Геометрическая быстрота действия насоса прямо пропорциональна площади торцового сечения ячейки максимальных размеров (м^с):
Sr = FhLn,
Где Fjj — суммарная площадь ячеек за один оборот ротора, м2/об, F^ = FhZ = = CeR.
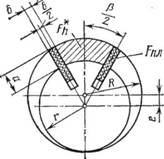
При большом числе пластин (Z 12) суммарная площадь может быть приближенно подсчитана как площадь кольца, очерченного из центра ротора. Внутренний диаметр кольца равен радиусу г ротора, а наружный (R - J- Е). Следовательно, средний радиус кольца равен R, а толщина кольца 2е (рис. 25).
Площадь (м2) и объем (м3) кольца:
FK~Fh = 2nR-2e = 4л eR = 4nXR2 VK = FKL = AneRL = S'r, А максимальная площадь ячейки (м2)
F Fh 4леR ,0
Другой способ нахождения максимальной площади ячейки с радиальными пластинами основан на вычислении алгебраической суммы площадей сегмента, треугольника и сектора (рис. 26):
|
Рис. 26. Максимальная площадь поперечного сечения ячейки при радиальном расположении пластин в пазах ротора при <р = 0 |
|
Рис. 25. Схема для определения Sr насоса при числе пластин 2 > 12 |
Fh — FABC + FaboZ — FDEO2.
Площадь сегмента
РАВС = 0,5R2 (2а' - Sin 2а').
Площадь треугольника FAbO2 = 0,5R2 sin 2а' - f ER sin or'
Площадь сектора
Fi>Eo2 = nrz/Z.
Углы а' и 7 (рад): a' = 0,5(3 + у, у = arcsin (я sin.
Следовательно,
Fh = /?2 [0,5р + V + Л sin (0,5(3 + у) - (1 - Я)2]. (2.6)
Численные значения, полученные по формулам (2.2) и (2.6), одинаковы.
Выражения (2.2) и (2.6) получены без учета толщины пластин. Большое число пластин будет оказывать влияние на уменьшение геометрической быстроты действия насоса вследствие уменьшения площади ячеек, особенно при значительной толщине пластин. Площадь максимальной ячейки с учетом толщины выступающей части пластин (рис. 27) (м2)
Fl^ Fh — Fпл = Fh— 6 a,
Где Fnn — площадь выступающей части пластины, м2; 6 — толщина пластины, м; а—выступающая часть пластины, м,
А = е (1 + cos ~2-------------- sin2 '
При большом числе пластин (Z 12) вылет пластины обычно принимают а я* 2е. В этом случае при Я = 0,18 и Z = 12 ошибка не превышает 2 %. Тогда
F*h = Fh - 2е8. (2.7)
Суммарная геометрическая площадь ячеек насоса за один оборот ротора с учетом толщины пластин
F'h = F'hZ = 4neR - 2ебZ = 2е (2лR - бZ). (2.8)
Из этого выражения следует, что суммарная геометрическая площадь ячеек насоса с учетом площади, занимаемой пластинами, численно равна площади кольца со средним радиусом R и толщиной 2е за вычетом площади, занимаемой выступающими частями всех пластин, т. е.
|
Рис. 27. Схема для расчета сечения ячейки с учетом толщины пластин |
|
ТТ |
F'w = 2e6Z.
Относительная толщина пластины обычно не велика. Если принять относительную толщину пластины в пределах
Б/R = 0,01 ... 0,075 (2.9)
(меньшие значения — для стальных пластин, а большие — для асботекстолитовых пластин), то
= BZ = 0,01 0,075 (j g 12 1Q_3Z Ph 2NR 2л V '
Как показывают расчеты, при применении стальных пластин уменьшение площади ячейки при Z 20 составляет не более 3 %, при применении неметаллических пластин и Z 8 —-не более 12 %. Поэтому часто уменьшение площади ячейки пластинами не учитывается, тем более что уменьшение объема ячейки над поверхностью ротора сопровождается увеличением точно такого же объема в его пазах. При вращении ротора освобождающийся объем паза заполняется газом на участке всасывания, а на участке сжатия и нагнетания газ вытесняется пластинами из пазов ротора. Эффективность использования дополнительных объемов в пазах ротора невысока, так как они соединены со всасывающим и нагнетательным патрубками в основном через узкие торцовые зазоры.
Изменение объема рабочей ячейки с радиальными пластинами при повороте ротора. Объем рабочей полости ячейки при данном угле поворота (м8)
V9 = FvL.
За угол ф поворота ротора принимают угол между биссектрисой А02 ячейки и линией 0г02, проходящей через центры цилиндра Ох и ротора 02 (см. рис. 24). Поскольку все ячейки насоса имеют одинаковую длину, то изменение объема ячейки будет прямо пропорционально изменению площади ее поперечного сечения. На рис. 24 площадь ячейки Fv заштрихована и обозначена цифрами 1234.
Площадь ячейки при угле поворота ротора ф (м2)
Ф+0.5Р Ф+0,50
F9 = J <*Ар = 0,5 J p*dq>(2.10)
<р —0.50 <р—0,5р
Текущий радиус-вектор (м)
Из треугольника 0i02Ј 02В = е cos ф;
|
■ sin2 - у; |
|
Из треугольники Из треугольника 0±0гА Sin "у = Я sin ф. (2-11) Тогда |
Из треугольника ОхВЛ В А = R cos у — R 7/1
|
(2.12) |
Из треугольника 0,02у4
Р = RY1 — Я2 э1п2ф + е cos ф.
Подставляя выражение (2.12) в уравнение (2.10), после преобразований и упрощений получим
Fy = - у - Я (2 — Я) /?2р -}- № sin р cos 2ф + , ЗД2
-Г-J. [sin (ф + -§-)У - Я2 sin2 (ф + 4) -
- sin (ф - 1 - Я2 Sin2 (ф - -§-)] +
-f-^-arcsin [я sin (ф + ~2~)] —■y-arcsin [Я sin ^ф---------------------- .
(2.13)
Учитывая, что для насоса, как правило, Я 0,18, можно принять
V — Я28Ш2ф » 1 —
При этом максимальная ошибка при ф = 90° и Я = 0,18 не превысит 0,0135 %. Следовательно,
Г*
Р»#(1 + Ясовф — (2.14)
Или
|
( |
1 К
-=- + cos ф-------- 2~sin^J. (2.15)
Подставляя выражение (2.14) или (2.15) в уравнение (2.10), после интегрирования площади текущей ячейки при данном угле поворота ф без учета толщины радиальных пластин получим
Fv = 2ЯЯ2 [ sin -§- cos ф + 4- sin р cos 2Ф + А (1 - ±) ] .
При Z > 12 и Р 30° с погрешностью не более 5 % можно принять
Sin Р « р и sin fa ;
Тогда
Fy я? ^ 1 - J - cos ф - J cos 2ф---------------------- =
==Я/?2р(1+С05ф--|-51П2ф)- (2.17)
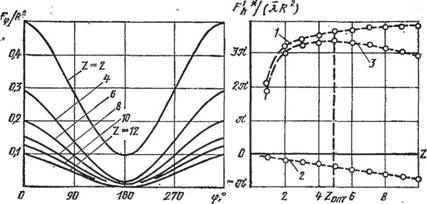
На рис. 28 представлено изменение площади ячейки при Я = 0,1 для различных чисел радиальных пластин. Площадь ячейки максимальна при ф = 0 и 360° и минимальна при Ф = 180°.
|
Рис. 28. Зависимость площади попереч - Рис. 29. Зависимость геометри - ного сечения ячейки от угла поворота ро - ческой площади ячеек ПРВН от тора для различных чисел Z пластин при числа Z пластин X = 0,1 |
Максимальную площадь Fh и минимальную площадь F0 ячейки можно определить по формулам (2.13), (2.16) и (2.17) при соответственно ф = 0 и ф = 180°:
Fh,О = 0,5Я (2 - Я) + 0,5№ sin р±
±W?2sin-§-]/l _ Я2 sin2 ± R2 arcsin ^ Я sin. (2.18)
При Я < 0,18
Fh, о « KR* (р ± 2 sin -§- + A - sin р - Щ) = ^г С. (2.19)
При Z> 12
Fh « 2ЯЯ2р = 4ice#/Z. (2.20)
Знак «-f-» в формулах (2.18) и (2.19) соответствует максимальной площади радиальной ячейки 1'2'3'4' (см. рис. 24), а знак «—» — минимальной площади ячейки 1"2"3"4". При ф = 0 выражения (2.6) и (2.18) тождественны, а формулы (2.5) и (2.20) совпадают.
Суммарная геометрическая площадь ячеек насоса с учетом толщины пластин согласно выражениям (2.2), (2.4) и (2.7) (м2)
FH = F*hZ = lR* (р + 2 sin + -§- sin P ~ "T") Z ~ 2e6Z - (2-21)
Оптимальное число пластин. Из выражения (2.21) видно, что с увеличением числа пластин Z первое слагаемое возрастает, а второе — уменьшается (кривые 1 и 2, рис. 29). Для нахождения максимальной суммарной геометрической площади ячеек насоса необходимо найти первую производную dF'h* dZ и приравнять ее к нулю. Разложив значения sin (3 и sin (Р/2) в ряд и взяв первые два члена ряда, получим
. о я Р3 2я (л 2 я2
S In ± »-L - -L (±У = JL (1 _ Ьш 2 2 31 V 2 / г I 6Zv •
Тогда
После дифференцирования получим
= ( + =
Опт
Для стальных пластин
ZonT = nf (2.22)
Изменение относительной суммарной геометрической площади ячеек зависит от толщины радиальных пластин (рис. 29 кривая 3). Данный расчет по оптимизации числа пластин не учитывает изменения внутренних перетеканий газа и мощности трения при различных числах пластин.
Число пластин в насосе влияет на быстроту действия, потребляемую мощность, температуру нагнетания, КПД, трудоемкость изготовления и надежность работы. Число пластин в насосе может изменяться от 2 до 20 и даже более. С увеличением числа пластин уменьшаются внутренние перетекания газа и разность давлений газа между двумя соседними ячейками; в то же время увеличивается мощность, затрачиваемая на преодоление сил трения, трудоемкость изготовления пазов ротора, а также износ корпуса насоса. Кроме того, число пластин определяется материалом, из которого они изготовлены. Металлические пластины имеют меньшую толщину по сравнению с неметаллическими пластинами (например, из асботекстолита) и, следовательно, их можно больше расположить в теле ротора без заметного снижения его прочности. Число пластин существенно сказывается на уравновешенности насоса (см. п. 2.6).
Влияние числа пластин на откачные и энергетические характеристики насоса проверяли экспериментально. При уменьшении пластин с 12 до 6 быстрота действия насоса РКВН-6 практически не изменялась. Уменьшение быстроты действия наблюдалось при четырех пластинах вследствие увеличения внутренних перетеканий газа, а монотонное снижение потребляемой мощности при сокращении числа пластин объясняется, в первую очередь, уменьшением мощности трения.
Ориентировочно число пластин следует выбирать в соответствии с данными, приведенными ниже.
Быстрота действия насоса, м3/с................................ До 0,1 0,1 ... 0,4 Св. 0,4
Пластины:
Неметаллические — текстолитовые (ПТ-7),
Асботекстолитовые (марки А), графитовые
(УГ-20к, АГ-150-Б-83), антифрикционная
Композиция (ФКН-7)......................................... 2...6 6 ... 8 8 ... 12
Стальные (сталь 85) .......................................... — — До 20
В насосе с увеличением разности давлений число пластин возрастает, так как необходимо уменьшить перепад давлений между ячейками. При увеличении размеров насоса в теле ротора можно расположить большее число пластин.
Эксцентриситет. Теоретическая быстрота действия насоса прямо пропорциональна эксцентриситету. Поэтому для лучшего использования объема цилиндра целесообразнее выбирать большие значения эксцентриситета. Однако размер эксцентриситета ограничен допустимой глубиной паза ротора и прочностью пластины. Обычно эксцентриситет (м) выбирается в пределах
Е = (0,10 ... 0,1875) R. (2.23)
С увеличением эксцентриситета возрастает угол у между направлением паза ротора и радиусом цилиндра (см. рис. 24), что может привести к заклиниванию пластин на угле сжатия. Поэтому чем выше отношение давлений, создаваемое насосом, и давление нагнетания, тем меньше должен быть вылет пластины из паза ротора во избежание большого изгибающего момента. Следовательно, необходимо принимать меньшее значение эксцентриситета.
Ширина пластины. Максимальный вылет радиальных пластин из пазов ротора составляет amsx = 2е (см. рис. 25). Чтобы в этом положении пластина имела необходимую устойчивость, оставшаяся ее часть в пазу ротора должна быть по крайней мере равна максимальному вылету. Из этих соображений для нормальной работы пластин ее ширину (м) обычно принимают
H = (3,5 ... 4,0) е. (2.24)
Подставляя выражение (2.23) в выражение (2.24), получим
H (0,35 ... 0,70) R. (2.25)
|
(2.26) |
Глубина паза ротора. Глубину паза ротора под пластину (см. рис. 22) во избежание опасности ее заклинивания и попадания под пластину продуктов изнашивания принимают (м)
= h + (0,0005 ... 0,001).
A) S)
Рис. 30. Схема действия сил при расчете на прочность ротора: а — с наклонными пазами; 6 — с радиальными пазами
У большинства выпускаемых в настоящее время насосов пазы ротора изготовляют с наклоном по отношению к радиусу ротора в сторону вращения на угол яр = 8 ... 15°. Насосы с наклонными пластинами имеют некоторые преимущества по сравнению с радиальными, а именно увеличивается ширина пластины, что приводит к улучшению условий движения пластины в пазу ротора и к уменьшению опасности ее заклинивания; повышается срок службы пластин и снижается мощность трения. Однако с увеличением угла наклона пластин возрастает изгибающий момент, действующий на пластину, и трудоемкость изготовления пазов ротора. Задавшись числом пластин и определив их размеры, необходимо проверить размещение пазов в роторе и рассчитать на прочность тело ротора. Схема действия сил, приложенных к телу ротора, ограниченного двумя соседними пазами, приведена на рис. 30. Опасным является сечение I—I. На выделенный элемент ротора действует центробежная сила Fc и реакции со стороны пластин RA и Rb. Нормальное напряжение (Па) в опасном сечении складывается из напряжений изгиба аи и растяжения ар:
6 (Rj. b — R.a + F^) Fr ° = + {в щ
Где а, Ь, с — соответственно плечи сил Ra, Rb и Fc, м; H0 — ширина опасного сечения, м; Fc — центробежная сила, Н, Fc = mcPcw2 (тс — масса элемента ротора, ограниченного пазами, кг; рс — расстояние от центра тяжести С элемента ротора до оси вращения ротора, м; со — угловая скорость ротора, рад/с).
Допускаемое нормальное напряжение для ротора, изготовленного из стали 40Х или чугуна СЧ 20, обычно не превышает [а] = = 1,0 МПа с учетом обеспечения жесткости элемента ротора. Число пластин, которые можно разместить в теле ротора, зависит от ширины, глубины паза и угла его наклона. Размещение пластин в теле ротора проще всего определить из чертежа на стадии проектирования насоса.
Ру/Ро
|
40 |
|
80 |
Рис. 31. Схема для определения угла Рис. 32. Зависимость давления газа ак сжатия в ячейке от угла <р поворота ротора
Длина роторов. С увеличением длины ротора увеличивается быстрота действия насоса. Однако при значительной длине ротора возникает опасность заклинивания пластин в пазу ротора. Кроме того, при большой длине корпуса необходимо предусматривать большие температурные деформации, приводящие к повышенным торцовым зазорам и перетеканиям газа. При неизменной быстроте действия насоса с уменьшением длины ротора возрастает его диаметр, что приводит к увеличению относительных перетеканий газа через зазоры между ротором и торцовыми крышками. Относительную длину ротора насоса обычно выбирают в пределах Кь = L/R = 3 ... 5.
Повышение давления газа в ячейке с радиальными пластинами. С увеличением угла ф поворота ротора уменьшается объем ячейки и соответственно возрастает давление газа, заключенного в ней (рис. 31). При политропическом сжатии газа без учета внутренних перетеканий
Pv(FvL)n = Po(FhL)n.
|
Ip=0 |
Откуда текущее значение давления газа в ячейке, согласно формулам (2.16) и (2.19), (Па)
Р + 2 sin + - g - sin р--------------- ^-Р
|
(2.27) |
|
Р<р = Ро |
|
Где р0—давление газа в начале сжатия, принимаемое равным давлению всасывания, Па; п — показатель политропы сжатия газа, принимаем для воздуха п = 1.4; ф — угол поворота биссектрисы ячейки, рад. |
Р + 2 sin - g - cos ф + sin Р cos 2ф--------------- ^- р
При Z> 12 с учетом формул (2.17) и (2.20) давление газа в текущей ячейке (Па)
Рф «РО(----------------------------- V- (2"28)
1 - f cos ф — sinBX ф '
Это уравнение может быть упрощено. Угол сжатия (см. рис. 24) а = ф + у. Тогда
Cos а = cos (ф + у) = = cos ф cos y — sin ф sin у.
|
Чения ячейки при наклонном расположении пластин в пазах ротора |
Так как значение угла Y мало, можно принять cos Y ^ С учетом уравнения (2.11) выражение (2.28) принимает вид
P^Po(L+2cosaT-
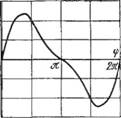
Изменение давления газа по сравнению с начальным давлением в ячейке зависит от угла поворота ротора (рис. 32).
При проектировании насоса часто решают обратную задачу, а именно определяют максимальный угол ак сжатия, соответствующий конечному давлению газа в ячейке рк. Принимая рф = рк, по уравнению (2.29) и рис. 31 находят угол ак (рад):
При малом числе пластин (Z < 12) максимальный угол фк поворота ротора, соответствующий концу внутреннего сжатия, (рад)
в ■ V I С —Л+ + B + C)D] /0 0„ч фк = arccos у (4cJ Н 2с |'
Где Л = р ^ 1-------- В = 2sin;
С-*--* * =
|
(2.29) |
При т > 4 угол сжатия ак > 100°. В этом случае значительно сокращается площадь нагнетательного окна и увеличивается скорость газа. Поэтому при большом значении т повышение внутреннего давления газа в ячейке сжатия выбирают в пределах не более PBJp = 4 ... 6 < т = рн/р.
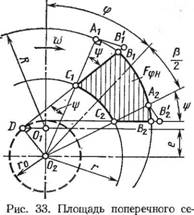
Изменение объема рабочей ячейки с наклонными пластинами при повороте ротора. Площадь Fm поперечного сечений ячейки с наклонными пластинами, ограниченная площадью фигуры С&В^Съ (рис. 33):
= FctBtBzCt — РсгА^с, — F AlBlCl + FAaBlC, = F<Q — AFy,
Где ДРф = FAiBlCl — FAiB^Ci.
При небольших углах гр наклона пластин площади фигур >41Б1С1 и Л2В2С2 приближенно равны площадям прямоугольных треугольников АВ[С и А2В2С2.
FAibiCi « FAiB. Ci = 0,5 (AiC{f Tg Ф;
FAtBTc. « FA2B'zC2 = °'5 ^
Из прямоугольного треугольника 02ОСг радиус вспомогательной окружности r0 = г sin 1]). Отрезки А1С1 = рх — г и А2С2 = — Рг — г> ГДе радиусы рх и р2 определяют из формулы (2.14) при Фх и ср2 соответственно, т. е.
Фх = ф — и Ф2 = Ф + -|*-
После упрощений и преобразований получим
AFq, = (4 sin ф sin + sin2ф sin р) .
При Z>12 sin«-jj - и sin Р л; р. Тогда
AFq, = (2 sin ф + sin 2ф). (2.31)
На рис. 34 приведена зависимость разности площадей ячеек с радиальными и наклонными пластинами, выраженная в безразмерной форме.
Относительная поправка разности площадей ячеек AFJF^ согласно (2.17) и (2.31):
Д^Ф _ X tg ty_____ 2 Sin ф + Sin 2ф____
F<p 2 . . , ^ о ^ ' 1 + cos ф + - у cos 2ф------------
График изменения AF^/F^ от угла ф поворота ротора представлен на рис. 35.
Из приведенного анализа можно сделать следующие выводы.
1. Максимальные объемы ячеек с радиальными и наклонными пластинами практически равны.
2. При сжатии и нагнетании газа (0 <С ф <С л) объем ячейки с наклонными пластинами несколько меньше по сравнению с ра
диальными пластинами при одном и том же угле поворота ротора, т. к. ДFy > 0. Следовательно, сжатие газа в ячейке с наклонными пластинами будет происходить более интенсивно. Однако в ряде случаев при проведении ориентировочных расчетов для i])-< 12° этими поправками, составляющими 2—3 %, можно пренебречь.
Давление газа в ячейке с наклонными пластинами при угле поворота ф (Па)
_ ( Fh Y Арн - Po{F(p_AFJ •
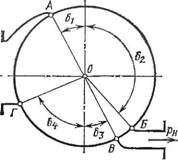
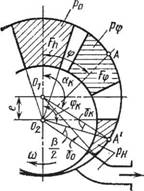
Выбор углов расположения кромок всасывающего и нагнетательного окон. Положение кромок всасывающего и нагнетательного окон корпуса А, Б, В и F (рис. 36) определяет продолжительность фаз газораспределения насоса. Верхняя кромка всасывающего окна (точка А) при радиальном расположении пластин определяется углом б] (рад):
Б1»0,5р(1 +Я).
Однако вследствие перетеканий газа ячейка заполняется газом несколько раньше, и поэтому угол практически принимается в пределах
8T = (0,6 ... 1,0) р.
Верхняя кромка нагнетательного окна (точка Б) определяется углом 62 (рад):
Для радиальных пластин (см. рис. 31)
О D
|
ZiF?/(e'JH3f)
|
|
Z 7 0 -7 -2 -3 Рис. 34. Зависимость поправки 2Д^ф/(е2Р tgij)) при определении площади поперечного сечения ячейки с наклонными пластинами от угла ф поворота ротора |
62 « фк + - гг + То = «к + + Yo - YK;
Для наклонных пластин
|
Тк + Я^, |
® Фк + -§" + Vo + Я^ = «к +
+-T + VO
Vo = arcsin sin (q>K + j j ; VK = arcsin (Я sin фк).
Для простоты расчетов часто принимают
Б2 « ак + (0,3 ... 0,5) р.
Нижняя кромка нагнетательного окна (точка В) определяется углом 63. При ф = 180° ячейка имеет минимальный объем и может быть отсоединена от нагнетательного окна, т. е. можно принять б3 = 0,5р. С учетом перетеканий газа 63 = (0,5 ... 1,0) р.
Положение нижней кромки всасывающего окна (точка Г) Определяется углом 64. При Z > 12 б4 = (1,5 ... 2,5) р, причем большие значения соответствуют большим отношениям давлений. При Z < 12 63 + 64 = (1 ... 2,5) р.
Определение основных размеров насоса. При заданной быстроте действия насоса 5 его геометрическую быстроту действия (м®/с) определяют по формуле
Sr = S/K
Где Я — коэффициент откачки.
После подстановки в уравнение (2.3) относительного эксцентриситета Я и относительной длины ротора Кь формула для определения геометрической быстроты действия принимает вид
Sr = C%KLR3n,
|
|
|
Где |
|
Рис. 36. Углы отсечных кромок всасывающего и нагнетательного окон |
Где R — радиус расточки корпуса, м; п — частота вращения ротора, с-1. Тогда
3 / - У а
CXKLi
Заменяя частоту вращения ротора скорость пластин и (м/с), получим
П = U/(2nR).
|
R |
|
На среднюю окружную (2.32) |
Тогда
|
R = |
|
(2.33) ■е = R (1 — |
2jtSr C%KLu
Остальные размеры (м) насоса: е = KR, Г = R — Я), L = KlR-
По формулам (2.9), (2.25) и (2.26) определяют толщину 6 пластины, ее ширину H и глубину Hn паза ротора.
Угловая скорость ротора (рад/с)
Со = 2п п. (2.34)
Коэффициент откачки в общем случае
Я — ЯдрЯ? — Яо — Яп — Ян>
Где Хдр — коэффициент дросселирования; Лт — коэффициент подогрева; %'0 — относительные потери быстроты действия, обусловленные обратным расширением газа; — относительные потери, обусловленные внутренними перетеканиями газа и переносом газа в изолированном объеме; К'н — относительные потери вследствие внешних натеканий атмосферного воздуха.
Как показывают результаты экспериментального и теоретического исследования насосов, коэффициент подогрева близок к единице (Ят л: 0,96 ... 0,99). Дроссельные потери также незначительны (Ядр л; 0,97 ... 0,98), потому что у насосов отсутствуют всасывающие клапаны, а скорость газа во всасывающем патрубке не превышает 25 м/с. Потери от обратного расширения газа составляют не более 3 ... 6 %, поскольку перевальный объем мал. Таким образом, при отсутствии или незначительных внешних натеканиях воздуха (Ян л; 0) коэффициент откачки в большой степени определяется внутренними перетеканиями газа и потерями с переносом газа в изолированном объеме
Я«(0,90 ... 0,95) — С
Относительные потери при внутренних перетеканиях газа
Яп = (/пи. о + mn)/(pBCSr),
Где ти. „— масса газа, переносимая в изолированном объеме в единицу времени, кг/с: тп — внутренние перетекания газа, кг/с; рвс — плотность газа на всасывании, кг/м3.
Внутренние перетекания газа в насосах происходят в основном через радиальные и торцовые щели, поскольку перетекания в пазах ротора весьма незначительны. На коэффициент откачки существенно влияет также изолированный объем. Например, если на углу б3 + 64 располагается три и более пластин, то возможен перенос газа в изолированном объеме с нагнетания на всасывание. При этом
Ти. о = Р., OZLnpn,
ГДе /"и. о — площадь изолированной ячейки, м8; определяют по формулам (2.13) или (2.16) при угле фи. 0 = 180° — 63 -f р/2; рн — плотность газа на нагнетании, кг/м3.
При б3 + б4 ^ 2|3 можно принять ти - 0 « 0.
В общем случае внутренние перетекания
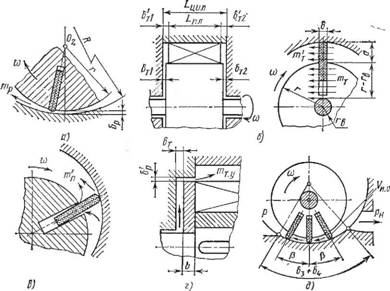
Тп = тТ 1 + тт2 + тТ + /пт2 + /пр + Шт. у> где тт1 и тт2 — массовый расход газа через торцовые щели, кг/с; т'т1 и — то же, между пластиной и торцовой крышкой, кг/с; тр — то же, через радиальную щель, кг/с; тт. у— то же, через дисковое торцовое уплотнение, кг/с.
|
Рис. 37. Типы щелей в насосе: А — радиальная; 6 — торцовая; в — микрощелевой зазор; г — в дисковом уплотнении; о — положение изолированного объема |
Торцовые перетекания преобладают над остальными внутренними перетеканиями и иногда составляют 50... 60 %. Очень хорошие условия для радиальных перетеканий создаются в щелях с плавно сходящимися и затем расходящимися стенками между ротором и корпусом в месте их наибольшего сближения. Кроме того, окружная скорость ротора совпадает по направлению с движением газа в радиальном зазоре.
Пути протеканий газа и типы щелей в насосе даны на рис. 37.
Известны методы снижения внутренних перетеканий газа и повышения КПД насосов: выбор оптимальных рабочих зазоров, скорости скольжения пластин по цилиндру, числа пластин и относительной длины ротора; постановка дисковых и торцовых уплотнений, изготовление проточки на цилиндре под ротором, перепуск газа, впрыск масла в рабочую полость и др.
Глубина щели в большой степени зависит от типа щели, т. е. от глубины дросселирования газа. По данным И. А. Сакуна, для радиальной щели между ротором и цилиндром (рис. 37, а) Относительная глубина
/ Ь _ 2Д)
ЫРЛ - 6Р'
Где бр — радиальный зазор, мм.
Длина радиальной щели / = L, а высота 6 = бр.
Глубина щели кольцевого уплотнения, выполненного в виде торцового диска (рис. 37, г), равна высоте b диска. Обычно Ь/бр > > 50. Длина щели I ж пг, а высота щели б = бр. Глубину торцовой щели между пластиной и торцовой крышкой (рис. 37, б) принимают равной толщине б пластины. Длина щели в общем случае / = р — г, а суммарная высота щели 2 б = бт1 + бт2 — = £цил — LnJl. Очень часто принимают 2 8 = 2Ь'Т.
Глубину торцовой щели в дисковом уплотнении принято условно с учетом диаметра вала считать как среднеарифметическую величину (мм):
Ь = & + Ьй + ... + Ьт)/т,
Где т — число расчетных интервалов.
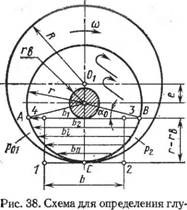
При этом площадь сегмента ABC заменяется на площадь прямоугольника 1234 (рис. 38) со стороной Ь (мм):
Ь = [г2 (0,5я — а0) — rrB cos а0 ]/(г — гв),
Где а0 = arcsin (rB/r), рад; гв — радиус вала, мм.
Длина торцовой щели I — г — гв, а высота щели б = бт. При этом считается, что в верхней части торцового зазора между ротором и крышкой (рис. 38) перетекание отсутствует, так как газ течет из торцового зазора в основном в ячейки, изолированные от всасывающего патрубка.
Расход газа через радиальную щель (кг/с)
Щ = <7р6Р^>
Где <7Р — удельный расход газа через радиальную щель, кг/(м2-с).
Расход газа через торцовую щель между ротором и торцовой крышкой (кг/с)
ТТ = <7Т бт (г — гв),
Где qT — удельный расход газа через торцовую щель между ротором и торцовой крышкой, кг/(мв-с).
Расход газа через торцовую щель между пластиной и торцовой крышкой (кг/с)
Т т = <7тбт (р — г),
|
Бины торцовой щели |
Где Q'T — удельный расход газа через торцовую щель между пластиной и торцовой крышкой, кг/(ма-с).
|
20 |
|
3D |
|
Л О, в 0,6 0£ 02 о |
|
|
|
W |
W
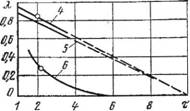
Рис. 39. Зависимость коэффициента % откачки от отношения давлений т для
Различных вакуумных насосов: I — РВН-50; 2 — РВН-25; 8 — РВН-6; 4 — PRBH-6; 5 — РКВН-9; 6 — PBH-40/3S0
Уплотняющий эффект дискового уплотнения достигается в результате потерь энергии на преодоление трения газа при течении его в глубокой щели, а также лабиринтного действия уплотнения. Газ дважды проходит узкую щель бр, а после щели затормаживается сначала в полости торцового зазора, а затем в полости всасывания.
Внутренние перетекания газа через различные типы щелей в насосах определяют по методике, изложенной в гл. 3.
Для приближенных расчетов коэффициент откачки обычно принимают равным К fa 0,6 ... 0,8. Наибольшее значение коэффициента К следует выбирать для насосов, работающих с подачей масла в цилиндр, а также для вакуумных насосов большой быстроты действия с невысоким отношением давлений.
Значение коэффициента откачки зависит от отношения давлений для различных насосов. На рис. 39 штриховой линией показана характеристика вакуумного насоса при кратковременной работе. Как видно из приведенных характеристик, в связи с увеличением отношения давлений коэффициент откачки уменьшается практически по прямой.