Машины, работающие по циклу Стирлинга
РЕЗУЛЬТИРУЮЩИЕ ГРАФИКИ
Несмотря на всю пользу приведенных на рис. 5-5 диаграмм, легко представить, что существует бесконечное множество различных сочетаний конструктивных параметров. Искать варианты оптимальных сочетаний параметров — дело утомительное. Для преодоления указанных трудностей строятся результирующие графики, подобные тем, что приводятся соответственно для двигателей на рис. 5-7 и для холодильных машин на рис. 5-8.
|
|
|
Х=0,1; 0,25; 0,5; 1,0; |
|||||||
|
1 |
|||||||
|
I |
|
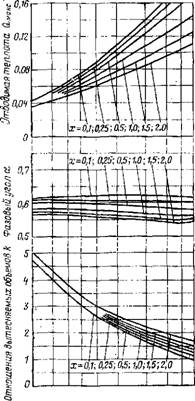
Рис. 5-8. Результирующие графики для холодильных машин с циклом Стирлинга. |
|
3»«Ff 'A |
|
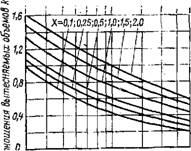
30 40 . 50 60 75 100 150 200 "3Q0 Температура, полости расширения^,К |
|
G 300 500 1000 1500 2000 3000 Температура полости расширения Te, К Рис. 5-7. Результирующие графики Для двигателей Стирлннга. Оптимальная комбинация из отношения вытесняемых объемов k и фазового угла а (в радианах) может быть определена для заданных значений отношения мертвого объема X и Ьтиошеиия температ. ур X по вертикальным линиям, проведенным иа графиках через значения температуры Tg' считается, что температура. Тg — 300 К. а ТЕ ограничена термическим пределом материалов, используемых для цилнидра полости расширения. Соответствующее значение параметра мощности определяется по верхнему графику. В реальных двигателях параметр мощности составляет 0,3—0,4 значения, предсказываемого теорией. |
Значения параметра холодопронзво - дительиости, характеризующегося количеством теплоты, поглощаемой в полости расширения, отличаются от его действительных значений приблизительно в 3 раза.
Графики на рис. 5-7 построены с использованием оптимизации по параметру P/puaKCVT. Для указанного параметра при различных значениях а и k и постоянных т и X были образованы поверхности, подобные приведенным на рис. 5-5. Далее были определены вершины каждой из поверхностей, и эти значения, характеризующие максимум параметра P/pMaKCVT, вместе с аопт и konr наносились на соответствующие диаграммы рис. 5-7. Все эти графики были построены в зависимости от температуры полости расшире
ния; температура полости сжатия, равная 300 К, принималась Всегда постоянной. Затем были определены и нанесены на графики вершины поверхностей для различных значений т и X. Подобный метод был применен и для получения аналогичных графиков для холодильных машин, оптимизированных по параметру холодо - производительности QЈ/pMaKCVr (см. рис. 5-8).
Работа по определению координат вершин поверхностей для любых постоянных значений т и X и при начальных параметрах а и K выполнялась с применением самооптимизирующей цифровой ЭВМ по программе, созданной с использованием метода наибыстрейшего спуска, описанцого Уокером в 1962 г.
Применение для конструирования результирующих графиков
Графики, приведенные на рис. 5-7 и 5-8, рекомендуется использовать на предварительных стадиях конструирования машин с циклом Стирлинга.
В случае двигателя необходимо, во-первых, установить допустимую температуру ТЕ для полости расширения. Она определяется природой теплового источника и теми конструкционными материалами, которые могут быть применены для теплообменников и цилиндра полости расширения. При выбранных значениях температуры ТЕ на трех графиках проводятся вертикальные линии. Из графиков по точкам пересечения вертикальных линий с сетками кривых для выбранных значений отношений мертвого объема можно определить соответствующие оптимальные значения фазового угла а и отношения вытесняемых объемов K. Аналогичным образом может быть определено и значение параметра мощности P/pMaKCVT. Поскольку ТЕ известно, а Тс принимается (значение этой температуры в двигателе с водяным охлаждением приблизительно равно 300 К), то может быть рассчитан и параметр Я/рмаксУг. Таким образом, зная т, X, а и K и используя краткий перечень приведенных выше уравнений, можно перейти к непосредственному конструированию двигателя.
Нельзя не отметить, что расчетные данные, полученные для цикла по теории Шмидта, весьма оптимистичны. Как показывает опыт, нельзя ожидать от реального двигателя значений мощности и эффективности, составляющих более 30—40%, предсказываемых по теории Шмидта.