ВЫСОКОПРОЧНЫЙ БЕТОН

ОСОБЕННОСТИ ВЗАИМОСВЯЗИ МОДУЛЯ УПРУГОСТИ И ПРОЧНОСТИ БЕТОНА

Полученное выражение (V.15) дает возможность сфор­мулировать общее положение о характере зависимости меж - ду упругими и прочностными свойствами тяжелого бето­на. Особенность этой связи заключается в том, что оца не является однозначной и ее вид определяется, по крайней мере, еще двумя конкретными характеристиками бетона — содержанием цементного теста в смеси и упругими свойст­вами использованного заполнителя.

Таким образом, в координатной системе Ех — Rx вы­ражение (V.15) описывает некоторую область, границы которой определяются изменчивостью обеих указанных характеристик бетона. Ориентируясь на реальные для тя­желого бетона пределы колебания величин Е3 = (4-f-6)105 и рт = 0,15^-0,30, можно убедиться из рис. 42, что в ре­зультате этого модуль упругости бетона Ех при неизмен­ной прочности Rx может изменяться более чем в полтора раза. Если же одновременно рассматривать и песчаные бетоны (растворы), у которых обычно рт > 0,3, то область возможных значений Ех еще более расширяется за счет смещения ее нижней границы. При рт = 1 выражение (V. 15) переходит в зависимость для чистого цементного камня (показана на рисунке пунктиром).

Любая эмпирическая зависимость для модуля упру­гости бетона в виде (V.4), т. е. в функции только прочности бетона, является одним из частных случаев выражения (V.15) при определенных фиксированных значениях па­раметров ф = const (т. е. Е3 = const) и рт = const [111]. Это следует из сопоставления формул (V.15) и (V.4), ко­торые связаны соотношениями:

Для тяжелого бетона на крупном заполнителе при из­менении £3иртв указанных ранее границах числовые зна-

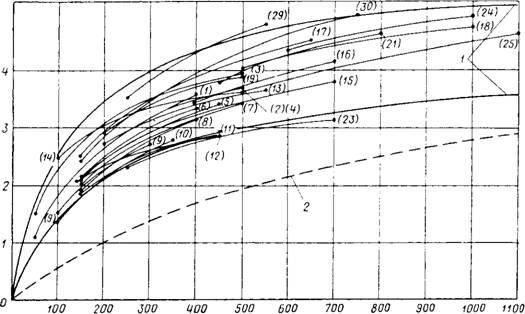
Рис. 42. Изменчи­вость корреляцион­ных связей между модулем упругости и прочностью тя­желого бетона по эксперименталь­ным данным (циф­ры в скобках соот­ветствуют номерам групп серий испы­таний по табл. 6)

/—пределы изменения модуля fy пру ГОСТИ по выражению (V.15) для тяжелых бетонов на крупном заполни­теле; 2 —то же, для чистого цементого камня

Чений коэффициентов Ёт и S в формулах типа (V.4) варьи­руются в весьма широких пределах: Ет = (4,1-7-5,8)105 и s = 100—300. Для песчаных растворов эти значения еще больше. Для цементного камня SK = 800; это предель­ная величина.

Разнообразные сочетания характеристик £3 и рт, ко­торые могут встретиться на практике, обусловливают по­этому существование бесчисленного множества частных зависимостей Ех = F(Rx), описываемых выражением (V.15). Примером может служить изменчивость корреляционных связей Ех = F(Rx) для бетонов на крупном заполнителе, наблюдаемая в большом числе экспериментов (см. рис. 42). Хотя каждая из корреляционных кривых, соответствую­щая группе серий испытаний (при Е3 ж const и рТ «

Const), сама по себе достаточно устойчива (см. табл. 6), совокупность этих кривых покрывает фактически обшир­ную область, определяемую на рис. 42 выражением (V.15).

Попытка аппроксимировать такое многообразие связей на рис. 42 в виде некоторой общей зависимости (в функции только прочности бетона) приводит, естественно, к резкому возрастанию разброса опытных величин по отношению к расчетным. В сравнении с большинством частных корреля­ционных связей среднеквадратичное отклонение в этом слу­чае увеличивается, по крайней мере, в 3—5 раз.

Поэтому нормирование модуля упругости в функции только его прочности обеспечивает сугубо ориентировочную оценку искомой величины. Большинство обычно предла­гаемых зависимостей типа (V.4) (см. табл. 5) не выходит за пределы все той же области на рис. 42, а расхождения в числовых значениях коэффициентов Ет и S (см. табл. 5) свидетельствуют лишь о том, что они получены для бетонов, индивидуальные характеристики которых в среднем не были одинаковы. Степень этих различий, установленная на основе соотношений (V.16) и (V.17), отчетливо видна из табл. 7.

Поскольку любая из зависимостей в форме (V.4) спра­ведлива, как это следует из табл. 7, только при наличии определенного заполнителя и при его неизменной дозиров­ке в бетонной смеси ни одну из них нельзя считать уни­версальной. Не случайно поэтому эмпирические формулы, рекомендуемые специально для песчаных бетонов (см. табл. 7), отражают характерное для них по сравнению с обычными бетонами повышенное содержание цементного теста рт.

Данные табл. 7 позволяют не только объяснить су­щество расхождений между различными предложениями, но и сразу судить об их характерных особенностях и недо­статках. Выясняется, например, что часто используемая формула Графа, в принципе вообще неприменима для со­временных тяжелых (тем более высокопрочных) бетонов, которые отличаются существенно более высокими средними значениями рт (см. табл. 7, данные СНиП и СН 365-67). Рекомендации СНиП для песчаных растворов неправильно интерпретируют их главное отличие от бетонов, дифферен­цируя лишь значения коэффициента Ет. В результате дан­ные СНиП отражают искусственно заниженные величины модуля упругости заполнителя (Е3 = 3,65 • 105), хотя фактически у кварцевого песка он в среднем не ниже, чем у гранита (см. предложение Роша).

Влияние обоих рассмотренных факторов наряду с проч­ностью на величину модуля упругости бетона само по себе не является неожиданным. Оно обнаруживалось в разное время в ряде экспериментов [98, 119, 129, 143, 160, 164]. Однако полученное выражение (V.15) впервые дает воз­можность разделить это влияние в количественном отно­шении и оценить его независимо одно от другого.

Все три характеристики бетона (RXf Е3 и рТ) слабо свя­заны друг с другом и могут встречаться практически в произвольных сочетаниях. Поэтому выражение (V.15) по­зволяет описать некоторые закономерности, которые никак не отражаются в существующих методах оценки величины модуля упругости бетона. Сказанное подтверждается ре­зультатами ряда экспериментов [119, 138, 165, 185 и др.].

Опыты Рюша, Кордины и Гильсдорфа [165] —тот ред­кий случай, когда модуль упругости заполнителя варьи­ровался в широких пределах и непосредственно измерялась его величина (табл. 8). Две другие исходные характери­стики — кубиковая прочность бетона и содержание цемент­ного теста в смеси — сохранялись практически неизмен­ными. Возраст бетона при испытании составлял 28 суток. В табл. 8 сопоставлены результаты прямых измерений мо­дуля упругости бетонов на разных заполнит елях и расчета этих величин по формуле (V.15).

Из табл. 8 видно, что хотя расчетные значения во всех случаях несколько выше опытных, они полностью отра­жают экспериментальную закономерность, которая обна­руживается при практически возможном изменении упру­гих свойств заполнителя. И опытные и расчетные значения модуля упругости бетона могут отличаться за счет только этого фактора почти в 4 раза. Данные СНиП, приведенные для сравнения, отражают в тех же условиях лишь незна­чительное влияние колебаний прочности бетона на модуль упругости.

Другой пример, заимствованный из опытов Боломея [119], когда при неизменной прочности бетона и исполь­зовании одинакового заполнителя в широких пределах варьировалось содержание цементного теста в бетонных смесях, приведен в табл. 9. Возраст бетона при испытании составлял 90 суток.

Можно убедиться, что выражение (V.15) и в этом случае хорошо отражает экспериментальные закономерности, сво-

Дящиеся к изменению модуля упругости бетона почти в 1,5 раза при неизменной его прочности за счет только влияния содержания цементного теста. Как и ранее, реко­мендации СНиП не учитывают возможность столь сущест­венных изменений.

На практике обычно одновременно изменяются не одна, а сразу две (чаще всего Rx и рт) или даже все три харак­теристики бетона, определяющие величину его модуля уп­ругости. Это может привести к полному нарушению обще­принятых закономерностей связи между модулем упру­гости и прочностью бетона (см. рис. 35). Указанные яв­ления, необъяснимые с точки зрения существующих под­ходов к оценке упругих свойств бетона, находятся, однако, в полном соответствии с характером выражения (V. 15). В табл. 10 сравниваются средние величины модулей упру­гости, полученные в упомянутых опытах, и его расчетные значения, вычисленные по формуле (V. 15).

Как видно из табл. 10, выражение (V. 15) во всех случаях правильно описывает достаточно сложные закономерности изменения модуля упругости бетона, наблюдаемые в рас­сматриваемых экспериментах и состоящие в заметном (до 20—27%) падении величины модуля при повышении прочности сверх некоторого предела.

На основе выражения (V. 15) это явление легко объяс­нимо и представляется вполне закономерным. Увеличение прочности бетона достигалось в опытах при одновременном росте содержания цементного теста в смесях. Поскольку такое изменение обоих факторов прямо противоположно отражается на величине модуля упругости бетона, характер получаемых связей с прочностью может быть самым раз­нообразным. Как правило, начиная с некоторого значения

Прочности, дальнейшее ее повышение не может компенси­ровать влияния растущего содержания цементного теста. Поэтому модуль упругости, достигнув максимальной вели­чины, начинает снижаться. Получаемая закономерность прямо противоположна той, которая предусматривается в этих случаях рекомендациями нормативных документов.

Таким образом, выражение (V. 15), являясь в значи­тельной мере универсальным, отвечает одновременно и теоретическим представлениям, и результатам большого числа экспериментов. С этой точки зрения оно имеет бес­спорные преимущества перед существующими эмпирически­ми формулами для расчета модуля упругости бетона и мо­жет быть использовано для практической оценки ожида­емых величин модуля упругости обычного бетона, цемент - но-песчаного раствора и даже чистого цементного камня

Ёйе зависимости of прочностных характеристик этих ма­териалов (во всяком случае до прочностей порядка 1000 кГ/см2). Выражение (V.15) позволяет также учесть некоторые специфические закономерности изменения модуля упругости бетона (раствора) в самых различных условиях. Все это открывает реальные пути повышения надежности прогнозов упругих характеристик бетона при проектиро­вании конструкций.