Прогрессивные технологии сооружения скважин
ПРОБКООБРАЗОВАНИЕ
Основной недостаток наиболее широко применяемых в практике технологий доставки гравия в интервал формирования обсыпки через кольцевое пространство скважины и вспомогательную колонну труб — пробкообразование. Образование гравийной пробки выше интервала сооружения фильтра приводит сначала к ограничению, а затем и прекращению поступления частиц в зону
411
Продуктивного пласта. При зависании гравия выше продуктивного пласта каркас фильтра непосредственно контактирует с песком, что обусловливает аварийное состояние скважины. Ликвидация пробок требует значительных затрат времени и средств, а в некоторых случаях приводит к необходимости переоборудования скважины.
Целесообразно в процессе сооружения гравийного фильтра ориентироваться на технологию, обеспечивающую предупреждение пробкообразования, а не на планирование дополнительных мероприятий по ликвидации пробок. Глубокие скважины практически не оборудуются гравийными фильтрами. Имеется единичный опыт сооружения гравийных фильтров в глубоких скважинах, что свидетельствует о непосредственной связи механизма пробкообразования не только с глубиной скважины, но и с рядом других факторов, влияние которых на процесс транспортировки гравия в зону фильтра пока не определено.
В отечественной и зарубежной литературе нет работ, специально посвященных процессам образования гравийных пробок в вертикальных потоках жидкости, что вызывает необходимость в проведении анализа имеющихся разработок в смежных областях знания. Очевидно, что процесс пробкообразования определяется закономерностями перемещения твердых частиц в потоке жидкости, которые рассматриваются в теории промывки скважин, гидравлического и пневматического транспорта, обогащения и гидравлической классификации материалов в потоках, гидравлики движения наносов в открытых руслах, теории гидродинамики, массопередачи, а также псевдоожижения и теории фонтанирующего слоя.
По мнению автора, процесс образования гравийных пробок может протекать двумя путями. Первый заключается в формировании гравийной пробки в некотором сечении кольцевого пространства скважины, в котором концентрация частиц гравия со временем увеличивается. Формирование пробки происходит в три этапа (рис. 8.11).
На первом этапе на некотором участке АВСД потока происходит зависание мелкой фракции гравия, а частицы больших размеров, проходя сквозь слой мелких частиц, свободно осаждаются в зоне фильтра (см. рис. 8.11, а). На втором этапе число зависших в зоне АВСД мелких частиц увеличивается, достигая критических концентраций, когда сначала затрудняется, а затем и прекращается миграция сквозь слой мелких частиц крупных фракций гравия (см. рис. 8.11, б). На последнем этапе формирования пробки весь закачанный в скважину гравий не поступает в зону фильтра, а зависает над участком АВСД (см. рис. 8.11, в). 412
|
Рис. 8.11. Формирование гравийной пробки |
Очевидно, что первый вариант формирования гравийной пробки носит узкий характер, так как может объяснить пробкообразование только в восходящем потоке жидкости. Поэтому наиболее справедливым следует считать второй вариант, заключающийся в предположении о формировании гравийной пробки от границ потока к его центру (см. рис. 8.11, г, д, е). В начальный период закачки гравия некоторые частицы под влиянием ряда причин стремятся переместиться от центра к границам потока,
413
Где скорость движения жидкости близка к нулю и частицы налипают или зависают на поверхности обсадных или фильтровых труб (см. рис. 8.11, г).
На втором этапе формирования пробки (см. рис. 8.11, д) частицы гравия прижимаются не к стенкам труб, а к уже зависшему на них гравийному материалу. Со временем толщина налипшего слоя увеличивается и достигает критических значений, когда закачиваемый в скважину гравий зависает над налипшим слоем и не поступает в зону фильтра (см. рис. 8.11, е).
Механизм формирования гравийной пробки по первому варианту (см. рис. 8.11, а, б, в) просто объясняется с позиций гидравлики. Второй вариант, предполагающий формирование гравийной пробки за счет перемещения частиц от центра к границам потока, позволяет объяснить пробкообразование в потоках любого направления и поэтому представляет наибольший интерес. Прижатие и налипание частиц на стенки труб и скважины будет наблюдаться при условии, если суммарное воздействие активных сил, приложенных к частице, сместит ее от центра к границам потока. Рассмотрим теоретические обоснования исследований механизма перемещения частиц в направлении, перпендикулярном направлению потока, предложенные различными исследователями.
В теории промывки скважины отмечается, что образование сальников в кольцевом пространстве - явление широко распространенное. Г. Цайдлер, проводивший исследования на специальном стенде, свидетельствует, что некоторые частицы налипают на стенки скважины и не выносятся на поверхность даже при форсированных режимах промывки. Таким образом, ученый доказал, что на вынос частиц из скважины влияет не только величина скорости потока, но и другие факторы.
A. К. Козодой и другие исследователи считают, что на частицу шлама при промывке действуют три силы: вес, сила Архимеда и сила сопротивления. Очевидно, что все эти силы направлены по оси вертикального потока и не могут вызвать перемещение в перпендикулярной плоскости. Поэтому предложенное теоретическое объяснение перемещения частиц в потоке не объясняет пробко - и сальникообразование.
B. Г. Беликов объясняет перемещение частиц в горизонтальной плоскости влиянием силы Жуковского, возникающей за счет различной скорости обтекания по противоположным от вертикальной оси симметрии сторонам частицы из-за наличия градиента скорости по сечению потока. Скорость потока увеличивается от границ к ядру, принимая максимальные значения в центре симметрии потока, и сила Жуковского при любом положении 414 Частицы в потоке пытается сместить ее в центр, где величина действующей горизонтальной силы снижается до нуля. Следовательно, предложенная теория не только не объясняет процесса налипания частиц на стенки потока, а скорей наоборот, доказывает его невозможность, чем противоречит многочисленным практическим данным.
В. Ф. Роджерс определяет механизм перемещения частиц в потоке либо законом Стокса, либо законом Риттингера (в зависимости от режима движения), которые не позволяют оценить перемещение частиц в плоскости, перпендикулярной направлению вертикального потока.
Специалистами по гидро - и пневмотранспорту механизм движения частиц рассматривался в основном применительно к горизонтальным потокам. В. М. Карасик считает, что на частицу в потоке действуют подъемная сила Жуковского; подъемная сила, вызванная турбулентной пульсацией, пульсация давления, сила веса, сила лобового давления, сила трения при обтекании жидкостью частицы. Из вышеперечисленных сил применительно к вертикальному потоку жидкости горизонтальное смещение может вызвать только сила, вызванная турбулентной пульсацией. Однако величина и направление турбулентных пульсаций постоянно хаотически изменяются и поэтому, если в некоторый момент времени частица за счет одной турбулентной пульсации перемещается к границе потока, то под действием другой, имеющей противоположное направление — переместится наоборот к центру потока. Кроме того, установлено, что в потоке преобладают вихри, закручивающиеся от границ к центру потока и, следовательно, вызывающие преимущественное перемещение частиц от границ потока к его центру.
A. Е. Смолдырев считает, что на частицу в потоке действуют четыре силы, а именно: сила тяжести без учета Архимедовой силы; подъемная сила Жуковского; сила гидродинамического давления и сила молекулярного взаимодействия. Очевидно, что действие вышеперечисленных сил применительно к вертикальному потоку не может объяснить пробкообразования.
B. И. Муштаев и другие авторы, рассматривая механизм движения частиц в закрученном потоке газа, выделяют следующие действующие на частицу силы: центробежная; гидродинамического сопротивления; тяжести; переносная Кориолисова; подъемная Жуковского; подъемная Архимедова. При взаимодействии частиц со стенками потока и другими частицами добавляются силы: трения качения; удара частицы о стенку; удара частицы о другую частицу. Горизонтальное смещение частицы к границам потока можно объяснить либо центробежной силой, либо силой
415
Удара частицы о другую частицу. В процессе доставки гравия в скважину поток гравийной смеси не закручивается и центробежная сила равна нулю. Закачку осуществляют при концентрации гравия в потоке менее 15 %, что свидетельствует об отсутствии взаимодействия между частицами. В связи с этим, ни центробежная сила, ни сила взаимодействия частиц друг с другом не позволяют описать механизм пробкообразования.
В теории гидравлической классификации движение частиц в потоке рассматривалось многими специалистами. Б. В. Кизеваль - тер выделяет следующие действующие на частицу силы: тяжести; Архимеда; сопротивления для равномерного движения частицы; дополнительная составляющая сопротивления, вызванная ускоренным движением частицы в потоке. Ни одна из четырех сил не может способствовать смещению частиц к границам потока.
Г. К. Смышляев и Г. Д. Краснов учитывают только силы веса, сопротивления и гидравлического давления, что также явно не достаточно для объяснения механизма налипания частиц на стенки скважины и труб.
В теории движения наносов в открытых руслах рассматривается механизм взвешивания частиц под действием подъемных сил Жуковского и турбулентной пульсации. Теория псевдоожижения и фонтанирующего слоя рассматривает стесненное движение частиц, учитывающее силу тяжести, гидродинамическое давление и влияние частиц друг на друга в зависимости от их концентрации.
К. Матур отмечает, что при обтекании частицы возникает отрыв потока, который может оказать существенное влияние на перемещение частицы. Однако такое утверждение противоречит данным, полученным П. Чженом. Он доказал, что отрыв потока может быть ликвидирован за счет вращения частицы. Аналогичный вывод ранее сделал Прандтль. Отрыв потока наблюдается за жестко закрепленной в потоке частицей, что соответствует методике эксперимента. При возможности свободного перемещения частицы она вращается, что способствует ликвидации отрывного течения. Устранение отрыва потока за счет вращения частицы вытекает из энергетической теории гидротранспорта, согласно которой при движении частицы в потоке потери энергии в системе жидкость — твердое тело стремятся к минимуму. При отрыве потока сопротивление обтеканию тела возрастает в среднем на 14,5 % и поэтому частица вынуждена поворачиваться или вращаться с целью устранения отрыва потока, что обеспечивает минимум потерь напора при транспортировке твердого.
В. Г. Беликов считает, что перемещение шлама от центра к границам потока объясняется вращением частиц. С другой сто - 416 Роны, Г. Цайдлер отмечает, что вращение частиц в потоке носит временный характер, а в пристенной области частицы не вращаются совсем. К. Матур и Н. Эпстайн показывают, что в фонтанирующем слое вытянутые частицы движутся без вращения.
Из представленного каждого обзора следует, что существующие теории не объясняют механизма перемещения частиц от центра к границам потока, их налипание на стенки, т. е. процесс пробкообразовзния.
Наряду с отсутствием прямого объяснения механизма образования пробок существуют экспериментальные работы, позволяющие косвенно судить о горизонтальном распределении частиц в вертикальном потоке. Многими исследованиями доказана связь между скоростью движения частицы в вертикальном потоке и ее формой.
В. Г. Волков предлагает ввести в формулу Риттингера эмпирический коэффициент, учитывающий зависимость скорости движения частиц от их формы. Значения коэффициента изменяются от 27,3 (для округлых зерен) до 19,7 (для плоских зерен). Для шара данный коэффициент равен 44,29 (по Риттингеру) или 55 (по Люону). Монроэ установил, что чем неправильнее форма частиц, тем меньше скорость их падения в потоке. Для шара скорость падения частиц равна скорости витания, т. е. соответствует значениям, рассчитанным по формуле Риттингера.
В ИГД АН СССР опытным путем установили, что происходит расслаивание частиц в зависимости от их формы. И. Ф. Де - видсон и Д. Харрисон показали, что скорость витания зависит от фактора формы частиц. К аналогичному выводу пришли Л. Аб - рагам, П. Пизо, Ф. Чинкабилла и С. Фаббри, К. Хейсканен.
В теории гидравлической классификации материалов также отмечена связь между скоростью падения частиц и их формой. Однако эта зависимость устанавливается не дополнительным коэффициентом, а считается, что коэффициент сопротивления обтеканию в формуле Риттингера — это функция формы частиц и кривые Рабея, построенные для одинаковых чисел Рейнольдса, но для частиц различной формы, не совпадают друг с другом.
Н. С. Григ и Р. И. Рэтбан приводят результаты исследования скорости падения частиц различной формы. Кривые зависимости скорости падения от диаметра частиц различной формы сравнивались с кривой Рабея, построенной для сферичных частиц, и при этом отмечалось, что причина несоответствия значений, полученных по формуле Рабея и данных доклада неизвестна.
Скорость витания частиц определяется по известным формулам на основании средней скорости потока, но на частицу в потоке действует сила гидродинамического давления, пропорцио-
417
Нальная квадрату не средней, а местной скорости в точке, в которой находится частица. Поэтому скорость выноса частиц зависит от положения частицы в потоке и чем ближе частица находится к границе потока, тем меньше скорость ее движения в восходящем потоке.
Принимая во внимание, что скорость транспортировки частиц потоком зависит от формы, разумно предположить, что частицы по сечению потока распределяются в зависимости от формы. Чем более сплющена частица, тем ближе она располагается к границе потока. Очевидно, что при определенной форме (назовем ее критической) частицы прижимаются к стенкам потока, налипают на них, образовывая пробки. В связи с этим фактор формы может определять перемещение частиц от центра к границам вертикального потока.
Смещение частиц к границам потока, их налипание на стенки - необходимое, но не достаточное условие пробкообразования. Наряду с механизмом налипания частиц на границы потока для образования пробок необходимо, чтобы первичный контур пробки сохранял свою устойчивость и не разрушался в потоке жидкости. Работы, посвященные устойчивости гравийных пробок в кольцевом пространстве скважины, не известны. Устойчивость свода сыпучих пород над кровлей горной выработки рассматривалась М. М. Протодьяконовым. Предложенная теория не позволяет оценить механизм разрушения свода равновесия при наличии фильтрации жидкости через сыпучую породу. Интересные исследования проведены Н. Стейном относительно возможности образования устойчивых арочных песчаных структур около отверстий фильтра. Н. Стейн опытным путем показал, что устойчивость песчаных арок сохраняется только при ламинарном притоке из пласта. В турбулентном потоке своды равновесия быстро разрушаются. Очевидно, что использование предложенной методики оценки устойчивости арочных структур применительно к гравийным пробкам в кольцевом пространстве скважины некорректно, так как в первом случае наблюдается радиальная фильтрация, a с последнем — плоскопараллельная. Кроме того, Н. Стейном не предложено количественной оценки устойчивости арочных структур.
Итак, для образования гравийных пробок необходимо наличие либо восходящего потока в кольцевом пространстве скважины, либо условий, при которых частицы гравия стремятся сместиться из центра к границам потока, где они зависают на стенках скважины или обсадных труб. Смещение частиц к стенкам, их налипание и зависание — необходимое, но недостаточное условие пробкообразования. Предупредить пробкообразование 418 Можно в случае разрушения образовавшихся структур пробки в потоке. Механизм пробкообразоеания за счет налипания частиц на стенки и характер устойчивости структур пробки объяснить на базе имеющихся работ невозможно, в связи с чем автор считает необходимым привести теоретические основы механизма пробкообразования, которые могут послужить основой для разработки новой техники и технологии, модернизации имеющегося оборудования.
Пробкообразование в ламинарном потоке жидкости
В процессе доставки гравия на забой скважины через кольцевое пространство частицы движутся преимущественно в ламинарном потоке. Ламинарный режим устанавливается при малых скоростях движения жидкости (до 0,1 м/с), для восходящего потока ограниченными возможностью выноса или зависания частиц гравия, а для нисходящего потока — производительностью откачного оборудования.
Рассмотрим движение сферичных гравийных частиц в ламинарном потоке в направлении оси х, перпендикулярной вертикальному потоку жидкости. Дифференциальное уравнение движения частицы имеет вид
D г=п r r r
- (mvx) = Z Fx = Fk1 + + Fc, (8.12)
Dt г=1
Где t — время; m — масса частицы; vx — скорость частицы в направлении оси х; Fx — проекция силы на ось х; FX1 — первая
Составляющая подъемной силы Жуковского; Fra — сила гидродинамического давления; FG — сила сопротивления.
Первая составляющая силы Жуковского FX1 возникает за
Счет наличия циркуляции скорости Г по контуру гравийной частицы. Циркуляция скорости Г по контуру частицы наблюдается при наличии изменяющегося по сечению градиента скорости потока. Скорость обтекания частицы по ее противоположным относительно вертикали сторонам различна, и, соответственно, согласно уравнению Бернулли различно и давление, действующее на противоположные стороны частицы (рис. 8.12). Скорость обтекания поверхности частицы, направленной к центру потока, всегда больше, чем скорость обтекания поверхности, обращенной к границе потока. Поэтому первая составляющая силы Жуковского при любых условиях пытается сместить частицу от границ
419
|
|
|
Рис. 8.12. Механизм возникновения первой составляющей силы Жуковского при наличии градиента скорости по сечению потока |
К центру потока, что способствует предупреждению пробкообразования. Первая составляющая силы Жуковского
= рГ щй, (8.13)
Где р — плотность жидкости; ui — скорость потока в сечении координаты центра тяжести частицы; d — диаметр частицы.
Циркуляция по контуру гравийной частицы из-за наличия градиента скорости по сечению потока
Г = | uidx. (8.14)
І
Для сферичной формы частиц после интегрирования равенства (8.14) и подстановки результата в уравнение (8.13) получим уравнение дли определения величины первой составляющей силы Жуковского
FX1 =wS(щ2 - u22), (8.15)
Где у — коэффициент сопротивления; S — площадь Миделевого сечения частицы; u1, u2 — скорости обтекания частицы по противоположным относительно оси симметрии потока сторонам.
Величину скорости в любой точке сечения потока легко определить, если известен закон ее распределения по сечению потока. Большинство авторов утверждают, что при ламинарном режиме этот закон с достаточной точностью (для практических расчетов) может быть выражен параболой вида u = ax2 + b. Принимая во внимание справедливые для ламинарного режима движения сме-
420
Си граничные условия о равенстве максимальной удвоенной средней скорости потока umax = 2U и учитывая, что на стенках скважины и труб X = ±(D0 - Аф)/2 скорость потока U равна нулю, получаем уравнения для определения скоростей обтекания частицы по противоположным от вертикальной оси симметрии сторонам
|
D X — 2 |
|
U1 = 2u |
(Ак - Аъ)
И
D
X + — 2
(Dк - Аф)
Диаметр обсадной и фильтровой колонны соответст-
Где Ак, Аф венно.
|
U, = 2u |
|
1 -■ |
Выражая среднюю скорость потока u через расход смеси Q и площадь сечения потока ®кп = 0,785(Ак : Аф) и подставляя значения u и u2 в уравнение (8.15), получаем выражение для первой составляющей силы Жуковского
|
= 4Wd 2Q2 |
|
4(x - 0,5d)2 A S 2 |
|
4(x + 0,5d)2 A S 2 |
|
^Ж1 = |
|
1 - |
|
1 - |
|
(8.16) |
|
(Ак - Аф)2 |
Где A S — размер кольцевого зазора (A S = Ак — Аф).
Первая составляющая силы Жуковского способствует смещению частиц из периферийных в центральные сечения потока, препятствуя тем самым формированию первичных структур гравийных пробок по второму варианту пробкообразования.
Из уравнения (8.16) следует, что первая составляющая силы Жуковского достигает своих максимальных значений у стенок потока (градиент скорости максимален) и минимальных значений — в центре потока (скорость обтекания частицы по противоположным поверхностям одинакова и сила Жуковского для сферичной частицы обращается в нуль). Очевидно, что выражение (8.16) справедливо для восходящего и нисходящего ламинарного потоков. С целью объяснения механизма перемещения частиц из центральных сечений к границам потока и их зависания на стенках скважины и труб, способствующего пробкообра - зованию, были проанализированы возможные причины и сферы проявления такого смещения. На частицу действует горизонтальная составляющая силы гидродинамического давления Fгд.
421
Характер возникновения этой силы становится понятен, если представить действие ламинарного потока на поверхность частицы как действие бесконечного числа параллельных струек жидкости бесконечно малого диаметра на наклонную плоскость, что справедливо согласно определению ламинарного режима движения потока.
|
|
|
U=f(x, j) Grad И>0 |
|
Рис. 8.13. Механизм возникновения горизонтальной составляющей силы гидродинамического давления при наличии градиента скорости по сечению потока |
|
422 |
Горизонтальная проекция гидродинамического давления состоит из двух составляющих (рис. 8.13). Первая составляющая, действующая на четверть поверхности сферы и находящаяся ближе к оси симметрии потока, отлична от второй, действующей на четверть поверхности сферы, близлежащей к границе потока. В результате различия (по величине) первой и второй составляющих гидродинамического давления возникает усилие, действующее на частицу в горизонтальной плоскости. В восходящем потоке сила гидродинамического давления пытается сместить частицу от центра к границам потока, так как горизонтальная составляющая Fra, действующая на четверть поверхности частицы, обращенную к оси потока, выше, чем на противоположную поверхность. В нисходящем потоке действующую на частицу силу правильнее назвать не силой гидродинамического давления, а силой гидродинамического сопротивления. Скорость движения частицы в нисходящем потоке выше, чем скорость движения жидкости. Скорость жидкости в любом сечении нисходящего ламинарного потока увеличивается от границ к центральным сечениям, а скорость движения частиц не зависит от ее положения
|
|
|
B |
|
(8.17) |
В потоке. Поэтому можно утверждать, что абсолютная скорость частицы относительно слоев жидкости тем больше, чем меньше эта частица удалена от оси потока. Следовательно, для нисходящего потока горизонтальную составляющую силы гидродинамического сопротивления можно также определить через действие элементарных струек на поверхность частицы (см. рис. 8.13). Действие элементарной струйки на частицу в горизонтальной плоскости определяется выражением
/гд = 0,5р u2S sin 25,
Где u — скорость элементарной струйки жидкости; 5 — угол наклона касательной к поверхности частицы и вертикали.
Проинтегрировав уравнение (8.17) с учетом градиента скорости по поверхности частицы, получим уравнение для определения горизонтальной составляющей гидродинамического давления (сопротивления)
|
|
|
|
В восходящем потоке первая составляющая силы Жуковского способствует смещению частиц от границ к центру, а горизонтальная составляющая гидродинамического давления наоборот, препятствует такому смещению. Первая составляющая силы Жуковского в п/2 превышает горизонтальную составляющую силы гидродинамического давления, поэтому в установившемся режиме сферичные частицы движутся всегда в центральных сечениях потока и первичные структуры гравийных пробок по второму варианту пробкообразования (см. рис. 8.11, г, д, е) не образуются.
В нисходящем потоке первая составляющая силы Жуковского и горизонтальная составляющая гидродинамического сопротивления способствуют смещению частиц из периферийных в центральные сечения потока и первичные структуры гравийных пробок по второму варианту также не формируются. Эпюра распределения усилия, смещающего сферичную частицу к центру в зависимости от положения частицы в потоке, представлена на рис. 8.14. Очевидно, что чем дальше частица находится от центра потока и чем больше ее диаметр, тем выше действующее на нее суммарное усилие.
423
|
Рис. 8.14. Эпюры распределения усилия, действующего на сферичную частицу различной крупности по сечению потока и смещающего ее к центру |
Вывод о том, что сферичная частица всегда движется в центре вертикального потока [см. уравнения (8.16) и (8.18)] хорошо согласуется с экспериментальными данными А. Е. Смолдырева, проводившего скоростную киносъемку движения сферичных шариков в вертикальном потоке. Итак, при закачке в скважину частиц сферичной формы (согласно второму варианту) пробкообразования наблюдаться не будет.
На практике обеспечить снабжение гравием только идеально сферичной формы невозможно. Известны классификации гравийных частиц по форме. Типичные формы гравийных частиц определяются коэффициентами окатанности и сферичности (рис. 8.15).
При движении частицы неправильной формы возникает сложное обтекание жидкости по контуру частицы, определяющееся не наличием градиента скорости по сечению потока (первая составляющая силы Жуковского), а формой частицы. Циркуляция жидкости по контуру гравийной частицы, вызванная ее неправильной формой, приводит к возникновению дополнитель - 424
|
|
|
0,9
0,3 |
OGG <3 G О
|
(8.19) |
Рис. 8.15. Типовые формы частиц
Ного усилия, действующего на частицу в горизонтальной плоскости, которое было названо второй составляющей силы Жуковского. Вторая составляющая силы Жуковского может быть определена из выражения
РЖ2 =Р Щ $ rot uidS.
Форма гравийных частиц (см. рис. 8.15) при обтекании жидкостью хорошо описывается тремя параметрами: большим d и малым d' радиусами обтекания частицы и длиной вытянутой части частицы /'. Из энергетической теории гидротранспорта следует, что частица гравия в потоке движется как и жидкость в водоносном пласте — по пути наименьшего сопротивления. Для гравийной частицы это означает, что в процессе транспортировки она ориентируется в потоке таким образом, чтобы сопротивление обтеканию было минимальным. Если принять во внимание, что сила сопротивления пропорциональна площади сечения частицы, перпендикулярного направлению потока, то можно предположить, что частица располагается вытянутой стороной вдоль оси потока и поэтому на циркуляцию жидкости вдоль контура частицы влияет только большой и малый радиус обтекания. Обозначим отношение d'/d коэффициентом формы гравийных частиц K. Решая уравнение (8.19) с учетом принятого коэффициента формы гравийных частиц, получаем выражение для определения второй составляющей силы Жуковского
425
=Ті <■ - k> І'-A • <8^20)
Вторая составляющая силы Жуковского способствует смещению частицы к границам потока. С учетом влияния формы на горизонтальное перемещение частиц в потоке дифференциальное уравнение движения частицы (8.12) при установившемся режиме запишется в следующем виде:
Для случая засыпки в восходящем потоке жидкости
—(mvx) = 2,35 „ [7,08(1 - K)| 1 -
|
±[pV Sv2x dvx ); (8.21) |
Dt (D2 - £>Ф)[4] I AS2
■ 1 4( x + 0,5d)2 Y І1 4( x - 0,5Kd)2^2 AS2 J V AS2
Для случая засыпки в нисходящем потоке жидкости
D(mVX) = 10,[5]2[6]^і2 [1,57(1 - K)(1 - ixl) - Dty x/ D - D|)2 V aS2 J
|
4(x - 0,5Kd)2 2 A S |
|
4( x + 0,5d )2 2 A S |
|
±[py Svx2 +ЦФ dvx ), (8.22) |
|
-11 - |
|
-11 - |
Где ц — вязкость жидкости.
Выражения (8.21) и (8.22) представляют собой нелинейные дифференциальные уравнения второго порядка, которые не решаются обычными методами интегрирования. При анализе условий формирования первичных структур гравийных пробок за счет смещения частиц из центральных в периферийные сечения потока первостепенное значение приобретает оценка установившегося движения частиц, для которого справедливы граничные условия
предупреждения зависания частиц гравия в процессе закачки большой интерес представляет нахождение таких значений К, при которых частица будет прижиматься к границам потока. Приравняем к нулю правые части уравнений (8.21) и (8.22), подставим значения х, характерные для границ потока [х = ±0,5х х(Ок — - Оф)] и предположив, что размер частицы гравия значительно меньше размеров кольцевого пространства, получим, что при закачке в восходящем потоке воды, критический коэффициент формы Ккр, при котором частица начинает прижиматься к границам потока, равен 0,76. При закачке гравия в нисходящем потоке Ккр = 0,32. Распределение частиц гравия в процессе закачки для восходящего и нисходящего потоков в зависимости от коэффициента формы частиц представлено графиками на рис. 8.16. В качестве геометрического критерия подобия потока автором при построении графиков принималась безразмерная величина j = 2х/(Ок — Оф), которая на границах потока принимает значения ± 1, а в центре равна нулю.
|
|
|
-1 |
|
Рис. 8.16. Распределение частиц гравия в поперечном сечении восходящего (1) и нисходящего (2) потоков |
|
|
|
Рис. 8.17. Вращение частицы в потоке |
|
427 |
Из представленных графиков видно, что при закачке в нисходящем потоке жидкости требования к качеству материала с учетом исключения возможного зависания могут быть менее строгими, чем для восходящего потока. При засыпке гравия в нисходящем потоке пригоден материал, коэффициент формы частиц которого больше 0,32, а в восходящем потоке необходимо использовать гравий более правильной формы (К > 0,76).
За счет наличия градиента скоростей жидкости по сечению потока в некоторых случаях будет наблюдаться вращательное движение частиц гравия. В связи с этим целесообразно оценить влияние возможного вращения на перемещения частиц в горизонтальной плоскости.
|
(8.23) |
На рис. 8.17 показана гравийная частица в вертикальном потоке жидкости. Очевидно, что вращение частицы в некоторой точке сечения потока будет наблюдаться, если вращательный момент, стремящийся повернуть частицу по часовой стрелке M2, больше вращательного момента, поворачивающего частицу против часовой стрелки М1. Величина вращательных моментов определяется величиной гидродинамического давления (сопротивления) на противоположные от центра тяжести поверхности частицы
DM12 = dEia dS.
Проинтегрировав выражение (8.23) по поверхности гравийной частицы, получим уравнения для моментов
|
1 - |
|
4X A? 2 |
|
-11 - |
|
-11- |
|
(8.24) |
M1 = 3,24a d +1' Sin p
4 x
1-
A S
4(x - 0,5D)[7]
|
4(x + 0,5/ sin p)2 AS2 |
|
1- |
M 2 = 3,24a (1 - sin p) (d -1' sin p)
|
4(x + 0,5D )2 2 A S |
|
4( x + 0,5D +1' sin p)2 2 A S |
|
-11 - |
|
+d(1 - cos P) |
|
1- |
4(x + 0,5D +1' sin p + 0,5D sin p)
2
|
Y'pSQ l' sin p (D2-D!) ' |
|
+ 1 1- |
|
+ 3,24 |
A S
4(X + 0,5D + L' sin p)2
2
|
4(X + 0,5D )2 2 A S |
|
-I 1 - |
|
(8.25) |
|
1 - |
A S
Где у' — коэффициент обтекания цилиндрической части гравийной частицы, изменяющейся в зависимости от величины угла от 0,11 до 0,2. '
Сравнивая значения Mi и М2, полученные при расчетах по
428
Формулам (8.24) и (8.25), можно судить о характере вращательного движения частицы данной формы. Если М1 больше M2 при любых значениях угла наклона частицы к вертикали р для определенной точки потока, то в этой точке частица будет вращаться. В противном случае, при определенном значении р моменты Mi и М2 уравновешиваются и частица движется при установившемся наклоне к вертикали без вращения. Графики изменения угла стабильного движения частиц различной формулы Кп = = l'/d no сечению потока представлены на рис. 8.18. Если угол наклона большей оси симметрии частицы к вертикали превышает 90°, то частица в этом сечении потока будет вращаться. Вращение частиц наблюдается преимущественно в периферийных областях потока, где велик градиент скорости. При смещении частиц к центру вращение постепенно затухает. Частицы с коэффициентом продолговатости Кп = 0,25 вращаются только в области от границ потока j = ±1 до значений j = ± 0,4. Сферичные частицы вращаются по всему сечению потока за исключением центра.
В потоке вращаются только скатанные частицы с коэффициентом продолговатости Кп < 0,5 (см. рис. 8.17). С увеличением продолговатости частиц область вращения частиц в потоке сужается от центральных к периферийным сечениям и уменьшается угол наклона частиц к оси потока частиц, двигающихся без вращения. Проанализировав выражения (8.21), (8.22), (8.24) и (8.25), было получено, что за счет горизонтального усилия, действующего на частицу, определяемого из уравнений (8.21) и
|
|
|
Рис. 8.18. Изменение угла наклона частицы по сечению потока от ее формы |
|
429 |
|
-1 |
|
О |
|
И |
(8.22), частица определенной формы Кп будет стремиться занять в потоке строго определенное положение (см. рис. 8.16), в котором гидродинамическое давление на противоположные от центра тяжести поверхности частицы равны, и соответственно равны моменты M1 и М2. При достижении частицей точки сечения потока, в которой М1 уравновешивает М2, частица гравия продолжает двигаться в этом слое жидкости в строго вертикальном положении без вращения.
В соответствии с этим, при засыпке гравия наблюдается вращение окатанных частиц (Кп < 0,5) в потоке. Однако период вращения частиц очень незначителен, так как под действием горизонтальных сил частица смещается в такое сечение потока, в котором значении M1 и M2 уравновешивают друг друга и учитывать влияние вращения частиц в потоке на горизонтальное перемещение частицы гравия нецелесообразно.
В ламинарном потоке жидкости создаются благоприятные условия для образования гравийных пробок в случае, если при засыпке используют гравий неправильной формы, характеризующийся значениями меньшими критических. С увеличением концентрации частиц гравия критической формы в потоке вероятность пробкообразования увеличивается, но оценить это влияние возможно только экспериментальным путем. Вывод о влиянии формы на распределение частиц по сечению потока в горизонтальной плоскости подтверждается экспериментальными данными, полученными различными исследователями. Однако ранее это явление не имело научного обоснования. Смещение частиц гравия к границам потока, их налипание и скопление на стенках скважины и обсадных труб есть необходимое, но не достаточное условие пробкообразования. Доставку гравия в зону фильтра можно обеспечить, если первичные структуры гравийных пробок, образующихся в потоке, не сохраняют свою устойчивость и под влиянием многих факторов разрушаются.
Возможность образования устойчивого контура равновесия в сыпучих породах при креплении горных выработок была рассмотрена М. М. Протодьяконовым. Применение предложенной методики не позволяет оценить устойчивость гравийной пробки в кольцевом пространстве скважины, так как в значительной степени она определяется характером фильтрации жидкости в гравийном материале.
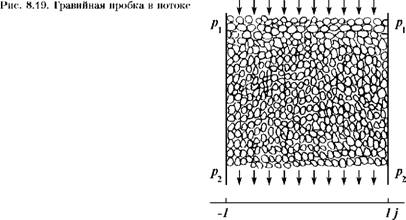
Оценим устойчивость гравийной пробки к разрушению в ламинарном потоке жидкости. При малых скоростях движения потока фильтрация жидкости через гравийную пробку (рис. 8.19) подчиняется закону Дарси. Потери напора на гравийной пробке за счет наличия фильтрации 430
|
|
H = - QL_, (8.26)
Кф WKn
Где L — высота пробки; Кф — коэффициент фильтрации пробки; wKn — площадь поперечного сечения пробки.
С учетом уравнения Бернулли, записанного для верхнего и нижнего сечений гравийной пробки, перепад давления определится из выражения
Ap = p - Р2 = PGLF- il. (8.27)
^ Кф ^кп )
Закон сопротивления при обтекании тел жидкостью в общем виде
Fc = +у'р d 2»ф. (8.28)
Если силы инерции и вязкости малы (при ламинарном потоке в скважине), то второй член выражения (8.28) приближенно равен нулю и им можно пренебречь. В связи с эти запишем, что сила сопротивления при фильтрации прямо пропорциональна скорости потока или квадрату координаты, т. е.
Fc □ j2. (8.29)
С учетом уравнения (8.29) можно записать, что закон распределения гидродинамического давления потока на пробку по сечению потока в общем виде
431
Ргд = Pmax (1 - j2), (8.30)
Где pmax — максимальное гидродинамическое давление по сечению пробки.
Площадь эпюры под кривой распределения гидродинамического давления по сечению потока равна силе гидродинамического давления на гравийную пробку. Интегрируя уравнение (8.30), получаем выражение для определения силы гидродинамического давления в координатах при фильтрации жидкости через пробку
РГд = 3 Pmax. (8.31)
Сила гидродинамического давления на пробку равна произведению средней величины давления потока на площадь потока, В координатах Ргд = f (J) справедливо равенство
РГд = 2 p. (8.32)
Решая совместно уравнения (8.31) и (8.32), получаем
Pmax = 3 Р. (8.33)
Закон распределения гидродинамического давления на пробку по сечению потока с учетом выражений (8.30) и (8.27) примет вид
РГд = 3РGLМ--------------- 1І(1 - j2). (8.34)
Д 2 I Кф ®кп )
Кроме гидродинамического давления на свод гравийной пробки действует статическое усилие, равное весу вышележащих гравийных частиц
Рс =р gL е (Рї - 1І, (8.35)
Где рп — плотность породы; е — пористость породы.
Общее давление на своде пробки равно сумме гидродинамической и статической составляющих
|
(8.36) |
|
Р = РГд + РС = Р GL |
Рї - 1| e + 3 f-^- - 1 1(1 - j2)
2 1 Кф ®кп
432
Рассмотрим возможность образования устойчивого свода гравийной пробки в ламинарном потоке при заданной величине действующей нагрузки, определяемой из уравнения (8.36).
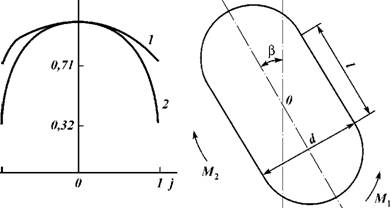
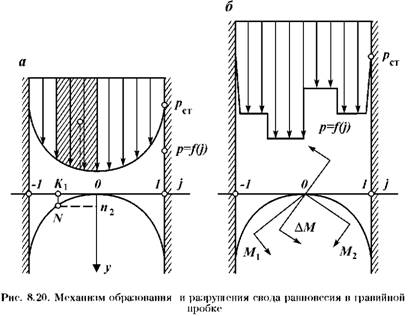
Контур гравийной пробки будет устойчив к разрушению, если моменты активных сил, действующих на свод гравийной пробки относительно некоторой точки N с координатами n1 и n2, принадлежащей этому контуру, равны. Образование устойчивого свода равновесия гравийной пробки в кольцевом пространстве скважины при ламинарном режиме движения потока и действующая на этот контур нагрузка показаны на рис. 8.20, а, б.
Момент, стремящийся сдвинуть свод равновесия по часовой стрелке,
M2 = N1n1. (8.37)
Интегрируя уравнение (8.37) от нуля до Пі, по dj, получаем
P + 3- OPGL (j2 - NL)
|
M2 = 0,5n2 |
|
(8.38) |
2 ^ Кф ®кп )
Момент, стремящийся сдвинуть свод равновесия по часовой
|
433 |
Стрелке, равен произведению реакции правой части свода на координату
M1 = N2n2. (8.39)
Реакция правой части свода равновесии N2 равна произведению суммарного усилия активных сил на правую часть свода на коэффициент бокового распора
M, = 0,5Р®^2 (1^j П2, (8.40)
Где 6 — угол внутреннего трения.
Площадь кольцевого пространства скважины в системе координат j равна двум и выражение (8.40) запишем в следующем виде:
2 (90 - 6
M, = Р tg2 ——) щ. (8.41)
Согласно условию равновесия свода гравийной пробки М2 = = Мі. Решая совместно уравнения (8.38) и (8.41) и принимая, что коэффициент бокового распора равен 0,5, получаем уравнение свода равновесия
1 (j 2 - x2 )
|
(8.42) |
|
У = x |
Р
В начальный период образования пробки ее высота незначительна и статической составляющей нагрузки на свод пробки можно пренебречь. В этом случае уравнение (8.42) запишется в более простом виде
Y = x2(2 - x2). (8.43)
Из выражений (8.42) и (8.43) следует, что при ламинарном режиме движения потока в кольцевом пространстве скважины гравийные пробки, сформировавшиеся за счет налипания, зависания частиц гравия неправильной формы на стенках скважины и обсадных труб сохраняют устойчивое состояние и препятствуют надежной доставке гравия в зону фильтра. Свод гравийной пробки в ламинарном потоке жидкости принимает вид параболы, причем с увеличением высоты гравийной пробки (возрастает статическая составляющая нагрузки на пробку) ветви параболы занимают более крутое положение, что свидетельствует о повышении устойчивости гравийной пробки к разрушению. 434
Пробкообразование в турбулентном потоке жидкости
Сложность оценки перемещения частиц в турбулентном потоке связана с отсутствием количественного описания турбулентности. Из многочисленных работ, посвященных этой проблеме, целесообразно выделить и взять за основу последующих исследований работу X. Шуберта, Т. Нессе и П. Коха, в которой предложена оригинальная качественная теория переноса частиц в турбулентном потоке. Турбулентный поток представлен как некоторое постоянно изменяющееся поле вихревых скоростей, наложенное на поле осредненных скоростей. В этой связи турбулентный перенос частиц в потоке определяется с одной стороны вихревым полем изменяющихся скоростей, а с другой — полем осредненных скоростей
Qi = - Dt^ - vxnt, (8.44)
Dx
Где QI — показатель турбулентного переноса i-ой частицы гравия; Dt — коэффициент диффузии; Ni — число частиц гравия, проходящих через некоторую вертикальную плоскость.
Первый член уравнения (8.44) определяет количество частиц, проходящих через некоторую вертикальную плоскость в потоке гравийной смеси за счет турбулентной диффузии. Горизонтальное перемещение частиц в потоке под действием вихревого поля скоростей определяется коэффициентом диффузии Dt, значения которого находятся только опытным путем. Очевидно, что такой подход к оценке перемещений частиц в потоке может объяснить экспериментальный материал, но не позволяет оценить условия прижатия частиц к стенкам скважины и обсадных труб и выявить определяющие его факторы.
Рассмотрим влияние вихревого поля скоростей потока на горизонтальное перемещение частиц. Согласно теореме Жуковского, подъемная сила, возникающая вследствие циркуляции вихрей и перпендикулярная к оси потока, который движется в бесконечности с некоторой скоростью, равна плотности жидкости, умноженной на циркуляцию, скорость потока и длину обтекаемого тела. Теорема Жуковского применима для определения подъемной силы любых тел, движущихся в жидкости. Н. Е. Жуковский разработал теорию присоединения вихрей, основная идея которой заключается в том, что обтекаемые тела могут быть заменены вихрями. Поэтому можно воспользоваться теоремой Жуковского применительно к движению самих вихрей. На любой вихрь, когда он перемещается внутри жидкости, всегда действует сила, направленная так же, как и сила Жуковского, т. е.
435
Нормально к оси обтекающего вихрь потока. Под действием этой силы вихри будут смещаться в направлении, где скорость больше, т. е. от периферии к оси потока.
Вихрь, двигаясь в направлении, перпендикулярном к оси потока, подвергается также действию сил трения и поэтому его путь не будет прямой линией, а будет изогнут в виде дуги, обращенной своей выпуклостью навстречу потоку. Кроме того, вихри создают определенное поле скоростей в жидкостях. Поскольку вихри образуются в слоях с малыми скоростями, они будут тормозить движение этих слоев и, следовательно, уменьшать их скорость. Итак, вихри будут выравнивать скорости в поперечном сечении потока, что имеет большое значение для процессов массообмена и распределения гравийных частиц в поперечном сечении потока.
Определим соотношение между подъемной силой вихря и силой сопротивления Fc, испытываемой им при перемещении в жидкости. Заменяя циркуляцию скорости в уравнении (8.13) работой силы на поверхности вихря поперечного сечения Sn, получаем
_ 2
Fв = Сп р (8.45)
Где Fjj - подъемная сила вихря; Сп — коэффициент подъемной силы, определяемый опытным путем; _ - осредненная скорость турбулентного потока.
При перемещении вихря необходимо преодолеть силу сопротивления, которая определяется по формуле
—2
_в
Fc = C0P , (8.46)
2
Где С0 — коэффициент сопротивления, зависящий от числа Рей - нольдса; _в — скорость подъема турбулентного вихря.
Приравнивая силы Fв и Fc, получаем скорость подъема вихря
_в = pL _. (8.47)
V С0
Судя по опытам Прандтля, величины Сп и С0 имеют один порядок и поэтому можно полагать, что скорость вихря _в будет соизмерима со скоростью потока _.
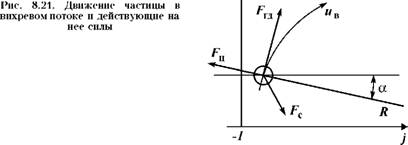
Рассмотрим движение частиц гравия в единичном вихре, перемещающемся согласно теореме Жуковского о подъемной силе от периферии к оси симметрии потока по дугообразной траектории (рис. 8.21). В горизонтальной плоскости перемещение частиц 436
|
|
Под действием единичного вихря определяет соотношение трех сил: горизонтальной составляющей центробежной F4, гидродинамического давления Fm и сопротивления FQ. Дифференциальное уравнение движения гравийной частицы в потоке запишем в виде
D 2 x i=n
M— = Z FX = - F, + Fгд ± Fc. (8.48)
Dt i=1
Центробежная сила Fц, действующая на гравийную частицу, определяется массой частицы т, скоростью движения частицы V И радиусом закручивания вихря R. Как отмечалось выше, скорость движения частиц в турбулентном потоке приравнивается к скорости движения самого потока вследствие малости относительных скоростей движения жидкости и частиц в сравнении со скоростью потока. Поэтому при оценке величины центробежной силы удобнее пользоваться не скоростью частицы v, а скоростью потока U. Вихри зарождаются у границ потока, а затем закручиваются к его центру, в связи с чем радиус закручивания вихря можно приравнять к радиусу потока гравийной смеси. Если учесть принятые обозначения, то величина центробежной силы
П mv2 пd3p„ — 2 /0 in
F,, =------ =------ ^ w2 cos а, (8.49)
Ц R 3AS v У
Где а — угол наклона вихря к оси потока.
Горизонтальная составляющая гидродинамического давления определится по аналогии с уравнением (8.17)
_ —2
FТд =wSu-sin а. (8.50)
Очевидно, что центробежная сила способствует смещению частиц к периферии потока, а сила гидродинамического давления вихря — наоборот — к его центру. Сила сопротивления Fc имеет
437
Направление, противоположное направлению движения частицы, и не может самостоятельно вызывать горизонтальное перемещение частиц в потоке, так как определяет только скорость и время движения частиц, не изменяя его направления. В этой связи, тенденцию перемещения частиц в горизонтальной плоскости определяют только первые две составляющие дифференциального уравнения (8.48), а сила сопротивления считается их производной. Из выражений (8.49) и (8.50) следует, что центробежная сила пропорциональна диаметру частицы гравия в кубе, а сила гидродинамического давления — квадрату диаметра частицы. С увеличением размеров частиц центробежная сила возрастает быстрее, чем сила гидродинамического давления, и при определенном диаметре частиц будет наблюдаться смещение частиц к границам потока и их зависание на стенках скважины и обсадных труб, что приводит к образованию гравийной пробки. Приравнивая правые части уравнений (8.49) и (8.50), получаем выражение для определения критического диаметра частиц гравия, выше которого под действием единичного вихря частицы налипают, зависают на границах потока
D^ = 0,375уД5 tg а. (8.51)
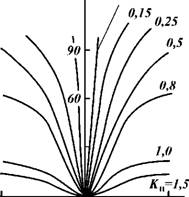
Угол наклона вектора скорости вихря к вертикали а определяется соотношением вертикальной и горизонтальной составляющих скоростей вихря. Как показали исследования, в зависимости от числа Рейнольдса горизонтальная проекция вектора скорости вихря может достигать трех десятых вертикальной скорости вихря йв или в соответствии с уравнением (8.47) трех десятых средней скорости потока U. При незначительной степени турбулизации потока, что наблюдается при переходе от ламинарного к турбулентному потоку (Re = 1200), горизонтальная составляющая проекции скорости вихря равна приблизительно десятой части средней скорости потока. В этой связи угол а — функция числа Рейнольдса, в зависимости от степени турбулизации потока — изменяется от 6 до 16°.
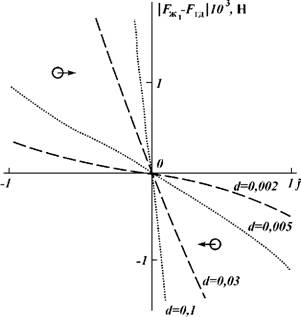
На рис. 8.22 представлена зависимость критического диаметра гравийных частиц, при котором наблюдается пробкообразование, от числа Рейнольдса для различных сечений кольцевого пространства скважины F. При зазоре между стенками скважины (обсадных труб) в 100 мм при незначительной турбулизации потока (Re = 1200) частицы размером более 0,6 мм зависают на границах потока. С ростом степени турбулизации потока критический диаметр зависших частиц увеличивается и достигает при развитой турбулентности (Re = 6400) 1,7 мм, что свиде - 438
|
Re 6400 |
|
|
|
1200 |
Рис. 8.22. Зависимость критического диаметра частиц гравия, смещающихся к границам потока в турбулентном потоке, от числа Рейнольдса при разных значени-
Ях f.
1 - 0,1; 2 - 0,15; 3 - 0,2
1 2 3d, 10 і М
Тельствует об уменьшении вероятности пробкообразования с ростом числа Рейнольдса. Из формулы (8.51) следует, что при увеличении межтрубного зазора в скважине Д5 критический диаметр частиц также возрастет. Если учесть, что размер гравийных частиц, засыпаемых в скважину, редко превышает 2—3 мм, то согласно уравнению (8.51) при кольцевом зазоре Д5 > 0,5 м налипания частиц на границы потока под влиянием вихрей можно избежать.
|
0 |
Горизонтальное перемещение в турбулентном потоке определяется не только влиянием вихревого поля скоростей, но и поля осредненных скоростей потока [см. формулу (8.44)]. Дифференциальное уравнение движения частиц в горизонтальной плоскости под действием поля осредненных скоростей потока соответствует выражению (8.22). Отметим, что при турбулентном потоке частицы распределяются по сечению в зависимости от их формы, однако характер этого распределения будет отличен от распределения в ламинарном потоке. Отличие заключается в различных изменениях осредненных скоростей потока по его сечению и градиенте скорости, который согласно формулам (8.15), (8.18) и (8.20) определяет горизонтальное перемещение частиц в потоке.
Характер изменения осредненных скоростей турбулентного потока описывается следующим уравнением:
|
|
(8.52)
Где u - скорость турбулентного потока в сечении, соответствующем центру тяжести i-ой частицы.
Решая дифференциальное уравнение (8.22) с учетом равенства (8.52), получим кривые распределения частиц по сечению турбулентного потока в зависимости от их формы (см. рис. 8.16). Коэффициент критической формы Ккр для турбулентного потока соответствует критическому коэффициенту формы для ламинарного потока и равен для восходящего направления движения
439
Гравийной смеси 0,76, а для нисходящего — 0,31. При коэффициенте формы, меньшем критического, гравийная частица под действием осредненного поля скоростей стремится зависнуть, налипнуть на границы потока, что способствует пробкообразованию.
При турбулентном потоке (в отличие от ламинарного) влияние формы частиц наблюдается только для определенных сечений вертикального потока, которые принято называть в технической литературе пограничным слоем. В ядре потока частицы различной формы распределены равномерно и движутся хаотично, подчиняясь законам диффузии. В пограничном слое влияние формы частиц на их горизонтальное перемещение особенно велико, что качественно отличает этот слой от ядра потока.
Распределение гравийных частиц по поперечному сечению турбулентного потока в зависимости от коэффициента критической формы будет искажаться за счет воздействия вихревого поля скоростей. Однако вихревое воздействие носит временный характер и за счет наличия градиента осредненной скорости по сечению потока будет наблюдаться смещение частицы в зависимости от ее формы либо к границам, либо к ядру потока.
В турбулентном потоке могут возникнуть условия, способствующие смещению частиц к периферии потока и их зависанию на стенках скважины и обсадных труб (см. рис. 8.16-8.22). Вероятность пробкообразования в турбулентном потоке увеличивается с ростом размеров гравийных частиц и уменьшении коэффициента их формы. Поэтому в первую очередь налипнуть на стенки скважины и обсадных труб должны частицы неправильной формы наиболее крупной фракции гравия, используемого при засыпке. Увеличение степени турбулизации, а также площади сечения потока гравийной смеси позволяет уменьшить вероятность пробкообразования, но не устраняет его, так как для исключения возможного зависания частиц кольцевой зазор скважины должен более 0,5 м, что не соответствует установленным требованиям к конструкциям скважин.
В связи с тем, что турбулентный режим движения гравийной смеси не устраняет (в большинстве случаев) горизонтального смещения частиц от центра к периферии потока, их налипания на стенки скважины, особую важность приобретает вопрос оценки устойчивости образующихся первичных структур гравийной пробки к разрушению в турбулентном потоке. Предположим, что за счет смещения гравийных частиц к периферии потока образовалась гравийная пробка. Тогда на каждую точку устойчивого свода равновесия действуют моменты М1 и М2 от статической и гидродинамической нагрузки, уравновешивающие друг друга (см. рис. 8.20, б). ' ' ' '
440
|
(8.53) |
|
(8.54) |
|
(8.57) |
|
441 |
Известно, что турбулентный поток характеризуется наличием пульсирующей продольной составляющей скорости потока, т. е. на некотором интервале потока, равном размеру вихря, мгновенные скорости увеличиваются, но согласно условию постоянства расхода жидкости в процессе закачки гравия, на противоположном от центра потока интервале мгновенная скорость вихря уменьшается на такую же величину (при равенстве площадей сечения, возросшего и уменьшающегося по скорости вихря). За счет мгновенного изменения скоростей потока относительно центра симметрии свода возникает дополнительный момент ДМ, стремящийся провернуть свод образовавшейся пробки. Согласно гипотезе М. М. Протодьяконова устойчивый контур равновесия в сыпучих породах будет разрушаться при выполнении условия
Д M > M1
В начальный период образования гравийной пробки статической нагрузкой, действующей на свод пробки от веса вышележащих гравийных частиц, можно пренебречь. Тогда из уравнения моментов для центра симметрии свода равновесия получим величину отношения приращения гидродинамической нагрузки ДРгд за счет мгновенного изменения скоростей потока к гидродинамической нагрузке Fra от поля осредненных скоростей потока, при котором гравийная пробка в турбулентном потоке будет разрушаться, т. е. справедливо выражение
^ > 0,25^-.
Приняв, что мощность турбулентного вихря в 4 раза меньше сечения потока, что наблюдается при развитом турбулентном режиме, преобразуем выражение (8.54)
|
|
(8.55)
Сила гидродинамического давления на свод пробки пропорциональна квадрату скорости потока и поэтому справедливо следующее соотношение
|
|
(8.56)
Или
ДИ > 1,41и, ДИ = ив - и.
Из выражения (8.57) следует, что структура гравийной пробки, при принятом (согласно М. М. Протодьяконову) запасе устойчивости, будет всегда разрушаться, если мгновенная скорость потока превышает осредненную скорость в 1,41 раза. Известно, что при развитом турбулентном режиме движения потока мгновенные скорости могут в два и даже более раз превышать средние. Следовательно, в начальный период образования пробка будет всегда разрушаться.
При увеличении высоты гравийной пробки, образовавшейся в кольцевом пространстве скважины, статическая составляющая нагрузки от веса вышележащих гравийных частиц на свод равновесия растет и соответственно снижается роль дополнительной составляющей гидродинамической нагрузки, возникающей за счет наличия пульсации скоростей потока. При определенной высоте гравийной пробки она не будет подвержена разрушению в турбулентном потоке. Для определения критической высоты гравийной пробки, при которой она сохраняет свою устойчивость, запишем выражение (8.55) с учетом статической нагрузки Fct
A F
Гд > 0,5. (8.58)
Учитывая, что мгновенные скорости турбулентного потока могут примерно в 2 раза превышать средние и величина AFra согласно уравнению (8.50) будет достигать значений, в 4 раза превышающих Fm, получим критическое соотношение между статической и гидродинамической нагрузками на свод равновесия гравийной пробки
Fct = 7Fra. (8.59)
Подставляя в выражение (8.36) значения Fct и Fm, определенные выше, и решая уравнение относительно критической длины гравийной пробки, при которой она не подвержена разрушению в турбулентном потоке, получаем
L кр =--------- ^------------- , (8.60)
Кр пG(P„ /Р - 1)(1 - е)' v у
Где е — пористость гравийной пробки.
При увеличении высоты пробки выше LTO ее устойчивость в соответствии с формулой (8.60) будет расти и работы по ликвидации пробкообразования в кольцевом пространстве скважины осложнятся.
442