Прогрессивные технологии сооружения скважин
КАРКАСЫ ФИЛЬТРА
В качестве каркасов фильтра используют разные конструкции, которые подробно описаны в работах В. С. Алексеева и других авторов. В мировой практике производства фильтров наметилась четкая тенденция замены многообразных конструкций на каркасы с проволочной обмоткой. Это относится только к условиям, когда продуктивный пласт сложен песками различного фракционного состава. В относительно устойчивых породах, ва - лунно-галечных отложениях нет смысла обматывать перфорированные каркасы проволокой или другим материалом.
Проволочные фильтры, одну из первых конструкций которых разработал Ф. С. Бояринцев в 1952 г., претерпели существенные изменения. Прежде всего это касается перехода с круглого сечения проволоки на фигурное. В случае круглого сечения проволочной обмотки поверхность образуемой щели, контактирующая с породой, имеет форму клина. При откачке щель заполняется породой и возникает расклинивающий эффект, способствующий интенсивному уплотнению породы, закупорке фильтра.
Закупорка щелей при наличии в пласте мелких фракций песка и шлама, неоднородности гравийной обсыпки, наличии в ней кольматантов происходит быстро, в первые секунды откачки. Мелкие фракции и кольматант цементируют поровое пространство между более крупными частицами, находящимися в контакте с поверхностью проволоки, многократно снижая тем самым эффективную скважность фильтрующей поверхности. При этом осложняется раскольматация прифильтровой зоны, что вызывает необходимость предъявления жестких требований к технологии вскрытия пласта, расширению, фракционированию и намыву гравия.
Фирмой «Джонсон» [Великобритания] было предложено профилировать проволоку перед намоткой на каркас. Сечение профилированной проволоки получали треугольным. При навивке проволоки на опорные стержни каркаса одна из вершин треугольника направляется внутрь фильтра перпендикулярно его продольной оси симметрии.
Поверхность фильтра, контактирующая с породой, получается гладкой, без впадин около щелей и выступов между ними. В процессе откачки такая поверхность щели не способствует цементации и уплотнению породы вблизи фильтрующей поверхности, а наоборот, стимулирует вынос частиц, меньших по размеру ширины щели, и очищение прифильтровой зоны от шлама, мелких фракций и кольматантов.
Гидравлическое сопротивление фильтров с профилированным сечением обмотки меньше, чем с круглым, не только из-за большей проницаемости контактной зоны фильтрующей оболочки с породой. При прохождении потока через щель, имеющую в поперечном сечении форму расходящегося внутрь каркаса насадка, струя в момент вхождения в щель сжимается. Максимальное сжатие струи наблюдается не у фильтрующей поверхности, а на расстоянии 1-2 мм от нее внутрь. В интервале потока, характеризующегося минимальным сечением, скорости струи максимальны. С увеличением скорости, согласно уравнению Бернулли, уменьшается статическая составляющая и по аналогии со струйными аппаратами возникает вакуум. Вакуум также возникает между фильтрующей поверхностью и сечением максимального сжатия струи. На величину вакуума влияет сопротивление фильтра из профилированной проволоки меньше, чем круглой, в контакте с водной средой.
Кроме фирмы «Джонсон» аналогичные фильтры выпускают и другие ведущие фирмы, такие как «Бейкер» [США], «Нагаока» [Япония]. Профилированная проволока прикрепляется к опорным стержням каркаса контактной сваркой, что обеспечивает сплошность щели и необходимую прочность и целостность конструкции.
Недостатком известных конструкций считается перпендикулярность оси симметрии щелей фильтра оси симметрии скважины и фильтровой колонны. Такое пространственное расположение отверстий рационально только в том случае, когда мы имеем дело с плоскопараллельным фильтрационным потоком в скважину и скорость притока в фильтр в любом сечении независимо от длины постоянна. На практике плоскопараллельная фильтрация, как и радиально-сферичная, не встречается.
Обычно характер фильтрации носит промежуточный характер между плоскопараллельным и радиально-сферичным потоком. Прямое доказательство этого - эпюра входных скоростей в фильтр. Максимальные скорости фильтрации наблюдаются в верхних сечениях фильтра и постепенно (не линейно) убывают по направлению к забою скважины. При плоскопараллельной фильтрации входная скорость по длине фильтра - постоянная величина, а при радиально-сферичной фильтрации работает только верхний участок фильтра высотой, соответствующей его радиусу (остальная часть фильтра не работает). В этой связи очевидно, что градиент фильтрационного потока в реальных скважинных условиях направлен не перпендикулярно оси скважины (и параллельно пласту) и не в направлении верхних отверстий фильтра, а занимает определенное промежуточное положение, зависящее от свойств пласта, его размеров, режимов эксплуатации и др.
При фильтрации потока через известный фильтр направление движения флюида не совпадает с направлением градиента фильтрации, который перпендикулярен линии постоянного давления в околоскважинной зоне. Поэтому известная конструкция фильтра выполняет функцию местного сопротивления, заставляющего поток при прохождении через фильтрующую оболочку временно изменять свое направление. Следовательно, при использовании известного фильтра в реальных условиях возникают дополнительные потери напора, обусловленные несовпадением направления и градиента фильтрации, снижаются эксплуатационные характеристики скважины.
Несовпадение оси симметрии отверстия и фильтрационного потока в отверстиях приводит к возникновению асимметричной нагрузки на арочные, мостовые структуры из частиц песка во
круг отверстий, что способствует снижению их устойчивости, периодическому разрушению и суффозии.
Скорости фильтрации в фильтр V возрастают от нижних к верхним отверстиям по зависимости
V = voch566^!, (5.4)
Где v0 - скорость фильтрации в нижних отверстиях фильтра или в сечении, на котором осуществляется приток; - диаметр фильтра (скважины); цп - гидравлический параметр фильтра
Dit
|
0,246 D* J |
|
(5.5) |
|
Q |
Ц N =—— arctg ^ 566l 6
J5 - разность пьезометрических уровней снаружи и внутри фильтра в конечном сечении; Q - расход через фильтр.
Увеличение скорости фильтрации в верхних сечениях фильтра и соответственно уменьшение в нижних вызвано перетеканием жидкости из нижних сечений пласта в верхние по мере фильтрации, т. е. наличием вертикальной составляющей скорости потока. Переток жидкости из нижних в верхние сечения пласта и фильтра, наличие вертикальной составляющей скорости фильтрации обусловлены перепадом давления между верхними и нижними сечениями пласта и фильтра, вертикальной составляющей градиента давления. Перепад давления на верхних отверстиях фильтра значительно выше, чем на нижних. Перепад давления на фильтре как функцию высоты отверстий можно определить, пользуясь известной формулой истечения жидкости из затопленного отверстия,
V = ц nV2 GJ 5. (5.6)
Приравнивая правые части выражения (5.4) и (5.6), получаем ! 566U.Nl [7. V
Voch = Ц Ч2 GJ5 ИФ
Или
J5 = ± f Vl ch566^. (5.7)
5 2G ^цN У~ D
Закон распределения перепада давления на фильтрующей оболочке по длине фильтра можно получить также, используя
Известную формулу зависимости скорости фильтрации от длины фильтра, подчиняющуюся закону гиперсинусов,
|
|
(5.8)
Где у - параметр распределения притока. Решая совместно (5.8) и (5.6), получаем
|
|
(5.9)
Преобразуя (5.9), получаем закон распределения давления по длине фильтра
|
|
(5.10)
Закон распределения перепада давления на фильтре по его длине может быть получен при обработке данных расходометрии с учетом выражения (5.4).
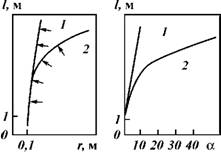
С помощью зависимостей (5.7), (5.10), на основании экспериментальных данных, реальных результатов расходометрии строят в масштабе эпюру распределения скоростей фильтрации по длине фильтра (рис. 5.1). По полученной эпюре с помощью выражения (5.6) и зависимостей (5.7) и (5.10) строят эпюру перепада давления на поверхности фильтра по его длине (рис. 5.2).
Поверхность постоянного давления в околоскважинной зоне может быть найдена различными способами, например методом гидродинамического, математического и физического моделирования или непосредственным расчетом. Метод непосредственного расчета основан на сопоставлении зависимостей (5.7), (5.10) и уравнения изменения давления по мере удаления от скважины. Характер изменения давления с расстоянием от скважины определяется выражением
|
|
(5.11)
Где т - вязкость флюида; K, K - коэффициент соответственно ламинарной и турбулентной фильтрации; т - мощность пласта; R - радиус влияния скважины; R - расстояние от оси скважины, на котором получено значение давления J5.
Режим фильтрации флюида в околоскважинной зоне оценивается по следующей методике. В случае ламинарной фильтрации давление в пласте по мере удаления от оси скважины определяется первым членом уравнения (5.11), а при турбулентной -
|
/, м |
|
Рис. 5.2. Зависимость длины фильтра от давления на него для разных режимов: 1 - ламинарный; 2 - турбулентный |
|
Рис. 5.1. Зависимость длины фильтра от входной скорости притока для разных режимов: 1 - ламинарный; 2 - турбулентный |
|
0І1И----------------------------------------- 0,01 р, МПа |
|
0,1 V, см/с |
Вторым. Поверхность постоянного давления определяется величиной радиуса R на некотором уровне фильтра, находящемся от нижних отверстий на расстоянии!, при котором давление остается постоянным. Зависимость R от L при J5 = const можно определить, приравняв правые части уравнений (5.7) и (5.11).
Для ламинарного режима получим
ПKmvL ch283UNl l
—Vo—_ch566unl = ln(r/r0), r = r0e, g0in)te ro J. (5.12)
2g (цп)2 Dф 2п Km
С учетом равенства (5.10) получим формулу поверхности постоянного давления в околоскважинной зоне, использовав гиперсинусоидальный закон распределения скорости по длине фильтра,
1 f sh у L l2 = t Q2
, , , , "h-: 2g ^ц N sh у J 4п2 Km ^
Sh у l
R = r0ete"shTJ. (5.13)
В случае турбулентного режима фильтрации имеем Vo ch 566 цNl = T Q2 f 1 _ 1
2g(цn)2 D^ 4п2 K'm2 ^ro r
R = 1 _ K'(ПMvO)2 ch 283Цп L (514)
Ro g t Q (ц n)2 ro ' '
Используя уравнение (1.9) для турбулентного режима фильтрации, получаем
1 f shyL l= tQ2 f 1 14
G ^ц n Sh YJ 4п2 k'm 2 ^ ro r
|
|
|
Рис. 5.3. Распределение постоянного давления в околоскважиннной зоне: 1 - ламинарный режим; 2 - турбулентный режим Рис. 5.4. Проволочный фильтр с профилированным сечением обмотки и изменяющимся углом наклона щели к оси каркаса: 1 - перфорированный каркас; 2 - опорные штыри; 3 - проволока |
R = 1 _ k^Г ShYl _2nmJ2 r0 2gті^цn shy Q J
Формулы (5.12)-(5.15) характеризуют закон распределения зоны постоянного давления как функцию длины фильтра и расстояния от скважины для ламинарного и турбулентного режимов фильтрации флюида в околоскважинной зоне.
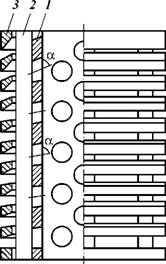
В масштабе строят поверхность постоянного давления в околоскважинной зоне (рис. 5.3). Проведя к полученной поверхности перпендикуляр к любой точке (эпюры на рис. 5.3), получаем направление градиента давления в данной точке (на определенном расстоянии от нижних отверстий), рациональное направление выполнения отверстий фильтра. Зная рациональное направление оси симметрии отверстий фильтра по его длине, получаем нужное расположение отверстий фильтра (рис. 5.4).
|
|
|
О |
|
(5.15) |
Рассмотрим пример подбора фильтра в конкретных условиях. Скважина вскрыла водоносный пласт мощностью 5 м, сложенный тонкозернистыми песками с коэффициентом фильтрации 1 м/сут. Расчеты показали, что при известной конструкции скважины при расходе 1 л/с наблюдается ламинарный режим фильтрации в околоскважинной зоне, а при расходе 2 л/с - турбулентный. При откачке с дебитом 0,8 л/с получаем характер изменения скоростей фильтрации и перепадов давления на фильт-
Ре (табл. 5.1). Рассмотрим участок фильтра в интервале от 0,85 до 1,45 м от нижних отверстий.
Закон распределения скорости по длине фильтра в этом случае описывается выражением (5.8) с параметром у = 1.
При использовании в расчетах удобных размерностей Q, л/с; l, м; K, м/сут; Д/5, м; т, м, рекомендуется использовать в формуле (5.11) переводной коэффициент 2,73. Тогда первый член равенства (5.11) можно представить как
2,73K l Д J5
Q = 2,73klAJ5; r/Го = ;
R0
2,73K l Д J5
R = R0 ■ 10 Q, (5.16)
Где r0 - радиус скважины у нижних работающих отверстий фильтра; R - радиус прифильтровой зоны выше нижних работающих отверстий фильтра, на котором наблюдается такое же давление, как и на удалении r0 у нижних отверстий.
Подставляя в уравнение (5.16) исходные данные, получаем
17,06Д J5
R = R0 ■ 10 Q. (5.17)
Расчеты по формуле (5.7) позволили определить распределение зоны постоянного давления по длине рассматриваемого интервала. Результаты расчетов представлены в табл. 5.1 в графе 5. Графа 4 характеризует перепад давления между различными сечениями фильтра. В графе 6 показана величина приращения радиуса прифильтровой зоны, на которую удаляется поверхность постоянного давления от скважины. Так, на интервале фильтра 0,85-0,95 м радиус зоны постоянного давления увеличился с 0,089 до 0,0925, т. е. приращение радиуса Дг = 0,0035 м.
|
Таблица 5.1
|
Угол наклона градиента давления и скорости фильтрации поверхности, перпендикулярной оси скважины и фильтра,
Ar
А = arctg —. (5.18)
Подставляя в уравнение (5.18) значения из табл. 5.1 (графа 6), получаем угол наклона градиента и скорость фильтрации к оси симметрии пласта а. Как показали расчеты, вектор скорости и градиенты фильтрации на интервале фильтра 0,85-1,45 м изменяет угол наклона к поверхности, перпендикулярной оси скважины и фильтра от 2 до 8°.
В этой связи целесообразно изменять направление отверстий фильтра по длине фильтра на участке от 0,85 до 1,45 м. На участке фильтра 0,85-0,95 м рациональный наклон отверстий к поверхности, перпендикулярной оси скважины и фильтра, составил 2°, на участке 1,15-1,25 м - 6°, а на участке 1,35-1,45 м - 8°.
В данных условиях целесообразно использовать фильтр, в котором ось симметрии отверстий наклона к поверхности перпендикулярной оси скважины под расчетным углом а. Оборудовали скважину новой конструкцией фильтра.
Рассмотрим турбулентный приток к фильтру на участке 0,850,45 м. При расходе 2,04 л/с в околоскважинной зоне наблюдалась турбулентная фильтрация. Характер распределения входных скоростей в фильтр и перепадов давления на отверстиях представлены в табл. 5.2.
Для удобства расчета второй член уравнения (5.11) преобразовали по аналогии с формулами (5.16) и (5.17):
AЛ = 9,7 • 10-3 ^-ij; _L-1 = 103,02AJ5. (5.19)
R = 1 -103,02 A J 5; r = [ ± -103,02 A J5 j. (5.20)
|
Таблица 5.2
|
Результаты расчетов по формуле (5.20) представлены в табл. 5.2 в графах 5 и 6. Угол наклона градиента и скорости фильтрации в околоскважинной зоне определяют по формуле (5.18) (см. графу 7).
На участке фильтра 0,85-1,5 м рациональный наклон отверстий фильтра к поверхности, перпендикулярной его продольной оси, изменяется от 2 до 64°.
Сопоставляя ламинарный и турбулентный режимы фильтрации флюида к скважине, становится очевидным, что при ламинарном режиме вектор градиента и скорости фильтрации, а также и рационального направления выполнения отверстий фильтра более плавно изменяет свое пространственное положение по длине фильтра, чем при турбулентном режиме.