Прогрессивные технологии сооружения скважин

ДВИЖЕНИЕ ПОТОКА В ФИЛЬТРЕ

Фильтры устанавливают в скважину с целью очистки добы­ваемого из пласта флюида от песка и других инородных приме­сей. Фильтр должен пропускать флюид и иметь при этом мини­мальное гидравлическое сопротивление, надежно предохранять скважину от проникновения твердой фазы, образования пробок и существенного снижения дебита.

В нашей стране и за рубежом разработано огромное число фильтров, что осложняет выработку единого подхода к гидрав­лике движения потока в каждой конструкции. Большинство за­висимостей базируется на известной формуле истечения из зато­пленного отверстия

О = цпЩ., (1.48)

V Р

Где V - скорость истечения из отверстия; ц - коэффициент рас­хода; N - скважность фильтра; J5 - перепад давления на фильтре; р - плотность флюида.

И. Петерсен, С. Ровер, М. Альбертсон предложили для опи­сания перепада давления на фильтре использовать закон гипер­болических косинусов

ХТ +1

' v (1.49)

Хт _ 1

Где т, D^ - соответственно длина и диаметр фильтра; % - гид­равлический параметр фильтра, характеризующий его конструк­тивные особенности.

По данным В. С. Алексеева параметр х равен произведению коэффициента расхода на скважность фильтра цп.

Определение цп по формуле (1.49) может дать удовлетвори­тельные результаты только для одного отдельно взятого отвер­стия. В случае оценки гидравлического параметра фильтра влия­ние отверстий друг на друга весьма существенно, что вносит в расчеты погрешность. Э. А. Грикевич рекомендует определять 54

Гидравлический параметр фильтра в лабораторных условиях по следующей формуле:

Цп = Дф arcth 566M

В представленной формуле предполагается, что расход Q че­рез фильтр по его длине m остается постоянным. На самом деле это может быть справедливо только для оценки притока в фильтры малой длины. Входные скорости притока в фильтр и расход через фильтр увеличиваются от нижних к верхним отвер­стиям согласно формуле Э. А. Грикевича

О = p0ch566^m, (1.51)

Где v0 - скорость притока в фильтр ниже рассматриваемого сече­ния.

С увеличением гидравлического параметра сопротивление фильтра уменьшается. Как показывают многочисленные экспе­рименты, параметр % изменяется от 0,19 до 0,88. Такой широкий разброс данных для фильтров однотипной конструкции объяс­няется разнообразием условий работы фильтров в реальных ус­ловиях и сложностью их классификации и типизации.

Поэтому прогнозировать реальное значение % в скважинных условиях с достаточной достоверностью сложно. Существенно изменяются гидравлические характеристики фильтра в контакте с породой. В. С. Алексеев получил данные разброса значений гидравлического параметра для фильтров одинаковой конструк­ции при контакте с породой различного гранулометрического состава (табл. 1.7).

Степень ухудшения гидравлического параметра фильтра при наложении частиц породы на отверстия определяется формой частиц и отверстия, соотношением их размеров. Установлено, что с увеличением окатанности и сферичности частиц плотность их

Сложения уменьшается и соответственно обеспечиваются улуч­шенные фильтрационные свойства слоя песка, контактирующего с фильтром. При вытянутой, продолговатой форме частиц про­исходит необратимая закупорка отверстий, уменьшение эффек­тивной скважности фильтра и резкое увеличение его гидравличе­ского сопротивления. Интенсивность закупорки зависит от фор­мы отверстия фильтра, находящегося в контакте с породой. Наи­более сильно эффект закупорки проявляется в сетчатых и про­волочных фильтрах, а также некоторых других конструкциях, предусматривающих расширение отверстий в направлении песка.

После установки фильтра в заданный интервал при подъеме инструмента возникает депрессия и порода продуктивного пласта обжимает фильтр; вокруг отверстий образуются своды естествен­ного равновесия. При освоении скважины и стимуляции притока на частицы, которые непосредственно прилегают к отверстиям, действует гидродинамическая сила, способствующая уплотнению частиц и частичной суффозии. Вследствие расширяющейся к породе форме отверстий при уплотнении породы возникает эф­фект «клина», приводящий к интенсификации снижения порис­тости и проницаемости прифильтрового слоя породы. Часть час­тиц породы выносится через отверстие, а другая часть закупори­вает поры и цементирует естественный скелет породы, контакти­рующей с отверстием.

Степень уплотнения породы и цементации отверстия зависит от количества расклинивающих граней. В случае проволочного фильтра таких граней две, а в случае сетчатого покрытия - че­тыре. Функцию расклинивающих граней может выполнять не только фильтрующее покрытие, но и поверхность уже заклинив­шихся в отверстиях частиц. При застревании частиц в отверсти­ях расклинивающий эффект в существенной степени ухудшает гидравлические параметры фильтра.

При каптировании продуктивных пластов, сложенных разно - зернистыми песками, избежать расклинивания породы в отвер­стиях фильтра очень сложно из-за самых разнообразных соотно­шений размеров отверстий и частиц. Крупные фракции застре­вают в отверстиях, мелкие в процессе откачки цементируют по­ристое пространство, снижая проницаемость контактной зоны. Некоторые конструкции фильтров предусматривают работу от­верстий без контакта с породой. Это фильтры с коническими от­верстиями, гравитационные и тарельчатые конструкции. Указан­ные типы фильтров предусматривают образование сводов равно­весия из частиц в процессе устойчивой работы. В реальных ус­ловиях своды равновесия при изменении режимов эксплуатации периодически разрушаются, что приводит к проникновению 56

Внутрь фильтра песка или гравия и заклиниванию отверстий. В этой связи избежать закупорки отверстий породой сложно, хотя расклинивающий эффект, снижающий проницаемость зоны, воз­можно предотвратить.

Закупорка отверстий породой наиболее интенсивно происхо­дит в интервалах фильтра, характеризующихся максимальными скоростями притока. Поэтому в процессе освоения скважины и стимуляции притока гидравлическое сопротивление фильтра за счет контактных потерь будет изменяться, увеличиваясь в наибо­лее обильных интервалах и оставаясь приблизительно постоян­ным в менее обильных. Процесс закупорки отверстий породой продуктивного пласта способствует выравниванию эпюры вход­ных скоростей по длине фильтра. Однако выравнивание скоро­стей достигается за счет снижения притока в перспективных ин­тервалах и не способствует получению больших дебитов.

Гидравлический параметр фильтров % = цп считается величи­ной переменной и изменяющейся по длине фильтра в зависи­мости от состава, свойств контактирующей породы и режимов притока.

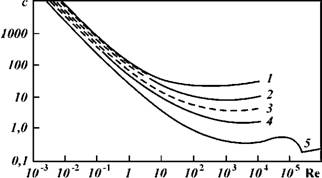
Из гидравлики известно, что коэффициенты сопротивления с Меняются с изменением режима движения потока, характери­зующегося числом Рейнольдса (рис. 1.14). С увеличением скоро­сти движения потока коэффициент сопротивления уменьшается. Следовательно, по длине фильтра коэффициент сопротивления или гидравлический параметр будет меняться даже при одинако­вом эффекте наложения частиц. Измеренный в лабораторных условиях гидравлический параметр %, рассчитанный по формуле (1.50), носит обобщенный характер и справедлив только для об­разца модели заданной длины в испытуемых режимах и только при контакте с аналогичной породой. Обеспечить такое подобие почти невозможно, поэтому переносить расчетный по данным эксперимента гидравлический параметр с достаточной степенью достоверности в реальные условия нельзя.

Рассмотрим обобщенную модель движения потока в фильтре в общем виде. Закон сопротивления при обтекании потоком лю­бых тел описывается зависимостью

Fc = флц^ + фтр d 2v2, (1.52)

Где Fc - сила гидродинамического сопротивления; фл, фт - коэф­фициент соответственно ламинарного и турбулентного сопротив­ления обтеканию; D - размер структурного элемента фильтра; ц, р - соответственно вязкость и плотность пластового флюида; V - Скорость обтекания.

57

Перепад давления на обтекаемом элементе фильтра можно определить из выражения (1.52)

Ф лц» 2

J5 = + ф Tpv.

Решая квадратное уравнение (1.53), получаем общий вид за­висимости скорости от перепада давления на фильтре

V = J^JU + j - i^JL. чфт 2pd J фтр 2 фт pd

При ламинарном потоке скорость истечения через фильтр оп­ределяется только линейным членом

V = dJ 5/ ф!^ (1.55)

А при турбулентном истечении - квадратичным членом

(1.56)

Нельзя рассматривать только ламинарный или только турбу­лентный режим истечения из отверстий в фильтре, так как обычно наблюдается и тот и другой режим в разных сечениях. Ламинарный режим характерен для областей с низкими скоро­стями фильтрации (в нижних интервалах фильтра), а турбулент­ный - для интервалов наиболее обильного притока.

Сопоставляя выражение (1.48) с равенствами (1.55) и (1.56), можно сделать вывод, что % = цп в зависимости от режима 58

Фильтрации будет меняться от значений % = ^фт1 (турбулент­ный режим) до х = р J5 (ламинарный режим).

Установить значения цп для фильтра данной конструкции сложно. В этом случае оправдано пользоваться коэффициентами сопротивления для ламинарного и турбулентного режимов фильтрации фл фт, каждый из которых в своей области досто­верно описывают процесс движения потока в фильтре.

Рассмотрим потери напора в фильтре с учетом изменяющихся типовых скоростей потока по длине по закону гиперболических синусов или тангенсов [см. равенства (1.41) и (1.42)]. Уравнение силы сопротивления (1.52) с учетом изменяющихся скоростей имеет вид

Fc =Ф Л т2 v( z) + Ф т рт 4 v 2(z X

Где v(z) - функция скорости по длине фильтра z.

Дифференцирование выражения (1.57) дает следующие выра­жения:

Для гиперсинусоидального закона

Dv v а і ( z І

V(z) = —= ——chІ а— J;

Dz m sh — I m

Для тангенциального закона

Подставляя уравнения (1.58) и (1.59) в равенство (1.57), по­лучаем уравнение распределения силы сопротивления по длине элемента фильтра для типового характера распределения скоро­стей.

По гиперсинусоидальному закону

Ch І - —

Фл цт + фт Pm2v — •

По тангенциальному закону

59

Перепад давления на элементе фильтра с учетом изменяю­щихся скоростей притока выражается следующими зависимо­стями:

Для гиперсинусоидального закона распределения скоростей по длине фильтра

Chl а —

Ц , — V m

Фл - + Фт Pv а ----------

M sh а

Для тангенциального закона распределения скоростей по дли­не фильтра

Y л ^ +

M

Tg ycos2 [ y — M

В интервале ламинарного притока распределения перепада давления на элементе фильтра по его длине удовлетворительно описываются следующими уравнениями:

J5 =

Mtg y cos2 [ y — M

Или

Юл цю аЛІ а —

J5 = V m

MSh а

Для турбулентного притока уравнения (1.64) и (1.65) имеют

Вид

—2 2

Т = VXPv Y

J 5 = -------- 7Т~г

Tg ycos l y— V m

Ch2 [ аz

(1.63) по радиусу для радиального притока к фильтру, получаем уравнения для определения перепада давления на фильтре лю­бой конструкции

Ch I — —

ФлЦІП — + фтР—

2п shc

J 5 = —

2nm[1]Tg у cos2 I y —

Где r4, r5 - соответственно больший и меньший радиусы фильт­ров, разность которых соответствует толщине фильтра.

Основными параметрами, характеризующими сопротивление фильтра в уравнениях (1.68) и (1.69), считаются коэффициенты ламинарного и турбулентного сопротивлений обтеканию фл и фт. Значения параметров фл и фт, легко получить в лабораторных условиях, а затем использовать в реальных условиях. В этом случае применение двух коэффициентов позволяет охватить практически всю область режимов фильтрации в фильтрах и из­бежать погрешностей в расчетах. Проводя эксперименты на фильтрационных лотках при малых скоростях притока на всей длине образца при значениях числа Рейнольдса меньше критиче­ских и зная перепад давления на фильтрах J5, получаемый по разнице показаний пьезометров, с помощью формулы (1.55) оп­ределяют коэффициент ламинарного сопротивления обтеканию фл. При установлении на лотке на всей длине образца турбулент­ного режима фильтрации в фильтре по формуле (1.56) находят коэффициент турбулентного сопротивления фт. Параметры не­равномерности притока по длине фильтра — и y определяются по методике Э. А. Грикевича на основании экспериментов.

Значения гидравлических сопротивлений фл и фт могут быть найдены из реальной расходограммы. Основной закон сопротив­ления (1.53), включающий члены, пропорциональные скорости и квадрату скорости, имеет два неизвестных коэффициента сопро­тивления фл и фт и скорость. Перепад давления на фильтре изме­няется пьезометрами. Подставляя в уравнение (1.53) реальный

61

Закон распределения скоростей притока по длине филмра, полу­чаем

Shl a —

Фл^ + Фі Pv -

AT4

Устанавливая ламинарный режим фильїрации на модели на всей длине образца, при которой квадратачныш член в (1.70) близок к нулю, получаем уравнение для определения коэффици­ента ламинарного сопроіивления

Ф = _A_T4J5sh a

JovshI a—

Если иніенсифицироваїь приток на модели и усіановиїь іур - булен1ный режим фильїрации по всей длине образца фильїра, іо линейный член в уравнении (1.70) будеї близок к нулю. То­гда коэффициен! іурбуленіного сопроіивления фильїра

(172)

—2 і 2 l — pv sh I a—

В случае, когда приток в фильір лучше описывается іанген - циальным законом выражения (1.71) и (1.72), можно записаіь

Ф = 2t4J5tg Y .

Цс tg | y— M

Tg2 И,

X т =ф = J ; (1.75)

Tg2Y pv2

Tg I Y — I

L m I 2R4 J5 nc.

X ё = Фл ;g 1 = (1.76)

Tg Y Н»

При решении задач по определению перепада давления на фильтре неравномерность притока сложно учитывать введением в выражения (1.75) и (1.76) тангенциальных и гиперсинусои­дальных сомножителей. В этом случае может быть применен па­раметр, равный произведению коэффициентов ламинарного и турбулентного сопротивлений на параметр неравномерности притока — или y. При ламинарном режиме притока коэффициент сопротивления умножается на параметр неравномерности — или Y в первой степени и при турбулентной фильтрации - на их квадрат. В выражениях для определения перепада давления на фильтре (1.62)-(1.69) присутствуют параметры хт = флY2 = фл—2 и Хт = ФлY = фл—, что упрощает расчеты.

Фильтр редко состоит из однотипных по длине и толщине элементов обтекания. Обычно конструкция включает фильтрую­щую оболочку, каркас и промежуточные звенья. Поэтому теоре­тически правильнее было бы выделить из обобщенных коэффи­циентов или гидравлических параметров составляющие сопро­тивлений фильтрующей оболочки, каркаса, промежуточных звеньев и учесть влияние одних элементов на другие, стесненные условия обтекания. Однако на практике это не приведет к суще­ственному шагу вперед из-за сложности точного теоретического и экспериментального выделения разных составляющих сопро­тивления и оценки их реального вклада в общий результат.