НАНОТЕХНОЛОГИЯ В БЛИЖАЙШЕМ ДЕСЯТИЛЕТИИ

Изменения масштабов (скейлинг) и проблема усложнения расчетов для наносистем при таких изменениях

Д. Диксон[10]

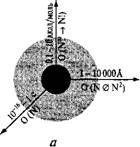
В методах расчета характеристик наносистем на ЭВМ одной из главнейших яв­ляется проблема масштабирования (скейлинг, изменение масштабов), кото­рая, как показано на рис. 2.1, а, должна рассматриваться в трех различных аспектах или измерениях. На рис. 2.1, а и 6 указаны экспериментальные и рас­четные методы, используемые при изменениях временного и пространствен­ного масштабов соответственно [1].

На рис. 2.1, а ось «Размер» представляет диапазон изменений масштаба в исследуемой области, а именно от размеров атома (~ 1 А) до размеров наноча­стиц (~ 1 мкм). Расчеты химических свойств требуют, например, учета куло - новского взаимодействия при изменении масштаба от N до N2. В таких расче­тах разложение в ряд проводится до члена O(NlgN), где N— число частиц. Ось «Время» соответствует динамическому (временному) изменению масштаба событий. Хотя изменение масштаба по этой оси является линейным, однако сам диапазон изменения очень широк, так как время изучаемых процессов меняется на 15 порядков величины, от 1 фс (Ю-15 с) до 1 с, что является, одна­ко, недостаточным для многих медленных макроскопических процессов. По оси «Точность» показаны соответствующие изменения точности расчетов и измерений.

Повышение точности расчетов представляется необходимым условием как для разработки принципов конструирования материалов и понимания сущно­сти протекающих в них явлений, так и для сокращения числа сложных и доро­гостоящих экспериментов. В настоящее время уже существуют возможности

Время t Квантовая механика Молекулярная динамика

_ Уравнение Ланжевена

Кинетика процессов перескока, обобщенная теория Ланжевена,

^ уравнение Больцмана для решеточных систем_______________

+

1 фс 1 ПС 1 не

Сверхбыстрая спектроскопия

Оптические и колебательные спектры

^Диэлектрическая и механическая релаксация Химическая кинетика

Магнитный резонанс

1 МКС

Временные масштабы б

Электронная структура, Молекулярная механика/динамика

. Процессы перескока, модели с «огрублением», аналоги

0,1 нм

Колебательная спектроскопия, ЯМР, рентгенография, нейтронография, получение изображений

Брэгговское отражение Строение клеток

СЭМ, ПЭМ

| Ковалентный синтез Методы

Сборка кластеров получения

^ Обработка, модификация структур

Пространственные масштабы

Рис. 2.1. Масштабы процессов в системах наночастиц и степень сложност соответствующих молекулярных расчетов.

Преодоления классического предела так называемой «химической точности», равного 1 ккал/моль.

Как видно из рисунка, зависимость точности расчетов от числа частиц в системе является очень сложной и создает много проблем. Попробуем выразить эту задачу через число базисных функций исходя из того, что для опи­сания каждой частицы требуется задать от 50 до 100 таких функций. При изме­нении масштаба это число обычно возрастает как Nm (для особо точных расче­тов т = 7), но может доходить и до № (например, для полного учета всех конфигурационных взаимодействий). Даже точность порядка 5—10 ккал/моль требует расчетов ст = 5, поэтому переход к большим размерам и временам тре­бует, при сохранении достаточной точности расчетов, использования более мощных вычислительных средств.

Хотя некоторые задачи, связанные с поведением наночастиц, могут быть ре­шены уже на современном уровне вычислительной и экспериментальной тех­ники, надо отметить, что для решения большинства важных проблем в этой об­ласти пока не существует хорошо разработанных общих подходов. На рис. 2.1,5 и в представлены методики, которые могут быть использованы для изучения структуры и свойств наночастиц в различных временных и пространственных масштабах. Наряду с многочисленными экспериментальными методами иссле­дования наночастиц предложены и разнообразные теоретические и расчетные методы их описания. На рис. 2.1, б представлены временные интервалы, харак­терные для некоторых режимов, описываемых динамическими теориями.

Методы моделирования молекулярной динамики применимы для исследо­вания ограниченного числа локальных и быстрых процессов, однако они мало­пригодны для полномасштабного описания реального поведения изучаемых систем. Классическая молекулярная динамика во многих случаях не примени­ма по той причине, что времена релаксации в конденсированных системах (например, в полимерах) могут составлять от нескольких пикосекунд до не­скольких часов. В качестве альтернативы можно прибегнуть к «огрублению» масштаба и рассматривать движение типа броуновского, для описания которо­го подходит уравнение Ланжевена. Очевидно, что заметного прогресса в этом направлении можно добиться либо объединением различных теоретических подходов, либо разработкой новых. В то же время следует развивать и существу­ющие методы и распространять их на более крупные системы и более длитель­ные процессы. В качестве примера можно отметить удачное использование ме­тодов линейного увеличения масштаба в квантовохимических расчетах или применение методов многоступенчатых временных шагов в молекулярной дина­мике (с соответствующей аппроксимацией) при оценке дальнодействующих сил.