Моделирование миграции подземных вод
Миграционная модель обезжелезивания в подземных водах
В качестве примера приведем построение системы уравнений, со - ставляющих теоретическую модель процессов обезжелезивания подземных вод[10]. Эта задача актуальна в связи с широким распространением подземных вод, в которых содержание железа превышает норматив 0,3 мг/л, установленный ГОСТ 2874—82. Зарастание водопроводной и водоразборной арматуры железистыми осадками, неудовлетворительные органолептические показатели воды, а также требования к ее качеству в бумажной, текстильной, пищевой и других отраслях промышленности обусловливают необходимость значительных капитальных затрат на водоподготовку. Одним из перспективных методов очистки воды от железа является его удаление непосредственно в подземных условиях. Суть метода заключается в том, что в водоносном горизонте при подаче кислородсодержащих вод создается зона осаждения соединений железа, через которую фильтруется и откачивается подземная вода. По мере связывания кислорода растет содержание железа в откачиваемой воде, что требует повторной зарядки этой зоны кислородсодержащими водами. В результате окисления Fe2+ и частичного гидролиза в поровом пространстве пласта образуются гидроксиды железа (II), (III), обладающие значительной способностью к сорбции на породах. Кроме процессов сорбции на извлечение из воды понов закисного железа влияют также железобактерии, для жизнедеятельности которых не требуются высокие содержания кислорода и органических веществ [26].
Обоснование модели и прогнозирование процесса обезжелези - вания воды — сложные задачи. Их можно решить с некоторыми допущениями, суть которых будет определена при описании моделей отдельных процессов. Будем рассматривать условия, когда свойства рассматриваемых подземных вод отвечают значениям рН 6,5, рЕ 0 при содержаниях Fe2+c и растворенного КИС-
^тах
Лорода в нагнетаемой воде Рассчитаем концентрации
Fe2+, Fe3+ и 02 в грунтовой воде в зависимости от времени t и координат в плане при любых режимах закачки и откачки.
При малых градиентах напора естественного потока примем поток вблизи скважины планово-радиальным, а строение пласта мощностью т однородным, так что скорость фильтрации vr на расстоянии г от скважины с дебитом Q можно определить по уравнению
= Q/(2nmr). (5.5)
Эта модель является удовлетворительной аппроксимацией в условиях напорного потока грунтовых вод вблизи скважины, обоснование ее применимости можно получить из решения для скважины в естественном потоке [см. уравнение (6.4)].
При построении миграционной модели будем исходить из цепи •образных моделей (рис. 15). Предположим, что в основной массе породы не происходит никаких процессов обмена (нет связи между Gf и G", см. рис. 15,в), так как мигранты практически не транспортируются через породу. В качестве мигрантов будем рассматривать три компонента, связанные согласно уравнению окисления Fe(II): катион F2+ = Fe(II), растворенный в грунтовой воде кислород 02 = 02(в) и коллоидально растворенный или суспензированный Fe(OH)3 (в виде хлопьев). Образующийся ион водорода Н+ не рассматривается вследствие предполагаемых хороших буферных свойств системы.
Концентрация веществ в жидкой с0 и твердой (неподвижной) N фазах в этом примере будет выражаться в массовой (ммоль/дм3) и эквивалентной (сэ=гс0, N3—zN) формах.
Мигрант Fe2+. Процессы переноса. Закисное железо Fe2+ переносится потоком подземных вод посредством конвекции и дисперсии, так что плотность переноса иПре представляется выражением
^ dC°Fe Vr
Ип D—. (5.6)
"Fe дг 1 П0 °Fe 1 '
Процессы обмена и накопления. Перераспределение Fe2+ между грунтовой водой и основной массой породы происходит путем ионного обмена. Этот процесс рассматривается в данном примере как равновесная реакция между жидкой фазой 0 и частью породы
|
|
|
S®j Шш |
|
Н................ н |
V.. Л -
*
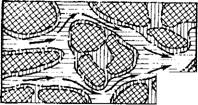
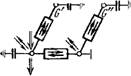
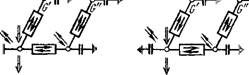
Многоступенчатая цепь наглядных моделей миграции железа Fe2+, кислорода 02 и гидроокиси железа в грунтовых водах.
4х — схематический разрез породы; б — схема стыковки фаз породы для описання процессов межфазового обмена; в — кибернетическая схема обмена мигрантов между фазами; г — кибернетическая схема процессов превращений.
G', между неподвижной жидкой фазой Н и частью породы G". В итоге получаем и рассматриваем только две фазы — подвижную О и неподвижную Н (см. рис. 15, г).
Способность неподвижной фазы к накоплению можно представить как таковую для части породы (G"=pG) и для неподвижной воды. Последней составляющей для многих пород можно пренебречь, а лучше всего прибавить ее к подвижному потоку подземных вод. Соответственно способность подвижной фазы к накоплению представим как для части породы (G'—aG) и движущейся неподвижной воды (см. рис. 15,г).
Емкость катионного обмена (ЕКО) твердой фазы (в особенности части рС) растет при обезжелезивании вследствие начала отложения гидроксида железа (III). Это явление зачастую обусловлено биологическим окислением Fe(II) вследствие роста биомассы в неподвижной фазе.
Рассмотрим теперь конкретный пример расчета, предполагая емкость катионного обмена постоянной — ЕКО—14,2 ммоль на
|
Рис. 16. Изотермы Генри и Ленгмюра для эквивалентной массы Fe2+ на единицу объема породы для подвижной и неподвижной фаз. / — изотерма Леигмюра согласно уравнению (3.2); 5 —изотерма Генри согласно уравнению» (3.1); 3 —емкость катиоиного обмена (240 ммоль/дм3) |
100 г породы. При объемной массе скелета породы 1,7 г/см3 получим величину емкости катионного обмена 240 ммоль/дм3. В условиях термодинамического равновесия эквивалентная масса катионов в грунтовой воде составит 1,5 ммоль/л. При заполнении водой части объема с я0=0,26 это составило бы 0,4 ммоль/дм3 горизонта грунтовых вод. Если к каждому литру такой воды добавить, например, 20 мг Fe2+, его эквивалентная масса составит (2-20 мг/л)/(56 мг/ммоль) =0,7 ммоль/л или 0,2 ммоль/дм3. Это* была бы всего лишь треть эквивалентной массы катионов в подземной воде, которая для данного примера могла занять при термодинамическом равновесии около 1/6 емкости катионного обмена, т. е. возможная эквивалентная масса вещества составит 40 ммоль/дм3.
Как видно из рис. 16, распределение катионов между водой и основной массой породы в этой области довольно точно описывается изотермой Генри. При содержании железа в грунтовой воде 40 или 50 мг/л это распределение естественно изменилось бы. Изотермы Генри или Ленгмюра, описывающие неравновесные процессы обмена, можно представить в виде [см. уравнение (3.2) и (3.7) ]:.
Равновесные условия Неравновесные условия
Изотерма Генри *3Fe = *<*сэ0ре - (А - Z)Fe = «/ [Кас0ре - Npe),
Kd=200 (см. рис. 16) где А и Z — скорости прямой и обрат
Ной реакций обмена (адсорбции и десорбции) ; ак'=ак/Кл — константа скорости обмена
Изотерма Ленгмюра _ ^Qpe (A-~Z)p^aK' I7EKO-АЦ с^-
^Ре- 1,0 + 0,8331 " _KN
Где ЕКО=240 ммоль-экв/дм3 и Kd! ЕКО=200 : 240=0,833.
Конкретные модели накопления и обмена получим соответственно рис. 16 и выражению c3=zc\-
Для удельного накопления Sh и So (в неподвижной и подвижной частях):
TOC \o "1-3" \h \z - shfe= ^fe = Р200соре; (5.7)
Или (при изотерме Ленгмюра)
_ 3200
SHFe— C0Fe р +о,833сэ0ре
І. . я200
= с0 і 1 +
Fe "Fe 1 1 + 0,833сэ0
\ Fe
Обмен
DN? ejdt = а/ (р200с0ре - N? e
Или __
DNv. ldt = а/ (0,833 (то - <?0ft - Af.),
Где а и р — безразмерные параметры разделения.
Процессы превращения. Превращение Fe2+ вследствие окисления протекает в две стадии. Уравнения их стехиометриче - ского баланса и реакции в целом имеют следующий вид [см. уравнение (2.13)]:
Биологически
4FeJ+ + 03 + 4Н+ -------------------------- 4Fe3+ + 2Н20 + энергия
Химически
4Fe3+ + 12НаО ------------------------ •-> 4Fe (ОН)3 + 12Н+
4Fe2+ + 03 + 10Н2О--------------------------------- > 4Fe (ОН)3 + 8Н+ + энергия '
Скорости превращения при этих условиях можно получить, например, по уравнению
Г Fe =К [Fe2+] [02] = K*cPecQi. (5.9)
Рекомендуется также следующее уравнение реакции:
Г Fe = Kr [Fe2+] [02]/[Н+]2 =/Г [Fe2+] [02] [ОН-]2,
Которое переходит в уравнение (5.9), если значения рН, а следовательно, [Н+] и [ОН-] остаются постоянными (это предполагается в данном примере).
Мигрант 02. Процессы переноса. Растворенный кислород переносится потоком подземных вод аналогично закисному железу Fe2+ [см. уравнение (5.6)]: де» •
"■о.—
Процессы обмена и накопления. Растворенный кислород накапливается в подвижной и неподвижной воде и обменивается между обеими фазами. При таких предпосылках запишем следующие модели процессов накопления и обмена:
S0 = ще, , sH = пИсн, (5.10)
Oj Oi U2 U!
Где no и ян — пористость, относящаяся соответственно к подвижной и неподвижной воДе, причем в условиях равновесиями — С0
Оа Оз>
А в неравновесных условиях имеет место соотношение (A~Z)о== KoJc0 ~сн
^ Ua Ua
Где Ко.} — константа скорости обмена 0%.
Процессы превращения. Скорости превращения для кислорода, вероятно, соответствуют скоростям превращения закисного железа. Согласно стехиометрическому балансу, 4 моля Fe2+ всегда реагируют с 1 молем 02, так что при выбранном допущении имеем:
Г0 = 0,25га, - 0,25АГ*сРеСо2. (5.11)
Кроме того, следует оценить потребление кислорода на окисление других веществ в подвижной и неподвижной фазах. Если последние рассматривать в целом, то можно представить два предельных случая.
1. Притекающая грунтовая вода не имеет в своем составе никакого кислородпотребляющего вещества, кроме Fe(II). При первом поступлении кислородсодержащего инфильтрата окисляются все неподвижные кислородпотребляющие вещества. При повторном поступлении такого фильтрата в тот же водоносный пласт выполняется уравнение (5.11), так как никакого дополнительного потребителя Ог больше нет,
2. Количество окисляемого вещества считается столь большим, что оно практически не уменьшается вследствие окисления растворенным кислородом инфильтрата. В этом случае получаем выражение для дополнительного потребления кислорода в неподвижной фазе:
Для рассматриваемого примера используется также соотношение Г о, = (<р/4) Г Fe,
Где ф>1. Величина коэффициента <р для первой порции фильтрата выбирается наибольшей и в последующем должна асимптотически стремиться к предельному значению.
Мигрант Fe(OH)3. Процессы переноса. Коллоидально растворенные или суспензированные частицы Fe(OH)3 переносятся потоком подземных вод вследствие конвекции и дисперсии [см. уравнение (5.6)].
Процессы обмена и накопления. Предположим, что частички Fe(OH)3, образующиеся на основкой массе породы, не растворяются, а отлагаясь (накапливаясь), остаются на месте (см. рис. 15, г). Микрохлопья, образующиеся в неподвижной воде, тотчас сорбируются породой и не обмениваются в потоке подземных вод.
Гидроксиды железа (III), отлагающиеся на основной массе породы, «стареют» (дегидратируются) в две стадии:
FefOH Fe = О
,0
-------------- > ли -4" н20 ---------------------- —>■ /0 -}- ЗН20
•стадия 1 ип стадия 2 Рр/
/он / Л S>
FefOH Fe = 0
Х0Н
A-FeOOH (гетит) Fe203 (аморфный)
P-FeO. OH (лепидокрокит) Fe203 (кристаллический)
Вследствие этого процесса растет их плотность и снижается объем. Поэтому в данном примере можно предположить, что на фильтрационную проницаемость не влияет осаждение Fe(OH)3, FeOOH или Fe203, т. е. миграционные процессы не влияют на модель фильтрационного потока. Это предположение можно дополнительно лроверить для конкретных случаев расчетами объема выделившихся осадков. Таким образом, для мигранта Fe(OH)3 получим ^следующие модели процесса накопления:
Sn = tlnCn : sh :== Си
Fe (ОН)з и °Fe(OH)3' Fe (ОН)з nFe (ОН)3
И обмена [согласно уравнению (3.8)]:
^Fe (ОН),= #осС0ре(ОН)і
Процессы превращения. Скорости превращения для Fe(OH)3 удовлетворяют закономерностям, которые были установлены для Fe2+. Согласно уравнению (5.9), реагируют 4 моля Fe2+ и 4 моля Fe(OH)3, так что, при выбранном подходе, согласно уравнению (5.9),
>*Fe СОН), — ГРе = K*Cfsc0i.
Общая миграционная модель (см. рис. 15, г) состоит из системы шести дифференциальных уравнений с шестью зависимыми
Переменными (концентрации в пересчете на единицу объема водоносного горизонта):