ПРИМЕНЕНИЕ ЖЕЛЕЗОБЕТОНА МАШИНОСТРОЕНИИ
Приближенный метод расчета толстой торообразной оболочки, находящейся под действием внутреннего давления
Основным недостатком приведенных формул для расчета горообразных оболочек является то, что они не позволяют установить закон распределения тангенциальных напряжений в поперечном сечении спиральной камеры, так как эти напряжения, как и в обычном цилиндре, считаются равномерно распределенными по сечению. Для металлических спиральных камер этот фактор не играет существенной роли, поскольку подбор толщины оболочки производится по меридиональным напряжениям, величина которых примерно вдвое больше тангенциальных.
В железобетонных спиральных камерах закон распределения тангенциальных напряжений влияет на характер армирования конструкции, а поэтому возникает необходимость уточнения расчета.
Вырежем из толстостенной торообразной оболочки бесконечнб малый элемент, образованный углами гіф (фиг. 2, а) и гі0 (фиг. 2, б) и поверхностями, отстоящими от центра сечения на расстоянии гх и Rx + Drx. Введем предположение, что перекоса элемента не происходит и по его граням действуют только нормаль
Sin ф
Dr.
Из которой следует, что ~ =
ЙГл
1, т. е. dr2~ drx
_ Drx
Для упрощения дальнейших записей отбросим индекс у радиуса кривизны гх. Тогда будем иметь
Dr2 — dt\ — dr. (12)
|
Ные напряжения ооф и |
Составим условие равновесия элемента тора, спроектировав все силы на направление радиуса г:
|
Dy |
|
Dr dQ |
(ог - dor) (г + dr) гіф (г2 - I - dr) dQ вгг гіфг2 dQ — (сгф + гісГф)^ r2 + —
2cr« Dr
После приведения подобных членов, сокращения на общий множитель гіфгіб и пренебрежения малыми величинами высших порядков будем иметь
Do, rrt - I - or dr (г2 -
|
Г) — Оф drr2 — Од drr — О |
|
(13) |
|
■о»)- |
(Or
Полученное выражение является условием равновесия бесконечно малого элемента торообразной оболочки. Нетрудно заме -
Тить, что прй 12 -> со это выражение превращается в условие равновесия толстостенного цилиндра:
^ + K-V> = 0, (14)
А при r2 = г получается условие равновесия толстостенной сферической оболочки:
Fgr + 4-(a,-a,) = 0, (15)
Где меридиональное напряжение огф равно тангенциальному ae.
Поскольку уравнение (13) содержит три неизвестных величины Ог, ОГф и 0Г9, то для решения его необходимо составить условия совместности деформаций. Будем считать, что грани элемента, плоские до деформации, остаются плоскими и после деформации, т. е. перемещение всех точек элемента определяется величиной радиального перемещения U точек внутренней поверхности элемента (фиг. 3). Точки внешней поверхности элемента перемещаются в радиальном направлении на величину U + DU, а толщина элемента изменяется на DU.
Тогда относительная радиальная деформация будет
DU Фиг. 3. Деформации беско-
Ег = - jp. нечно малого элемента тора.
І
В меридиональном направлении относительная деформация элемента еф определяется относительной деформацией дуги АА1У Которая в деформированном состоянии займет положение А 'А\\ При этом єф = Аналогично получается величина относительной деформации в тангенциальном направлении. Эта деформация равна е9 = ^г.
Выразим относительные деформации через напряжения по закону Гука:
TOC \o "1-3" \h \z Ег ~ — (°г М^ф М^е); (16)
ЕФ = -7- = К — l1^)- (17)
|
|
Е9 = = ——ЦОф)- (18)
Полученные выражения совместно с уравнением равновесия позволяют найти четыре неизвестных величины: ог, огф, о9 и U. Исключим из уравнений величины напряжений и получим дифференциальное уравнение для определения перемещения U. Для этого возьмем ог9 из выражения (17), выразим:
1 EU
И подставим полученное значение о9 в уравнение (16):
DU 1 ( , EU\
= ~Ё~\аг —~ 0гф + fior, + — J
ИЛИ
|
DU dr |
|
(20) |
|
(Р г — |
U 1+j. i
Е
Подстановка значения о9 из уравнения (19) в уравнение (18) дает
|
JL (г |
|
Ог- |
U __ і UE
77 ~"Т
ЦОг — и^огф
Или
|
(1-ю И |
|
(21) |
И (цг + г2) __ 1 + ц
Ц/т2
Сложив левые и правые части выражений (20) и (21), исключим из них напряжения 04:
|
Аф] ' |
|
°ч> — |
1+ц Г (1-Ю
MJ __ . U (цг + г2) dr г ' цгг2
Подставив полученное значение оф из уравнения (22) в уравнение (20), получим выражение для определения ог;
|
Ец |
|
U |
|
(23) |
|
Dr |
|
(1 +|і)(І-2,І) |
(1 — ц) dU R + R2
Найдем значение^, продифференцировав выражение (23):
DOj. __ Ell Г(1 — ц) D4J_
|
R[17] + r22 |
Dr ~~ (1 4-И) (1 — 2ц) ц • Dr2 +
(1 4- ц) (1-
|
U |
|
+ |
|
Dr |
T 4- r2 dU
(24)
Выражение для o9 получим, подставив значения огф и ог из уравнений (22) и (23) в уравнение (19):
П \dU і. — + R / ;1
0 (1 + ц) (1 — 2ц) [ Dr Т" цг2г J"
Таким образом, с помощью зависимостей (22), (23) и (25) можно определить напряжения ог, огф и ог9, если известно перемещение U. Для определения U необходимо исключить значения напряжений и производной от радиального напряжения из уравнения равновесия (13). После соответствующих подстановок и преобразований получаем дифференциальное уравнение
L№ r + r2 dU r2A-rl
77- "і----- —— —---------- (26)
Dr2 ггг dr Rr^
Таким образом, для определения U получили обыкновенное, линейное дифференциальное уравнение второго порядка с переменными коэффициентами. Если использовать зависимость (11) между радиусами кривизны торообразной оболочки, то получим окончательно
D2U А + 2R Sin ф DU Г г r sjn ф^ • Dr
_ a2 -F 2г (а + г Sin Ф) Sin Ф jy = q ^7)
R2(A-\-R sin ф)2 ' ' '
Это уравнение при а ^ со превращается в дифференциальное уравнение Эйлера второго порядка для толстостенного цилиндра:
- = (28)
А при а = О получаеігся уравнение
Г2 ~ + 2R ^ — 2U 0, (29)
Аналогичное уравнению (28) и описывающее напряженное состояние толстостенной сферической оболочки.
Таким образом, для получения выражений, определяющих напряжения ог, огф и а9, необходимо найти решение дифференциального уравнения (27) и удовлетворить полученное решение условиям на поверхности оболочки. Эти условия в случае оболочки, находящейся под действием внутреннего давления р, Будут
TOC \o "1-3" \h \z при Г - Q, ог --- —р\ (39)
При /- = .£> о г = 0. (31)
Значения ог могут быть найдены из дифференциальной зависимости (23), если известно выражение для U, полученное из уравнения (27) с точностью до двух постоянных интегрирования.
30 Сборник 1835 465
Дифференциальное уравнение (27) для определения радиального перемещения U можно переписать в следующем виде:
Г2 (a2 - f 2аг sin <р + г2 sin2 <р) - г (а2 4- 3аг sin ф 4- 2г2 sin2 ф) ~
(а2 + 2Аг sin ф 4- 2г2 sin2 ф) U - О,
Т. е. в виде линейного однородного дифференциального уравнения с переменными коэффициентами, представляющими собой многочлены степеней г.
|
(33) |
Решение такого дифференциального уравнения может быть представлено в виде обобщенного степенного ряда
U - г1 2 СпГп,
П—0
Где Сп — постоянные, которые могут быть найдены методом неопределенных коэффициентов; X — корни определяющего уравнения, равные для данного уравнения ±1.
|
(32) |
Первое решение дифференциального уравнения при Xl = 1 получается в виде ряда
|
Г Sincp 2 |
|
U, =С |
|
(34) |
Г Sin'Y о
Или
|
Г Sin ф За |
|
Sin ф |
|
21 П=0 |
|
Г/, |
|
С, г |
|
(35) |
Нетрудно заметить, что при 1, как это имеет место в спи
Ральных камерах, ряд, входящий в выражение (35), является биноминальным рядом и суммируется в функцию
(і+^Ф-г)-1. (36)
После подстановки этой функции в выражение (35) получается окончательное выражение для U в замкнутом виде, являющееся первым решением дифференциального уравнения (32), соответствующим корню определяющего уравнение = 1:
И С 3A + 2R sin«p 37
Х а + г sin ф у >
Используя второе значение корня определяющего уравнения = —1, можно получить еще одно решение дифференциального уравнения в виде ряда
|
И |
|
2 |
«
TOC \o "1-3" \h \z CV-^l—^r+^r*-...), (38)
Который также при суммируется и дает второе решение
Уравнения в замкнутом виде
U, - С2 . , ' .—т - • (39)
2 1 г (а -+- г sin ф) '
Это же выражение получается, если воспользоваться для отыскания второго решения из первого формулой Лиувиля.
Подстановка полученных решений в уравнение (32) показывает, что они удовлетворяют исходному дифференциальному уравнению.
Таким образом, общее решение дифференциального уравнения имеет вид
И = Сг За + 2г5іпф г - I - С2 , , ' . , • (40)
1 а + г sin ф 1 i г (a - J - г sin q ) х '
Продифференцировав полученное выражение по г, получим значение производной
DU _ R 2(а г sin ф)2 + а2 р А + 2R Sin ф
~Dr 1 (а + г sin ф)2 2 г2 (а + г sin ф)2 ' ( '
Значения постоянных Сі и С2 можно определить из граничных условий на поверхности оболочки по формулам (30) и (31) с помощью выражения
^Чо-й^ + і'йтЗНї0]- (42)
Получающегося из формулы (23) при подстановке в нее г2 из уравнения (11) и введении обозначения
= Т1+Ю0-2Ц) • (43)
Подставив в выражение (42) значения U из уравнения (40) и производной из уравнения (41), получим выражение для радиальных напряжений в следующем виде:
- (УГ [С>Ф W - Ct-l^t - (а + 2г Sin Ф)] , (44)
Где
Ф (г) За2 -!- 2 (1 + (.1) г sin ф\2а -4- г sin ф). (45)
30* 467
Использование условий на поверхности дает формулы для определения постоянных Cj и С2:
Г - JL __ ________ (а + Q Sin ф)2_______ . , „
^ "= . А + 2Q Sin Ф ф _ ' <4Ь>
Е2 A 4- 2R sin ф ^
С - с R2(P(R)_____ <47)
(1 - 2ц) (а-j-2Я sin ф) '
Где Ф (R) и Ф (е) — значения функции (45) при г R и г = у.
Из структуры формулы (46) вытекает, что при 2R sin ф = —а постоянная Сх обращается в ноль, а значение С2 в формуле (47) становится неопределенным. Если избавиться от. неопределенности, то получим выражение для С2 в следующем виде:
Г =-£- (A -J- Q siN ф)У 2 Е{ (1 — 2ц) (а-і- 2дзіпф) '
Значение угла ф, при котором коэффициент С\ обращается в ноль, для натурных размеров спиральных камер колеблется от —65° до —75°.
Наиболее простой вид формулы для определения постоянных
И С2 имеют для точек, расположенных на вертикальном диаметре поперечного сечения (ф = 0):
Г - р G2 /494
1 Ех 3(R2 — Q2) ' 1
С 11 R*Q*A
E( 1 — 2(A) (RZ-Q2)'
Формулы для определения меридиональных и тангенциальных напряжений можно получить, если представить уравнения (22) и (25) в виде
И ^ МЛ ; (51)
[ r(a-\-1' sin ф) r dr J v 7
Гещіпф Jj + M (52)
1 і a r sin ф • R dr J v
и подставить в них значения U и ее производной из уравнений (40) и (41). Окончательно получим
% = (гг+ТііїПрГ lCl [3а + 2 (1 ^ Г йіп ф1 + С* ; (53) '
А0 (я+• fs'in ф)' [2'U + 3a/"sin(P + ^ІП2Ф) +
+ (За + 2r sin ф) г sin ф] + С2 1 ~:^ sin ф j - (54)
Для точек вертикального диаметра поперечного сечения спиральной камеры формулы значительно упрощаются:
О
|
(55) |
- Р
(56)
(57)
Нетрудно заметить, что выражения (55) и (56) в точности совпадают с формулами Ламе для радиальных и меридиональных напряжений в толстостенном цилиндре. На этом основании можно сделать вывод о том, что введение формул Ламе в решение безмоментной теории тора дает возможность более правильно отразить напряженное состояние толстостенной торообразной оболочки.
Из выражений (49) и (50) видно, что коэффициент С\ учитывает влияние толщины оболочки, а коэффициент С2 — влияние радиуса вращения а оболочки на величину нормальных напряжений.
С помощью полученных формул можно сравнительно просто произвести расчет оболочки в табличной форме.
Рассмотрим пример расчета модели круглой железобетонной спиральной камеры масштаба 1 : 10 применительно к параметрам гидротурбины Красноярской ГЭС. Напряжения вычислим для сечения со следующими расчетными данными: а = 101,0 см; Q = 42,5 см; R = 54,5 см и ц = 0,15. Напряжения будем определять в точках поперечного сечения с величинами углов ф: 90°; 45°; 0°; —30°; —50° и —70°.
Расчет производится в следующем порядке: по формуле (45) находят значения Ф (R) и Ф (е), после чего из выражений (46) и (47) определяют коэффициенты Сх и С2, имея которые по формулам (53) и (54) можно вычислить значения меридиональных и тангенциальных напряжений. Значения функций Ф (R) и Ф (g), коэффициентов Сх и С2 и напряжений аф и о0 для указанных точек поперечного сечения приведены в табл. 1.
|
R: |
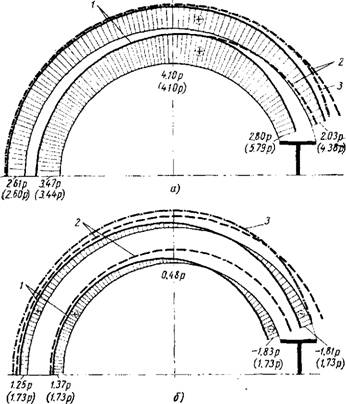
Построенная по результатам расчета эпюра меридиональных напряжений приведена на фиг. 4, а. Для сопоставления полученных значений напряжений (2 — прерывистая линия и ординаты в скобках) показана эпюра, получающаяся при использовании формул Ламе в решении для безмоментной торообразной оболочки (8). Как видно из сопоставления эпюр, они очень близко совпадают во внешней части оболочки до зоны вертикального диаметра. По мере приближения к статору значения напряжений по формуле (8) продолжают увеличиваться, а напряжения, получающиеся по расчету, несколько убывают.
|
Значения функций Ф(1?) и Ф (q), коэффициентов С, и С2 и напряжений
|
На фиг. 4, а приведена также (3 — линия с крестиками) эпюра напряжений на внешней поверхности, найденная экспериментально при испытании в НИИЖБ Госстроя СССР железобетонной модели спиральной камеры. Сопоставление экспериментальной кривой с теоретическими указывает на близкое совпадение их во внешней части оболочки до зоны вертикального диаметра, а в зоне, примыкающей к статору, эпюра экспериментально найденных напряжений сначала близко совпадает с эпюрой, построенной по формуле (8), а по мере приближения к статору начинает убывать, занимая промежуточное положение между двумя теоретическими.
Значения напряжений сгф, найденных экспериментально, в сечениях с углами <р равными 90°; 45°; 0°; —30°; —50°; —70° на внешней поверхности равны соответственно: 2,89р; 2,95р; 3,28р\ 3,60р; 3,75р и 2,83р.
Таким образом, полученное приближенное решение для толстостенного тора во внешней части оболочки довольно точно отражает действительное напряженное состояние в меридиональном направлении, а в зоне, примыкающей к статору, имеет место лишь качественное совпадение, т. е. в обоих случаях наблюдается снижение напряжений у заделки. Определение меридиональных напряжений по формуле (8) дает несколько завышенное значение их в зоне примыкания к статору, что обеспечивает прочность оболочки при большой простоте расчета. 470
Эпюры тангенциальных (торовых) напряжений представлены на фиг. 4, б, где показаны: эпюра (2 — прерывистая линия), получающаяся по существующей методике расчета и эпюра (3 — линия с крестиками) — по результатам эксперимента. Как видно
|
Фиг. 4. Эпюры напряжений: А — меридиональных напряжений; б — тангенциальных напряжений; / — решение для толстостенного тора; 2 — по существующей методике расчета; 3 — по эксперименту. |
Из эпюр, имеет место некоторое совпадение результатов эксперимента с результатами расчета по существующей методике расчета почти во всем поперечном сечении, за исключением околостатор - ной зоны, где в эксперименте наблюдается снижение торовых напряжений и даже перемена их знака в непосредственной близости заделки. Перемена знака тангенциальных напряжений получается также и по полученной формуле (54), однако в более резком виде, так как величины разнозначных напряжений имеют примерно один порядок.
Экспериментальные значения тангенциальных напряжений на внешней поверхности модели в указанных выше точках поперечного сечения равны: 2,13р; 2,20р; 2,56р; 2,Юр; 0,93р и —0,1р.
Таким образом, для определения тангенциальных напряжений в спиральных камерах с достаточным приближением можно воспользоваться формулой (5) существующей методики расчета спиральных камер как безмоментных торообразных оболочек. При этом следует учитывать возможность появления напряжений противоположного знака в околостаторной зоне. То, что тангенциальные напряжения, найденные теоретически, довольно существенно отличаются от экспериментальных, является следствием принятых допущений в расчете.