ПРИМЕНЕНИЕ ЖЕЛЕЗОБЕТОНА МАШИНОСТРОЕНИИ
Существующая методика расчета металлических спиральных Камер
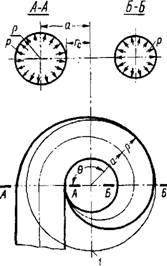
Спиральная камера представляет собой неправильную торообразную оболочку. Расчет такой оболочки является сложной математической задачей, отыскание точного решения которой в настоящее время весьма затруднительно и вряд ли целесообразно. Поэтому при решении ее в качестве расчетной схемы (фиг. 1) принимается для каждого сечения торообразная оболочка, находящаяся под действием внутреннего давления, интенсивностью р кГ/см2.
Металлические спиральные камеры рассчитываются с помощью простых формул, получающихся главным образом на основе использования зависимостей безмоментной теории оболочек вращения. При этом меридиональные напряжения огф торообразной оболочки толщиной T И радиусом поперечного сечения Q Выражаются через напряжения сг° =
Рр u Фиг. 1. Расчетная схема спираль-
„ігп ^„,/nf, ной камеры:
|
|
|
У- для тонкой цилиндрической оболочки по «котельной» формуле путем умножения их на коэффициент К, Учитывающий отличие напряженного состояния тора от напря женного состояния цилиндра: |
/ — контур тора, заменяющего спираль в расчетной схеме.
|
OlK. |
|
(1) |
Для круглых сечений
Sin Ф
|
(2) |
1 + ~ sin ф
Где а — расстояние от оси вращения до центра поперечного сечения тора;
Ф — угол, отсчитываемый от вертикального диаметра поперечного сечения тора и считающийся положительным в направлении от статора к внешней части тора.
Напряжения в местах заделки звеньев спиральной камеры в статор определяются с помощью коэффициента К — Кх, полученного приближенным решением по моментной теории
|
3 |
|
(3) |
(1 — Ц)— \L-J-
Где гс — расстояние от оси вращения до места заделки спирали в статор; р, — коэффициент Пуассона.
Для металлических спиральных камер (jx = 0,3) значение коэффициента Кх определяется формулой
Кг = 1,135 + 0,228—. (4)
Ї С
Тангенциальные напряжения о9 на основе безмоментной теории тонких торообразных оболочек получаются постоянными по величине и равными соответствующим напряжениям в цилиндрической оболочке:
TOC \o "1-3" \h \z _ 1 О _____ 1 PQ ,гч
— ~2~ аФ ~ ~~2~ ' T ' V '
В случае значительной толщины оболочки спиральной камеры в выражения для коэффициента К вводится уточненное значение радиуса
Е'=е + 4"- (6)
Указанными формулами можно пользоваться также и для приближенной оценки напряженного состояния железобетонных спиральных камер круглого сечения. Однако следует иметь в виду, что при значительной толщине оболочки будет иметь место вне - центренное растяжение, т. е. напряжения по толщине оболочки будут распределяться неравномерно. Поэтому уточнение расчета необходимо провести, в первую очередь, в направлении более точного учета влияния толщины оболочки на распределение напряжений.