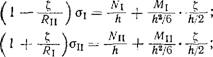ПРИМЕНЕНИЕ ЖЕЛЕЗОБЕТОНА МАШИНОСТРОЕНИИ

Статика оболочки средней толщины

Рейсснер Э. показывает, что для предложенной им теории, учитывающей члены порядка h/R по сравнению с единицей, к шести уравнениям равновесия тонких оболочек [2] необходимо добавить седьмое уравнение, являющееся вторым недифферен­циальным уравнением в системе статических уравнений равнове­сия упругих оболочек [11].

Для оболочки, отнесенной к ортогональным координатам, уравнения статики в этом случае будут иметь вид [11], [12]:

П. Nu + N22 + Nn +

Dh 12 ^ dl* 22 ' egi 21 dl:

+ + 0; \ A] 2 K22 /

N,% + iV2

+ тїг^) + + = 0;

^"п + ^ + ^-^ЛІ,,- (20) — ai^Qj = 0;

— a ^Qz 0;

K22 K]2

VII. M12-M21 = ^[(^---±-)(N12 + + N21) + ^-(N11~N22)];

#+ = 1 - f — _i_\ ;

2 ( ' R22 ) '

Их ~ А; а2 = В; ^ = а; = р.

Q+ и — значения внешней нагрузки на обеих (верхней и нижней) поверхностях оболочки.

В этих уравнениях принято, что тангенциальные составляю­щие нагрузки отсутствуют, т. е. q+ и q~ — нормальны к поверх­

Ностям оболочки. Отсутствует также внешняя моментная нагрузка. Собственный вес оболочки не учитывается. Правило знаков по­казано на фиг. 3.

Чтобы получить соотношения между напряжениями и дефор­мациями, нужно повторить ход рассуждений Рейсснера Э., поскольку он не учитывал внешней нагрузки в предложенных им приближенных формулах, связывающих усилия и моменты с напряжениями. Такой учет сделал Нахди П. [12] и получил следующие формулы:

(21)

2 Ft L \ /1/2 / J ' 2 ft L V A/2 / J '

ШП S — (Я + ж) ■

Эти формулы даны для координат, ной системы (|ь £), в [кото­рой линии ^ = const И in = const — есть линии кривизны-средин­ной поверхности, а £ — координата по нормали к срединной поверхности.

Отправляясь от системы уравнений (20), через частные про­изводные потенциальной энергии деформации, относящейся к слою, окружающему срединную поверхность и имеющему толщину

2£ < h, где ■—y < £ < + по соответствующим силам и мо­ментам можно получить искомые соотношения. Для этого в вы­ражении потенциальной энергии деформации [1], [11]

ХО+^Н' + ЖгИ

Нужно заменить напряжения через их значения по формулам (21). В формуле (22) коэффициент Пуассона принят равным нулю [8]. Кроме того, здесь обозначено х, = т1£; ти = т11£

И 0 = 0?.

После соответствующих выкладок получим: для той части потенциальной энергии деформации, которая обусловлена напряжениями оь он и т^ ц, параллельными средин­ной поверхности,

М\ + Mii + +

(23)

Для той части энергии деформации, которая обусловлена по­перечным сдвигом,

Qj + Qh.

1 * 5 ' 2Gh '

Для части энергии деформации, обусловленной нормальным напряжением о и нагрузкой q+ и q~

JL

70 Е

Пп = [ 1 з (qr (НГ + 13 (q-)HH-Y + 9q+q-

-^[{q+m + q-H-)S\. (25)

Переход от координатной системы £) и соответствую­

Щих ей усилий и моментов к координатной системе £2, Q и соответствующим усилиям и моментам совершается при помощи зависимостей дифференциальной геометрии

0 =

И соотношений [9]

Nj = Nn cos2 ф + N22 sin2 ф + (N12 + N21) sin ф cos ф; Nlt її = (N22 — jVh) sin ф cos ф + N12 cos2 ф — N21 sin2 ф; A^ii, і = (N22 — Nn) sin ф cos ф — Nl2 sin2 ф + N21 cos2 ф; Nn = Nu sin2 ф - f N22 cos2 ф — {n12 + N31) sin ф cos ф; Qi = Qi cos ф — Q2 sin ф; Qn = Qi sin ф + Q2cos ф.

Формулы для моментов имеют тот же вид, что и формулы для сил; ф — угол между направлениями линий ^ и Подставив уравнения (26) и (27) в формулы (23) — (25), получим

Nn + N222 +~(Ni2+N2d] +

< ~~ 2Eh

+ Ш? И + ^ + 4" (М12 + мл)2] + І [ht - і) X

X (N22M22~ NuMu) + ~ (Nn + N22) (M12 + M21) +

A12

-і - ~ (Mil + M22) (N12 + NaS] ; (28)

6 +

Формулы (28) и (29) необходимо совпадают с формулами Рейсснера Э. Автор работы [11] допускает при использовании

447

Формул для напряжений о, Ті и Тц пренебрежение членами по­рядка h/R по сравнению с единицей, вследствие малости этих напряжений. Эт. о правило было использовано при получении формул (25) и (29).

Потенциальная энергия деформации выражается суммой фор­мул (25), (28) и (29)

Я = nt + П, + Пп. (30)

Таким образом, получаем

= жгг =- ж + ж [ (ж: - тЬ)Ml1 +

^ (М12 + Мп)] ;

822 - 2 + ж [(ж ~~ ж)м*2

+ (М12 + Л421)] ; ДП дП_ 1 /А, , ,, ч, 1

/аі

К12

TOC \o "1-3" \h \z v - ЛШ - - JL._Јi_. v ПП

Vl ~ dQj ~ 5 Gh ' — ЛО - ~~ R Gft '

_ дП _ 12 .. 1

Xl1 ~ ЖГ - + "Ж

+ -^-(л/12 + Л/21)];

Л22 ~ Ж^Г — ЖiKJa2 Ж

= = Ж7 = W = і + +

Решение системы уравнений (31) относительно сил и моментов дает нам обратную зависимость, необходимую для приведения системы статических уравнений равновесия оболочки I—VII к конкретной задаче равновесия оболочки спиральной камеры, если иметь выражения компонентов деформации и изменений кривизны еп; е22; є12 = є21; х^; х22; xJ2 = х21 через линейные перемещения ы1; ы2; w и угловые перемещения ^ и срединной поверхности. 448

І'де w' и w" —дополнительные Компоненты поперечной нормаль­ной деформации. Для них Нахди П. [12] дает формулы

[4-«+т( + І

2 Т 9

Eh

Для координатной системы в линиях кривизны.

При переходе к общим ортогональным координатам величины Н+ и Н~ не меняются. Если величинами S и Т пренебречь, то формулы (36) получат вид

— ^H^q'H-)- 2

(q+H++q'H-).

W + if = W <Я+)2 + 26?~ (Я_)2 +

V + 9 q -

Пиях Главной кривизны (положив коэффициент Пуассона равным нулю):

Ni = EhEj; Л/и -— ЕЫ2,

Eh ( , /і2 \ П т-(е12+j;

ДГ £/г j, /г2 \ (40)

Eh3 Eh3 £7г3

Ml = -72" M]I = ~ТГ " ^ M»> і ^ І2"Хі2-

Видно, что для совпадения системы формул (39) с системой (40) необходимо, кроме перехода от обобщенных ортогональных координат к координатам в линиях кривизны, пренебречь чле­нами порядка h/R по сравнению с единицей. Несовпадение формул для касательных усилий N12 (21) объясняется существованием для оболочки средней толщины в системе уравнений статики дополнительного уравнения VII.