ПРИМЕНЕНИЕ ЖЕЛЕЗОБЕТОНА МАШИНОСТРОЕНИИ
Геометрия спиральной камеры
Геометрия спиральной камеры определяется следующим образом. Радиус входного отверстия спиральной камеры q находится по заданной входной скорости воды. В зависимости от него по формуле
|
2л — і С |
|
(1) |
|
2 га |
— Vr2+ t2
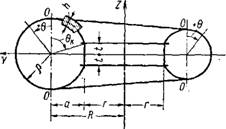
Строится поперечное сечение спиральной камеры (фиг. 1). Здесь С — величина, зависящая от полного расхода воды через турбину; г — радиус статорного
Кольца; t — половина высоты статорного кольца.
Так как формула (1) сложна для введения ее в уравнения статики, то Корнецкий А. Л. аппроксимирует ее следующим путем. Принимается, что для определенной по этой формуле спирали, лежащей в плоскости XOY,
9 = Qx (1 — т, (2)
Где q, — радиус входного отверстия (начальный ®иг - ^ Геометрия спиральной камеры.
Радиус).
Для р = л коэффициент аппроксимации k -=
В большинстве конструкций; здесь QK —
|
|
Угол Р >• л в рассмотрение не принимается ввиду того, что за его пределами кольцевое сечение спиральной камеры быстро переходит в эллиптическое, принимаемое из конструктивных соображений; здесь напряженное состояние не интересно, так как действующие в этом месте усилия малы, поскольку при постоянной толщине оболочки радиус q сильно уменьшается. В работе Корнецкого А. Л. показано, что построенная по формуле (2) спираль очень мало отличается от гидравлической, но вносит весьма существенные упрощения в расчет.
В принятой системе координат уравнения поверхности будут х = (г + а + Q sin 0) sin р; у = (г + а + Q sin 0)cos р; (3)
Z = qcos 0.
Линии 0 = const и р = const являются криволинейными координатами на срединной поверхности оболочки. Выражение
TOC \o "1-3" \h \z Дх дх. ду ду. Dz Dz ______________________ да,
Указывает на то, что данные координаты не ортогональны. Отыщем ортогональные координаты из условия
Дх дх. ду ду. Dz Dz _ „ ...
Ж' Ж + Ж ф + Ж' ар ~ ' ^
Положив
E=M«, Р); Q=MP) и а = /з(Р).
Дифференцируя уравнение (3) по а и р и подставляя в формулу (4), получим
|
Откуда примем тогда Где |
Іfpzrr* + = (5)
, . . 1 + sin 6 /СЧ
G = (Q + «) Г. й • (6)
Cos 0 t
С = — а
Cos 0
А = —є - j—;—: , (7)
1 + sin0 4 '
0<є = —<1. (8)
^ q + a ^ w
Формулой (7) определяются преобразования
2ea
Cos 0
E2 + a2 '
. Q є2 — a2
Sin 0 =
E2 + a2
Уравнения поверхности, отнесенные к ортогональной системе координат, принимают вид
Х = F (а, р) sin р;
У = F (а, р) cos Р; ^
2ва
6 в2 + а2 '
Cos 8
Таким образом, рассматриваемая область оболочки ограничивается пределами 1) 0 < р < я;
[ а = 0 — плоская спиральная кривая;
|
—а. |
|
Где |
|
F(a, Р) |
|
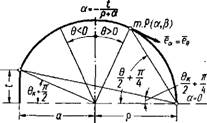
R + a + ei^qr^ Геометрический смысл а виден из фиг. 2. |
^ і а = —1 — полуокружность.
|
Фиг. 2. Геометрический смысл координаты а. |
|
2qb |
Для полученных координат по обычным формулам дифференциальной геометрии [5] вычисляются радиусы кривизны вдоль координатных линий а и р и коэффициенты Ламе (А я В).
А =
Є2 + <х2
=-F-(l + sin 0)
В = F]/l + k2(Bx/F)2, (12)
Где
Вх = ei(l + - J - sin 6 ) и F — F (а, p);
K2 ■
Sin 0
R* 2 F ll+k^BJF)* _ £ TQx COS 0 1
-(- K2 (BJFf
R12
|
(13) (14) (15) |
|
Ei |
|
AF2 |
В формуле (14)
Так как =f= О, то линии a ~ const и p = const не являются
К12
Главными линиями кривизны.
Полученные выражения легко упрощаются за счет отбрасывания пренебрежимо малых членов, содержащих величину k2. Тогда имеем
S = Т7 = г - f a + q sin Є = ^ (1 + Я sin 0), (16)
Где R = г + а и % = q/R\
Ru Q ' 1 sin 6 sin в
(18)
R22 F ^(l + XsinG) '
1 rQ) cos6 .
Rlt aR* (1 + X sin9)2'