ПРИМЕНЕНИЕ ЖЕЛЕЗОБЕТОНА МАШИНОСТРОЕНИИ
ЭКСПЕРИМЕНТАЛЬНЫЕ И ТЕОРЕТИЧЕСКИЕ ИССЛЕДОВАНИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ ПОЛУДИСКА
Конструкции в виде полудисков могут применяться в различных областях строительства, в частности, в прессостроении, где диски различных очертаний могут использоваться как ригели железобетонных предварительно напряженных станин.
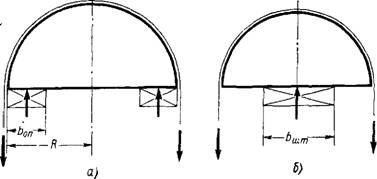
Ригель пресса находится в сложных условиях работы на знакопеременные многократно повторные нагрузки. В одном случае это нагрузка от действия предварительно напряженной арматуры (оплетки), (фиг. 1, а), в другом — эксплуатационная нагрузка (фиг. 1, б).
Форма ригеля может быть самой разнообразной, в зависимости от внешних нагрузок, расположения предварительно напряженной арматуры и других факторов. Поэтому желательно подобрать такую форму, при которой от внешних нагрузок ригель работает наиболее рационально. Одной из таких форм может быть полукруглый диск.
Полукруглая форма проста в изготовлении, имеет преимущества в расчетном отношении, так как хорошо вписывается в полярную систему координат, что дает возможность получить сравнительно простой расчет. Применение дисков (в частности, кругового очертания) с внешней предварительно напряженной арматурой в виде оплетки в качестве ригелей для прессов в условиях работы на многократные нагрузки позволяет эффективно использовать работу бетона и арматуры. Во-первых, потому что в диске от оплетки создается двухосное напряженное состояние, так как кроме вертикальной нагрузки еще действует горизонтальное боковое обжатие, уменьшающее растягивающие напряжения. Во-вторых, потому что это позволяет применять в качестве оплетки высокопрочную проволоку и канаты, имеющие высокие расчетные характеристики.
Полукруглая форма позволяет равномерно и плавно распределить по всей ее криволинейной поверхности давление от оп - 340 летки, не вызывая в арматуре концентраций напряжений (что, например, имеет место в углах прямоугольных и трапецеидальных форм дисков) и создавая тем самым благоприятные условия для работы арматуры и бетона, при многократных нагрузках. Конструкции прессов с дисками полукруглой формы нашли свое применение в вертикальном прессе усилием 120 m и в проекте горизонтального пресса усилием 50 ООО т для изготовления труб (см. статью Людковского И. Г.).
В настоящее время данных по методике расчета таких конструкций, а также данных исследований, хотя бы на действие
|
Фиг. 1. Схемы загружения: А — нагрузки от действия предварительно напряженной арматуры (оплетки); б — эксплуатационная нагрузка. |
Статической нагрузки, почти нет. В связи с тем, что ряд практически важных вопросов не мог бы быть решен теоретически, необходимо было провести экспериментальные исследования. Целью экспериментальных исследований было выявление напряженного состояния дисков как элементов ригелей прессов и получение исходного материала для разработки метода расчета.
Основными вопросами, которые необходимо было решить экспериментально, были:
1. Исследование напряженного состояния диска полукруглой формы при двух видах загружения.
2. Влияние на напряженное состояние диска расположения и размеров подштамповых плит.
3. Распределение давления в диске под опорами и штампом.
4. Распределение давления по криволинейной поверхности диска от внешней арматуры (оплетки) с учетом и без учета трения.
5. Изучение форм разрушения при двух схемах загружения.
Методика эксперимента была разработана так, что отражала
Работу дисков как плоских элементов в реальном прессе. Испытания проводились на моделях, состоящих из двух бетонных дисков
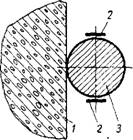
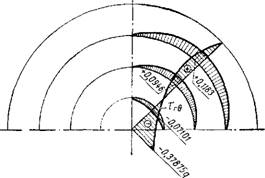
(без арматуры) полукруглого очертания и облегающей их криволинейную поверхность оплетки (фиг. 2). Диаметр полудиска равнялся 100 см, толщина 25 см. Такое значение толщины было принято для того, чтобы исключить потерю устойчивости плоских элементов и модели в целом. При этих соотношениях пролета и толщины имеет место плоско-напряженное состояние. Оплетка
Состояла из одного слоя вы - і сокопрочной проволоки периодического профиля диаметром 5 мм; число проволочек в слое 30 шт. Для уменьшения трения между бетоном дисков и арматурой оплетки была проложена металличе - | екая прокладка из кровель - I ной стали толщиной 1 мм. Испытания проводились при двух видах загружения, один из которых соответствует работе дисков после окончания предварительного натяжения внешней арма - s туры (оплётки) или моменту і передачи нагрузки на колонны станины при натяжении і самим прессом (см. фиг. 1, а). j Величина опор составляла,
I как это должно было быть j в реальном прессе, 0,47? = j =20 см, где R — радиус
Полукруглого диска. | Другой вид соответство - ' вал работе ригеля реального пресса ТЖ-600 при эксплуатационной нагрузке, а также работе дисков ригеля станины при натяжении внешней арматуры самим прессом (фиг. 1, б).
Величина штампа прилагаемой нагрузки была принята применительно к размерам опирания цилиндра пресса ТЖ-600 и составляла 0,8R = 40 см.
Для измерения деформаций использовались тензодатчики с базой 50 см. Датчики располагались на обеих сторонах дисков в двух системах координат (прямоугольной и полярной) с тем условием, чтобы в наиболее важных сечениях показания датчиков дублировались. Для уменьшения влияния местных напряжений по контуру диска на показания датчиков ось вертикального и горизонтального датчиков располагалась на расстоянии 5 см от 342
края диска. Модели дисков при испытаниях находились в вертикальном положении. Первоначально верхний диск с заранее заготовленной оплеткой из высокопрочной проволоки подвешивался на балки. Затем на пояс оплетки ставился нижний диск и вся подвижная система закреплялась монтажными болтами в своей плоскости (см. фиг. 2), после чего производилось испытание на один из видов загружения. После тщательной выверки правильного положения дисков, расположения штампов и домкрата ослаблялись монтажные болты и давалась нагрузка домкратом для натяжения оплетки. Эта нагрузка принималась в дальнейшем при снятии отсчетов за нулевую. Надо сказать, что модель представляла собой подвижную систему. Поэтому, если имелся небольшой перекос положения дисков в плоскости модели, то при увеличении давления он исчезал за счет того, что диск имел возможность скользить в оплетке вокруг своего полюса. Тщательная выверка положения домкрата и опор исключала возникновение горизонтальных сил в модели, что могло повлиять в известной степени на смещение опор. Для плавного распределения давления и уменьшения величины трения под опорами в последних ставились асбестовые прокладки.
Предварительные испытания модели сразу же при двух видах загружения позволили выявить момент появления трещин. Поэтому в дальнейшем испытания проводились только в стадии работы дисков до появления трещин.
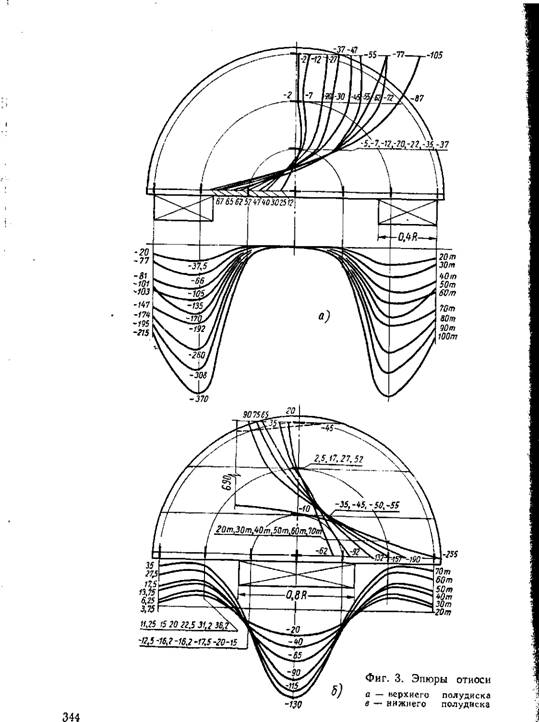
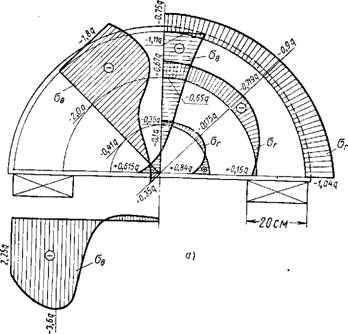
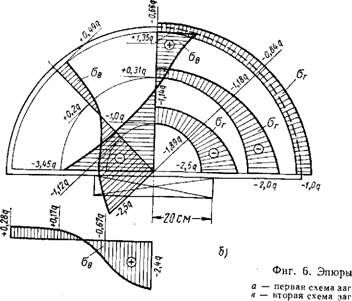
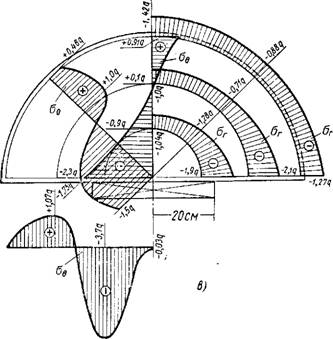
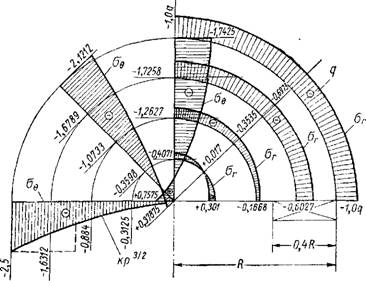
Нагрузка давалась ступенями через Ют до 100 т при первой и до 70 т при второй схемах загружения. Испытания проводились сначала при первом виде загружения, затем нагрузка менялась и при втором виде испытания проводилась до появления трещин. Затем нагрузка снова менялась и определялся момент появления трещин уже при первом виде загружения. Эпюры относительных деформаций бетона марки «500», полученные при двух видах загружения дисков, показаны на фиг. 3, а—в.
На фиг. З, а—в показаны симметричные, относительно вертикальной оси эпюры. На самом деле они симметричными не получаются из-за многих возможных факторов, таких как неправильное расположение опор, домкрата, неоднородность материала диска и др. Принятая методика эксперимента эти факторы учла и позволила дублировать показание каждого датчика в точке от 2 до 4 раз. Исходя из этого, стало возможным вывести средние данные и сравнить с теоретическими. На эпюрах показаны горизонтальные деформации в среднем радиальном сечении диска, а также вертикальные деформации под опорами и штампом при различных нагрузках от условного нуля (10 т) до 100 т при первом идо 70 т при втором видах загружения. Величины относительных деформаций показаны на фигурах увеличенными в 10е раз. Для наглядности эпюры вертикальных деформаций под опорами и штампом вынесены за границы полудиска. Как видно из фиг. 3, 6-е, при второй
|
|
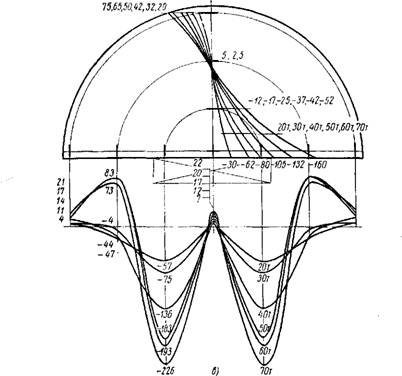
Схеме загружения при ширине штампа 0,8R эпюры деформаций различаются между собой, особенно под штампом. Это обстоятельство объясняется тем фактором, что характер распределения давления в диске под штампом, а также величина напряжений зависят при одной ширине штампа от его жесткости.
Для верхнего ригеля использовался менее жесткий штамп, что ускорило момент появления радиальной трещины. На характер распределения давления при втором виде загружения особенно влияет трение под штампом, которое увеличивается по мере увеличения размеров штампа и зависит от его жесткости. Для уменьшения трения под штампом были положены асбестовые прокладки, но этим трение полностью не могло быть исключено и в какой-то степени имело место и наложило отпечаток на напряженное состояние полудисков, особенно при втором виде нагружения.
|
Тельных деформаций бетона: (увеличено в 10е); б — верхнего полуднска {вторая схема загружения); (вторая схема загружения), |
Другим не менее важным фактором, влияющим на напряженное состояние дисков, является трение под оплеткой.
|
|
Фиг. 4. Расположение датчиков:
|
Прежде всего было необходимо выяснить, как распределяется давление от оплетки по криволинейному контуру диска при нали- |
|
0,6 Пр. |
|
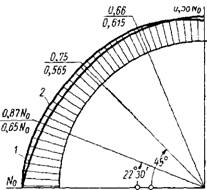
Фиг. 5. Эпюры изменения усилия в проволоке в зависимости от полярного угла в полукруглом диске при действии силы трения: |
|
/ — экспериментально; 2 — теоретически; N о — усилие домкрата. |
А — на оплетке; б — иа одиночной проволоке; 1 — бетон; 2 — датчики; 3 — проволока.
Чии сил трения. О характере распределения давления можно было узнать по деформациям оплетки в разных точках криволинейного контура диска. Поэтому, кроме датчиков на бетоне, были наклеены датчики на проволоке оплетки. Кроме того, были проведены дополнительные испытания модели, которая представляла собой конструкцию из двух бетонных дисков, стянутых проволокой диаметром 5 мм из стали марки Ст. 5. Между проволокой и бетоном были проложены листы оцинкованной стали толщиной I мм.
|
А) |
Дополнительные испытания были вызваны тем, что на проволоку оплетки можно было наклеивать датчики только с внешней стороны (фиг. 4, а). Это могло привести к известным погрешностям, так как на деформации растяжения проволоки накладывали отпечаток деформации изгиба, особенно в углах
диска. При испытании с одной проволокой датчики могли наклеиваться по оси проволоки с двух сторон (фиг. 4, б) и это исключало деформации изгиба в показаниях датчиков.
Качественная картина получалась одинаковая в обоих случаях, но деформации в первом случае (фиг. 4, а) были несколько большими из-за влияния изгиба.
Испытания с проволокой показали, что давление от оплетки по криволинейной поверхности полудиска можно принять изменяющимся по закону (фиг. 5)
Здесь N0 — усилие домкрата;
IVe — усилие по длине проволоки в зависимости от полярного угла;
0 — полярная координата;
(lx — коэффициент, равный 0,35 при трении проволоки по кровельной стали.
После того как решен вопрос о распределении давления по контуру диска, становится ясным, что при первом виде загружения трение уменьшает сжатие по криволинейному контуру диска. Поэтому для первого вида загружения худшим будет тот случай, когда диск загружен по контуру равномерно распределенной нагрузкой без трения.
При втором виде загружения трение ухудшает работу ригеля, вызывая дополнительные растягивающие и сжимающие напряжения. Вообще трение неблагоприятно влияет на работу арматуры и бетона, поэтому возникает вопрос о способах его устранения. Уменьшить трение можно, применив в качестве оплетки гладкую проволоку, смазанные металлические прокладки, а также вибрацию. Примером работы дисков на равномерную нагрузку без трения приближенно можно считать работу дисков при намотке внешней арматуры на поворотном столе ДН-5 или на машине ДН-7.
На фиг. 6, а—в показаны эпюры напряжений в диске при двух видах загружения, при совместном действии сил трения и нормальных сил от оплетки по криволинейному контуру. Надо отметить, что при переходе от деформаций к напряжениям использовался постоянный модуль упругости на сжатие, полученный экспериментально при испытании призм 20 X 20 X 80 и кубов размерами 20 X 20 X 20 см. Вообще говоря, это не совсем правильно, так как модуль упругости зависит от стадии работы материала и это накладывает свой отпечаток погрешности, особенно в тех зонах, где напряжения могут менять знак. Однако, учитывая то, что диски испытывались в стадии работы до появления трещин и модуль упруго-пластичности при растяжении меньше, чем при
|
|
|
|
Щ
Сжатии, вследствие чего отклонения могут быть только в меньшую сторону, приближенно сочли возможным пользоваться постоянным модулем упругости при сжатии. Таким образом, удалось сравнить эпюры экспериментальных напряжений с теоретическими.
Величины напряжений на фиг. 6, а—в выражены в общем случае в долях от q:
Ч = Ж' ®
Где N — усилие домкрата;
R — радиус полудиска.
|
Ружения, Р= 1 00 т; б — вторая схема загружения, верхний ригель, Р = 60 т\ ружения, нижний ригель, жесткий штамп, Р — 60 т. |
|
Напряжений: |
Несмотря на то, что краевые датчики были несколько удалены от контура диска, все же сказывалось влияние контактных напряжений на показания датчиков. Поэтому наиболее правильными можно считать показания датчиков, расположенных внутри контура диска, и тем вернее, чем дальше от контура. При вычислении
нормальных напряжений на криволинейном контуре диска в расчет принималась «условно-средняя» толщина диска, равная 20 см, при «фактической толщине», равной 25 см и ширине размещения оплетки, равной 15 см. Проверка равновесия экспериментальных эпюр показала, что равновесие соблюдается в пределах 4—16%.
Кроме того, были также проведены испытания дисков при первом виде загружения без влияния сил трения. Нагрузку без трения можно создавать в дисках, как было отмечено выше, при намотке на поворотном столе ДН-5 (фиг. 7). Модель состояла из
|
Фиг. 7. Модель после намотки на поворотном столе ДН-5. |
Двух бетонных дисков и двух стоек. Ширина опоры составляла 0,4^. В качестве оплетки использовалась гладкая высокопрочная проволока диаметром 4 мм. Усилие в проволоке — 1000 кГ. Оплетка на модель навивалась в виде двух слоев. Число проволочек в первом слое — 50 шт., во втором от 30 до 40 шт. Датчики были расположены в среднем радиальном сечении и под стойками. Показания датчиков снимались после намотки целого слоя. Здесь надо отметить, что при намотке модели большое влияние могли оказать горизонтальные силы, которые могли вызвать смещение опор, что крайне нежелательно, Чтобы это избежать, модель при сборке скреплялась металлическим поясом в своей плоскости. Металлический пояс поднимался по мере навивки проволоки на модель и затем совсем убирался. Принятые меры полностью исключали возможность смещения опор вследствие действия значительных горизонтальных сил в плоскости модели. Эпюра напряжений, полученная при первом виде загружения от нагрузки без влияния трения, показана на фиг. 11 (IV) при Р — 100 т (1 слой), где Р — усилие предварительного натяжения оплетки.
Одним из важнейших вопросов, касающихся работы ригеля, является вопрос трещиностойкости. Очень важно, чтобы при знакопеременных нагрузках в диске не возникли трещины от больших растягивающих напряжений. При испытании наблюдался момент появления трещин при обоих видах загружения, а также некоторые намечающиеся формы разрушения, хотя до разрушения диски не доводились из-за возможной потери устойчивости модели. При первом виде загружения была замечена лишь одна намечающаяся форма разрушения от больших растягивающих напряжений в пролете. Скалывания или среза углов диска в опорных сечениях не наблюдалось. При втором виде (нагрузка в середине пролета) замечены две возможные схемы разрушения. Первая — от больших растягивающих напряжений в крайнем волокне среднего радиального сечения, приводящих к появлению радиальной трещины. Такая намечающаяся схема разрушения возможна при ширине штампа
Ьшт <
Вторая форма разрушения от скалывания углов возможна при ширине штампа
Ьиїт ^> R-
При первом виде загружения от совместного действия сил трения и нормального давления при ширине штампа 0,4/? = 20 см трещина появилась при 130 и 100 т от равнсмерно распределенной нагрузки без влияния трения (фиг. 8, а и б). При втором виде при действии трения и нормального давления оплетки при ширине штампа 0,8R = 40 см трещина появилась уже при 70 т (фиг. 8, в).
Для разработки метода расчета конструкций с дисками полукруглой формы были проведены теоретические исследования. Эти исследования представляют собой продолжение работ, начатых канд. техн. наук Хлебным Я. Ф. Задача решгется вариационным методом. Критерием для наилучшего приближения компонентов напряжений к их истинным значениям служит принцип Ка - стильяно, выражающий в энергетической форме принцип кинематики о неразрывности деформаций. Аппроксимируя искомую функцию рядом, мы должны считать наилучшим такое приближение, которому отвечает условие
Эвн = Гпіп, (3)
Где Эт — выражение внутренней энергии системы.
Функцию напряжений представим в виде двух слагаемых
П
9) ~= ^Ок (Г, 9) Jr 2аЛ< (г. 9)' (4)
Фиг. 8. Образование трещин в диске:
" ~ лрн пеРвой схеме загружения при действии нормального давления от оплетки и сил трения; б - при первой схеме загружения прн намотке на поворотном столе ДН-5, в-при второй схеме загружения при действии нормального давления от оплетки н сил трения.
Каждое из которых принимаем в таком виде:
|
= R Ф • 4 к /с' = R Ф.. ЧО I я |
|
(5) (6) |
|
' Ок (г, в) F Of (г, в) |
Параметр а{ находится из условия
ДЭвн
О (і = 1,2., .),
Да-і
Где F,
Ок (г 9) отвечает граничным условиям; ^оі(г-в) дает нулевые значения на контуре. Подставляя аппроксимирующую функцию (4) в уравнение равновесия плоской задачи и вводя безразмерную координату £> =
== ~ (где 0 < е < 1; R — радиус полудиска; г — переменный к
Радиус), получаем в общем виде выражения для напряжений в полярных координатах-.
Где а*, of, — напряжения, выраженные через функцию (5); a°r> °e> x% — напряжения, выраженные через функцию (6).
Функцию (5) можно задать. в виде полинома, тригонометрического ряда или в сочетании их. В статье Я - Ф. Хлебного «Применение вариационных методов к расчету элементов конструкций прессов» для решения этой задачи применялись полиномы. Для случая нагружения диска равномерно распределенной нагрузкой по криволинейному контуру функция напряжений (6) была принята
. Foi (q, 0) = RomФоп = (1 - Є)УОТ (а - ф)У" . . ., где (10) для полудиска:
А = It; 0 < ф < я; т, п = 1, 2, 3, . . .
23 Сборник 1835 353
Однако для получения правильной картины распределения напряжений в диске, решение нуждается в уточнении введением дополнительных членов аппроксимирующего ряда. Теоретические и экспериментальные исследования показали, что при решении задачи в полиномах можно улучшить предыдущие решения уже
|
2,3525 2,5379 |
X 2,2929 Г) Щ Zom |
\ 1.9007 |
|
|
=QF====j 1,3255 |
|||
|
2Л035 |
U Щ 1,9901 / 1,6260 |
J 1,1009 |
|
|
1,6853 |
/ 0,9862 |
------- І |
|
|
1,1668 |
X 1,2716 |
0,8606 |
J |
|
0.4029 |
0,6571 |
==/ 0,5592 |
-j |
|
%2688 0,0539 |
^ 0,1940 |
||
|
0,6870 |
0,7083 |
0,7375 1,0842 0,0 |
|
|
0,6525 |
0,9964 |
||
|
0,0 |
0,0 4= |
|
А) |
|
5) |
|
Фиг. 9. Изменение эпюры сгв в зависимости от вида аппроксимирующей функции а — при t = 1; б — при t = 2; в — при t = 4. |
При одном первом члене аппроксимирующего ряда, если принять функцию в виде
^ <„..) = (L-e^)Vm(*-cp)Vn..-> (11)
Где t, т, п = 1, 2, 3, . . .
Если для сравнения выбрать за критерий тангенциальные напряжения по среднему радиальному сечению, то наиболее близка по своему характеру к экспериментальной оказывается эпюра <г9, полученная с функцией (11) при t = 4 (фиг. 9, в). Изменение
Эпюры о9 при 8 = - у - в зависимости от Roi показано на фиг. 9, а—в,
Где угол 8 отсчитывается от горизонтальной оси.
Однако, как видно из фигур, все еще неясным остается вопрос о величине напряжений в полюсе полярной системы. Дополнительные члены ряда уточняют предыдущие решения, но в полюсе по-прежнему дают нулевые значения для напряжений. Этого можно избежать, если для решения задачи функцию напряжений принять в виде
FonО, 9) = ЯотФоп--= (1 - e')Ym(l -2lQn) Silft. . ., (12)
Где t, т, п = 1, 2, 3, ...;/ = О, 1, 2.
354
Уже при первом члене при t, tn = 1 I = 0, т. е. при
Fono. e) = (l-e)2e2sm26 ... (13)
Удалось получить в полюсе полярной системы для напряжений конечную величину. Тогда напряженное состояние полудиска при равномерно распределенной нагрузке по его криволинейной части и нагрузке, распределенной по произвольному закону по прямолинейной части, описывается формулами:
-- ^F - I- ai f О - 2q є2) 2 cos 20 - i -
TOC \o "1-3" \h \z 2 (1 — 3q -4- 2q2) sin20]J; (14)
- {-^r ЯЖ + «і (2 - 12Є + 12e2)sin2 в}; (15)
Tre---: --^-fliO -4e-r3ea)sin20... (16)
При распределении нагрузки по прямолинейному контуру диска по закону
</2(0) =
Где k — коэффициент, определяемый из условия равновесия, напряженное состояние полудиска при одном первом члене ряда описывается - формулами:
Ar - q {— е*+ 0,3787 [2 (1 — 2q + q2) cos 20 ;
+ 2 (1 — 3q + 2q2) sin2 0)1; (17)
(7e =--q [— 2,5ev' f 0,3787(2 — 12q + 12e2)sin20], (18)
= —<7-0,3787 (1 — 4q + 3q2) sin 20, (19)
Где q — равномерно распределенная нагрузка по криволинейному контуру диска. Эпюры напряжений показаны на фиг. 10. Можно применить еще один способ решения задачи с использованием элементарного решения для простой балки с учетом бокового обжатия.
23* 355
Примем часть функции напряжений Рдк 9) в виде F0K = R* [(2/? }f Qf (1) dQ* - R {J / (1) dQ* +
4- ^ qQ*) sin2 0 + cos2 0|J,2 (s/q2] . (20)
|
|
|
Фиг. 10. Эпюры напряжений в полукруглом диске в полярных координатах от равномерно распределенной нагрузки по криволинейному контуру и нагрузки, распределенной по прямолинейному контуру по закону Јq3/2 (теоретически). |
Тогда напряжения акг, ае, выразятся формулами:
DF0K, d*F0K
R ~ r2q ' bq 1 яу' да —
= (Rgf (1) - Rf (1) + q)sin2 Є + cos2 9 - L j q2 <Q}dQ +
F 2 cos 29 (4- RQf (1)----- i - Rf (1) 4" 4- j f Q2 MdQ2) (21)
Ae = -^r • ^ = №/ (0 - Rf (0 + <?)sin2 0 + cos29^2 (0); (22)
----- Vе! + J<72(0)rfe) sin 29; (23)
F^ = - rU!4dQi-l\q2lQ)dQ']; (24)
О 0
Где q — равномерная нагрузка на криволинейном участке контура диска;
02(о) — нагрузка на прямолинейном участке контура диска.
Функция (20) удовлетворяет полностью всем граничным условиям и уравнениям равновесия. Функцию, дающую нулевые значения на контуре Foi(Q> в), примем в прежнем виде [уравнение (13)]. Тогда напряженное состояние полудиска выразится по формулам (7)—(9) или (14)—(16), где а*, о* и т*9 принимаются по формулам (20)—(23).
Если н&грузка по прямолинейному контуру распределена по закону <72(q) = —то при одном нулевом члене мы получим элементарное решение для простой балки по формуле Навье с учетом бокового обжатия на фиг. 11, позиция 0.
При нулевом и одном первом члене ряда мы получим эпюру а9 (фиг. 11, кривая /).
Кривая III получена при одном первом члене ряда с функцией (12) при t, m,l = 1, п = 100.
Для сравнения приведена экспериментальная кривая IV, полученная при загружении диска равномерно распределенной нагрузкой по криволинейному контуру от оплетки при намотке на поворотном столе ДН-5.
Как видно из фиг. 11, растягивающие напряжения а0 более чем в 2,5 раза превышают значения, полученные из элементарного решения по формуле Навье (позиция 0). Наиболее близки к экспериментальной кривые I и II,
Первая получена при использовании элементарного решения в качестве первого приближения, вторая — при использовании в первом приближении одного первого члена аппроксимирующей функции (13).
Аналогичные результаты можно получить и для нагрузки, соответствующей второму виду загружения.
|
/.77 р9 2г?8 3,22j; |
|
Напряжений о0 в сечении диска я -к - от равномерно распределенной |
|
V4 |
|
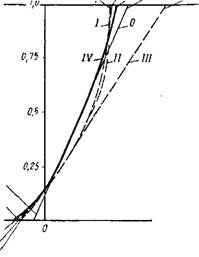
0 0,2856. IVOWiq, 1 0,7937- 110,7575 то,7 2 Фиг. П. При 0 = |
|
Нагрузки по криволинеиному контуру диска и нагрузки, распределенной по прямолинейному контуру по закону (q> == —2,5?q3/2: О — при одном нулевом члене ряда по формуле Навье; I — при нулевом и одном первом члене ряда; II — при одном первом члене ряда; III — прн одном первом члене ряда (другой вид аппроксимирующей функции); IV — кривая, полученная из эксперимента. |
Сравнение экспериментальной эпюры на фиг. 6, а и 11 (кривая IV) с теоретической на фиг. 10 и 11 (кривые I и II) показывает,
Что при первом виде загружения довольно близкое совпадение можно получить уже при одном первом члене аппроксимирующего ряда. Некоторое несовпадение можно объяснить тем, что был принят несколько иной посравнению с экспериментальным закон распределения давления под опорами и при вычислении экспериментальных напряжений использовался постоянный модуль упругости при сжатии.
Таким образом, в заключение можно сказать, что полукруглая форма проста в изготовлении. Она также позволяет равномерно и плавно распределить по всей криволинейной поверхности диска давление от оплетки. Этим создаются более благоприятные условия для работы арматуры и бетона при многократных нагрузках. От равномерно распределенной нагрузки в диске создается равномерное дополнительное обжатие, уменьшающее растягивающие напряжения, одинаково действующие при обоих видах загружения. Если по криволинейному контуру действует еще и трение, то нагрузка от оплетки уже не будет равномерно распределенной, и работа диска в одном случае может улучшаться, в другом ухудшаться. Причем степень улучшения или ухудшения работы ригеля зависит от величины трения.
Вообще трение неблагоприятно действует и на работу арматуры и бетона.