ПРИМЕНЕНИЕ ЖЕЛЕЗОБЕТОНА МАШИНОСТРОЕНИИ
Расчет осесимметрично загруженного сплошного цилиндра конечной длины
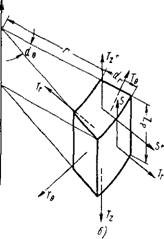
Уравнения равновесия. Рассмотрим тело вращения — круговой сплошной цилиндр, на который воздействует осесимметричная нагрузка. Будем пользоваться цилиндрической системой координат г, 0, г (фиг. 4, а), причем за ось вращения примем ось 2.
Вследствие симметрии тела и действующей на него нагрузки, напряженное состояние в произвольной точке цилиндра не зависит от координаты 8 и будет определяться четырьмя компонентами: Т„ Т„ Тг и S (фиг. 4, б).
|
=0; (65) 0. (66) |
Уравнения равновесия представляются в такой же форме, как и в случае плоской задачи:
ДЛ _L 4- TR~TI Дг ' дг ' г
DS, dTz S _
Дг ' г
Дг
Фиг. 4. К выводу уравнения равновесия в цилиндрических координатах.
Уравнения (65) и (66) удовлетворяются тождественно, если неизвестные усилия выразить через функцию F (г, z) по следующим формулам:
|
T, |
|
+ |
|
Дг2 |
|
Дг |
|
(67) |
D2F, J dF _ m 1 d2F 1 d/7
Т - 1
0 Л дг2
|
R _ 1 d2/7 . <j і у ------- ■ , ^ 2 Л о/2 |
|
(68) |
D2F
Дгдг
Будем искать решение системы уравнений (65) и (66) в форме
Тг - Т<0) -Ь ТГ;
Т тчо) , гр(к). J в = 1 8 ТМ і
|
(к) |
Тг = Т<0) + т<х);
(К).
S(0) + S
|
Т<°>. ..,, s |
|
(0) |
|
Где |
|
7f>.............. 5 |
|
(к) |
Решения, дающие нулевые значения усилий на поверхности тела и удовлетворяющие условиям равновесия; - решения, удовлетворяющие граничным условиям и условиям равновесия.
Введем безразмерные координаты
(-1<Б<1); 9 = ^. (О < 9 < 1), (69)
Где h — половина высоты цилиндра;
Г0 — радиус цилиндра. Перепишем формулы (67) в новых переменных:
_ _1________ 1_ J_____ 1 dF
R - ' q ' зі* т" гз • Q2 • dQ;
T ___WJ_ <PF___________ 1_ dF_
4 \ Q ' e2 ' dQ
* rl ' Є ' 5 — __ 1 1 d*F
Hrl Є '
По аналогии с уравнениями (68) представим функцию F (9, 5) в виде двух слагаемых
F(9, Е) = Fm (9, E) + F(K)(Q, Е), (71)
Каждое из которых будем рассматривать как
Fm(9, l) = ^amnR0n(q)Z0l}ay,
FM(9, =
Где m = 1, 2, 3, . . .; п = 1, 2, 3...................................
Подставим F(0) из формулы (72) в формулы (70) и потребуем выполнения нулевых значений соответствующих усилий на поверхности; при этом положим m = п = т. Это сделает задачу менее громоздкой, но для достижения определенной точности количество слагаемых в суммах должно быть увеличено.
|
S ■0)~ J lR |
|
Om .3 ^ - і |
7F > (9 = 1) = V а» '~ 2'оп, + 4 • Zom) '=== 0;
R0 h* Q 1 ,3
(73)
7f >(і = ± l) = "IT Zom = 0;
40) і Q = M V^
|
Zom — 0. |
" = ±1)
Из уравнения (73) легко находим, что
Zom (I = ± 1) = Z'om (а = ± 1) -= 0. ( )
Выбор функций RomiQ) И Zomd)- Любая ПОЛНЭЯ СИСТеМЭ замкнутых на соответствующих интервалах функций, удовлетворяющая условиям (74), может быть использована для решения задачи. В работах [7] и [8] при расчете пластинок, балок стенок и т. п. широко используются степенные функции. Для рассматриваемой задачи последние могут быть представлены в виде
Rom = (е — i)2em+2;
Zom = (f~ l)m+1, пг=\, 2, 3, ... (5)
Филоненко-Бородичом М. М. [2] введены функции, названные им косинус-биномами, которые для задачи о расчете сплошного цилиндра записываются так:
Rom = cos тщ — cos (т + 2) jtq;
Zom — cos тлі — c°s (tn + 2) я£.
Выбор той или иной системы функции Rom, Zom следует увязывать соответственно с функциями RK и ZK определяемым видом поверхностной нагрузки. Очевидно, предпочтения будет заслуживать та система функций Rom, Zom, которая в комбинациях с функциями R^ и ZK будет образовывать наиболее легко интегрируемые выражения.
Определение функций RK и ZK. Функции RK и ZK должны удовлетворять условиям равновесия и условиям на поверхности тела. Их можно получить как частный интеграл системы уравнений (65)—(66) при каких-либо упрощающих решение предположениях. Эти предположения следует основывать, исходя из вида загружения.
1. Цилиндр загружен произвольной нагрузкой, распределенной по боковой поверхности, а торцы его от нагрузки свободны, т. е.
Т2(£=±1)=0; (77)
5(е= 1, 1 = ± 1) =0,
То, положив в уравнениях (65)—(66) 5 = 0, тем самым перейдем к рассмотрению напряженного состояния диска единичной толщины, загруженного по краю полярно симметричной нагрузкой—Р. Как известно, при таком нагружении в диске будет
Отсюда при указанном нагружении, в качестве частных интегралов (65)—(66), можно принять
Т<к> = Т[к) = — р (£); 5(к) = 0, (78)
А из уравнения (66) получить, что
T[K) = RK(Q). (79)
Если имеется возможность (исходя из вида нагрузки или по экспериментальным данным) предположить закон распределения ТІК) — RK (q), то этим следует воспользоваться. В крайнем случае можно положить Т[к) = 0, что приведет к тому, что в результатах решения для достижения необходимой точности придется учесть большее количество слагаемых в выражениях (68).
2. Боковая поверхность цилиндра свободна от нагрузки, а торцы его нагружены произвольной нормальной нагрузкой.
Подставив в формулы (70) функцию F(,c) (q, £) из формул (72), получим
Т(к> — 1 Rk 7" , 1 Як 7 . ' - г0Л» ' q + г3 • e«
-(К) _ 1 ( Як Як
' I
|
Гр\_к) _ і - ч к 7 . 1 0 '— "------------------- I Г0 Т(к) 1 Як 7 1 г — ~з — к, г0 в О(К) _ 1 Як 8 Положим, в формуле (80) ZK = const = 1; запишем условия задачи: Пк) (8 = 1) (81) Го у Пк)(£ = ± 1)=4-4" = -^(е); (83) Го у Очевидно, /?к легко определить из выражения (83), причем для удовлетворения условия (81) должно быть R'K (е = 1)=0. |
Поскольку RK будет содержать произвольные постоянные интегрирования, то это условие легко удовлетворяется. Нетрудно также убедиться, что выражения (81)—(84) удовлетворяют уравнениям равновесия (65)—(66).
3. Произвольной нормальной самоуравновешенной нагрузкой нагружен только один торец цилиндра, например, определяемый координатой ^ = 1, т. е.
> (Q = 1) = ■^ Z'K + 4 ,2К = 0; (85)
К у I — ?(е) при I = + 1,
* " ^ в *"■( 0 при Б------------------------- 1; ( )
S(K)(Q= 1, 1 = ± 1) =--- = 0. (88)
RQh Є
Очевидно, что в этом случае RK и ZK следует подобрать такими, чтобы выполнялись условия
Ze(E = l) = l; ZK(l = - 1) = 0; Z'K(Ј=± 1)=0; /?к (Q = 1) = 0; R'K (Q = 1) = о. В качестве функции ZK можно принять, например,
А функцию RK определить двукратным интегрированием из выражения (87). Полученные при этом две постоянные интегрирования позволят удовлетворить требуемым условиям.
Второй вариант решения задачи. Нетрудно убедиться, что уравнения (65)—(66) удовлетворяются тождественно, если принять следующие решения [3]:
Т - — ^L - Т ^ ■
Г=~ г ' дг2 ' 0 дг2 ' 1 ( (PF dF \
П^^(-^-^г); (89)
S ■ - J_ (М- _
Г \ дг дг дг
Где F — функция напряжений, которую как и в вышеизложенном варианте (переходя к Переменным q, £) представим в виде
F = F0(Q> L).+ FK(q, Б), (90)
Причем
Me. s) = 2 апЯот (q) zom (£);
_ _ (У1) FAQ, =
Решение (89) также представим в виде двух слагаемых по формулам (68).
Подставим F„ (q, Б) из формулы (91) в формулы (89) и потребуем выполнения нулевых условий на поверхности
TOC \o "1-3" \h \z 7f > (Q = 1) = т^г 2 ат^отХ>т - 0; (92)
7f > а = ± О - У ат {\Жот - = 0; (93)
6Л0 \ г0
Те' — ~^^CLmR0mZ0m\ (94)
S<0)(! = Г')=о. об)
Очевидно, для выполнения условий (79) функции R0nt, Zom должны удовлетворять условиям
- 1) = i?;m(Q - 1) - 0; _
Zem(6=±l) = Z^1(6 = ±l) = 0. ( ]
Условия (96) полностью совпадают с условиями (74) первого варианта решения. Отсюда функции Rom и Zom могут быть приняты по формуле (75) или (76). ___
Подставим в формулы (81)—(84) функцию FK (q, g) из формулы (91), получим
ТГ (q = I) ^ ~ RKZK-, (97)
T\k)=±-RX - (98)
7f > - — RK - — RK \ ZK; (99)
'oQ I ro ro
Рассмотрим те же случаи нагружения цилиндра, что и в первом варианте решения.
1. Боковая поверхность нагружена произвольной нагрузкой. Торцы свободны. Положим, что в формулах (97)—(100)
RK = const =1 (101)
И, записав условия задачи, получим
TiK)(Q^\) = 7^-Z"K = - p(l), (102)
S(K)(e = l, l = ± l)=-±^Z'K = 0- . (104)
Т(к> — 1 О 7" 1 0 — Кк^к -
Эти условия легко выполняются только для случая постоянной нагрузки по боковой поверхности цилиндра Р (£) = const. В общем случае, Р = Р (£), боковая поверхность оказывается нагруженной также сдвигающими усилиями. Очевидно, проще частное решение подбирать так же, как и в первом варианте решения.
2. Боковая поверхность цилиндра свободна от нагрузки, а его торцы нагружены произвольной нагрузкой q (q).
Положив в выражениях (97)—(100) Z = const = 1, получим, что условия
7f> (е = 1) = 0, 5(К)(Є= 1, Б = ±1) = 0
Выполняются автоматически. Функция RK определится из уравнения (98): « *
* ' RK~roRK = — rlq(Q)Q. (105)
Сравнивая первый и второй варианты решений, заметим, что второй по сравнению с первым особых преимуществ не имеет.
Уравнение Кастильяно. Приведенные выше решения удовлетворяют уравнениям равновесия. Для того чтобы они удовлетворяли также и уравнениям совместности, потенциальная энергия деформаций, выраженная через напряжения, должна принимать минимальное значение, т. е.
6V = 0, (106)
Где 6 — символ вариации;
V — потенциальная энергия деформации, которая в случае осесимметричной задачи цилиндра (при принятых выше относительных координатах q, £) записывается так: її
К = - ПГ \[т2г+т\+ т\- 2р (туг9 + T, TZ + TrTz) +
-io +2(1 — |i)S2]Qdedg; (107)
Здесь p — коэффициент Пуассона. 332
Вариационное уравнение (106) равносильно системе уравнений ^-=0 (n= 1, 2, 3, ..., п). (108)
Подставив в формулу (108) уравнение (107), учтя при этом формулы (68), получим систему п уравнений типа
I 1 {(ГЖ + 7F >) ТІЇ + (TZ + ГІ->) ТІЇ + (П°> + 7F >) ПІ -
-і о
— Н [(т% + г<к)) {тії + тії) + (Тй + 7f >) [тії + тії) +
+ ( TZ + 7f >) (ТІЇ + тЯ>)] + 2 (1 + rt x
X(S^ + Sw)S^}QdQdl = 0. (109)
Исследуемая область односвязана, поэтому, согласно теореме Мориса Леви, V не должно зависеть от ц.. Не нарушая общности решения, положим поэтому ц. = 0, что значительно упростит задачу. В формуле (109) принято
^
Перенесем в уравнении (109) члены, зависящие от нагрузки, вправо, получим [вместо уравнения (109) ]
J J(7-M + ГМ + Т&Т% + 2s№)QdQdl =
— і о
= - j' f (Пк)ТІЇ + 7f >ТІЇ н - тік)Тії + 2SKST) QdQdl. (Ill)
—і о
Параметры am, подлежащие определению, содержатся в левой части формулы (111). Система уравнений для их определения получается по следующей схеме [7]: при п = 1 индексу m последовательно даются значения 1, 2, 3, . . . — получаем первое уравнение системы; затем при п = 2 m даются значения 1, 2, 3, . . . — получим второе уравнение и т. д. Например, для решения задачи с точностью до двух параметров элементы системы уравнений с двумя неизвестными ах и а2 определятся по формулам:
Б1Л= J I ТІЇ T? U ТІЇ Tfn ТІЇ ТІЇ+ 2SZSZ) QdQdl,
— і о
П = 1, m - - 1;
= І І (ТІЇ Тії + Тії Тії + ТІЇТІЇ + 2SpS\0)) е dQ dl,
— і о
П — 1, m = 2;
І \(тіїтії + ТІЇТІЇ + ТІЇТІЇ + 2^№)Qd<>dl,
— і о
П = 2, m = 1;
Ms -- І / (Тй> rg> + Tg? + П°2> 7-® f 2SW) Q dQ
— і о
N = 2, m = 2; (112)
Alp = — j J (7f > Tfi TP f J? + 7f > + 2S(K)Sl0)) q dQ - і о
N = l; (113)
^ = - Я (7f > - ь г<к> + Пк) ffJ 2S(K)Sf)Q dQ dl,
N = 2.
Нетрудно убедиться, что система уравнений для определения параметров будет симметричной относительно главной диагонали.
Примеры. Изложение примеров расчета мы построим следующим образом. Поскольку выражения (112) от нагрузки не зависят, т. е. являются неизменной частью системы уравнений, мы их вычислим в первую очередь. Затем в каждом частном случае загружения будем вычислять только грузовые члены формулы (113).
Ставя своей целью проиллюстрировать метод, мы не будем также стремиться к большой точности и ограничимся только первым приближением.
Вычисление бп. Принимаем т = 1. Тогда из выражения (75) получим
Яоі = (е - і)2 е3; 201 = (і2 - і)2 Iа.
Из формулы (112) имеем
1 1 . - , ,2 ' v
„ __ „ , , _________ - У, 2 I *01*0. 7" 7 , #01 7'2\j_
Jna, - а, | | —------- Z01Z01 - р j
■ 1 о
„2
DQ dl
Произведя необходимые вычисления, получим
|
6 • |
1 0,0042 —i-5- - f 0,0227
R$h* ' ' r*h2 rQ
Приняв h -- r0, получим
6, t - 0,0356 .
'o
Рассмотрим теперь некоторые простейшие случаи нагружения. 1. Боковая поверхность цилиндра нагружена постоянной нагрузкой - Р = const (положим также, что h = г0).
Из формулы (78) имеем, что для этого случая можно принять pW _ - рік) __ р
Из формулы (113) имеем
І 1
Аір= ■
— і о і і
Rgi „ Rgi. — Z01 + - г - Z01 I QdQdl.
- 1 о
Подставив сюда значения р01, Р01, ZQ1, Z01 и выполнив необходимые операции, найдем, что А1р = 0.
Следовательно, при рассматриваемом случае нагружения будем иметь [как это следует из уравнения (68) ]
Т = ^С) = ____ Р;
Г, = Г<к> = - Р; Г2 = S = 0.
2. Боковая поверхность цилиндра нагружена нагрузкой, распределенной по закону
/ 1 _ £3\ 4 р
РШ = Ро(—2"1) =^(1-^.
Как и ранее, примем, что
= = — />(£) = —^-(1 — pW _ = о. Вычислим А, р. Из формулы (113) имеем і 1
|
1 'о |
|
Чи |
^01 + '
-і о
Подставляя в последнее выражение значения р01, Zqj, Z01 и Р (£) и произведя необходимые вычисления, получим
А, р 0,00277-^f,
Отсюда
_ _ 0.С0277 з _ з
1 ~ б„ ~ 0,0356 - 0-°'7WVo.
Следовательно, для рассматриваемого случая нагружения цилиндра будем иметь
Tr = Ро j^i [Є2 (Є2 - I)2 -2 (15£* — 12|2 + 1) + (Q — 1) (5Є - 3) (£2 - І)212] -
-^(i-iv};
|
|
|
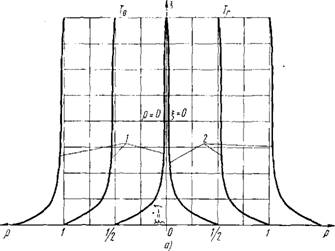
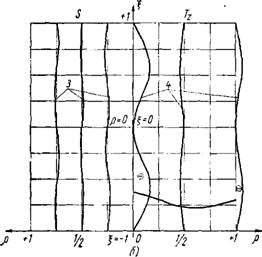
Фиг. 5. Эпюры усилий Tr, S, Tz: |
Tt = P0 {«1 [2 (10Є[9] - 12q + 3) - (e - 1) (5Q - 3)] (I2 - l)2 l* - 1(1 - £3)4 J ;
Tz = P0 {ai [2 (10Є2 - 12Q + 3)J (Ј2 - l)2 I2};
S = P0 Ke (e— 1)(5q — 3) 21 (31 - 4|2 + 1)}.
Вычисленные по этим формулам значения соответствующих величин сделаны в табл. 1—4, а также показаны графически на фиг. 5, а и б.
Нетрудно заметить, что первое приближение для Тг и Тр очевидно, вполне достаточно.
|
Значения величин Тг : Р0 |
|
Значения величин : Р0 |
|
337 |
Величины Тг и 5 требуют дальнейших уточнений. Этого и следовало ожидать, поскольку частные решения и 5(,с)были приняты равными нулю.
|
Таблица 1
|
|
Таблица 2
|
|
22 Сборник 1835 |
|
Значения величии Тг : Р0
|
|
Значения величин S : Рп |
|
Таблица 4
|