ПРИМЕНЕНИЕ ЖЕЛЕЗОБЕТОНА МАШИНОСТРОЕНИИ
Воздействие многократно повторной нагрузки на железобетонные конструкции
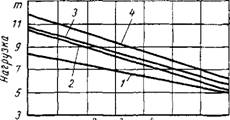
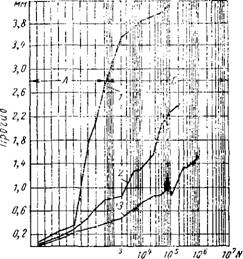
Обычные железобетонные конструкции. Влияние многократно повторной нагрузки на работу железобетонных конструкций изучалось в основном на балках. В многочисленных работах, было установлено, что прочность железобетонных балок снижается при воздействии повторной нагрузки, причем снижение прочности происходит тем в большей степени, чем меньше характеристика цикла q и больше число повторений нагрузки N (фиг. 15). По-
Прежнему N и q остаются важнейшими факторами при прочих равных условиях.
После воздействия повторной нагрузки на изгибаемые элементы в арматуре растянутой зоны возникают остаточные растя - 6 i07N гивающие напряжения, что, в свою очередь, вызывает деформации упругого сжатия на участке около нейтральной оси и деформации упругого растяжения в верхних волокнах балки [18]. Причем растягивающие напряжения при определенных условиях могут превышать предел выносливости бетона на растяжение и вызывать образование трещин.
Разрушение балок при воздействии повторной нагрузки может происходить по одной из перечисленных ниже схем: разрушение сжатой зоны бетона, разрушение от главных растягивающих напряжений, разрушение вследствие нарушения сцепления между бетоном и арматурой, разрыв арматуры в зоне чистого изгиба.
На характер разрушения балки с арматурой только в растянутой зоне, как было установлено Кеслером и Чангом [28], может влиять при прочих равных условиях только величина повторной нагрузки (при q = const).
|
10 10' 10' 10ч 10' КоличестЬо циклоб |
|
Фиг. 15. Влияние числа нагружений и харак теристики цикла на выносливость железобе тонных балок: |
|
Q = 0,15; |
|
2 — q — 0,33; 4 — Q = 0,70. |
|
3 — Q = 0,50; |
При приложении достаточно высокой повторной нагрузки (0,8Рразр) разрушение происходит от главных растягивающих напряжений при небольшом числе циклов; при приложении меньшей нагрузки (примерно 0,6Рразр) разрушение балки происходит вследствие усталостного разрыва арматуры при большем числе циклов. В общем случае наиболее часто встречающийся характер разрушения — это усталостный разрыв арматуры, причем обрыв стержней носит хрупкий характер, без образования шейки. 64
Слабое развитие остаточных деформаций в арматуре приводит к недоиспользованию несущей способности сжатой зоны бетона, что и предопределяет этот вид разрушения.
Как указывается в работе [15], величина разрушающей нагрузки зависит от частоты приложения этой нагрузки, характеристики цикла q, прочностных и деформативных свойств стали и бетона.
В зависимости от преобладания тех или иных факторов величина разрушающей многократно повторной нагрузки может колебаться от 0,5 до 1,0 величины разрушающей статической нагрузки.
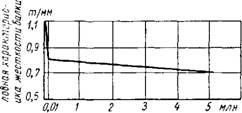
С ростом числа приложений нагрузки (вызывающей напряжения ниже предела выносливости) происходитснижение жесткости изгибаемых элементов [15] и [22], причем это снижение наиболее ^ [5]Ощутимо при первых циклах нагрузки и имеет тенденцию к стабилизации при дальнейшем повторении нагрузки (фиг. 16). Величины остаточных прогибов по отношению к упругим в опытах составляли для некоторых балок 100—120% [15].
Ниже приводятся соображения по расчету обычных железобетонных конструкций с учетом специфики их работы в машиностроении.
Расчет на выносливость в действующих нормах ведется по упругой стадии с использованием треугольной эпюры напряжений в сжатой зоне и без учета работы растянутой зоны.
Как уже указывалось, расчетные характеристики материалов в нормах приняты, будучи определенными на базе 2-Ю6 циклов.
Значительное развитие остаточных деформаций во время воздействия повторной нагрузки учитывается введением в расчет повышенных соотношений модулей упругости арматуры и модулей деформации бетона »'. Значения п' в нормах вычислены
£
Делением коэффициента приведения п = на отношение мо-
|
Количеств циклоі |
|
.Фиг. 16. Влияние числа циклов на развитие остаточных прогибов в железобетонных балках при е = 0,23 и К = 0,52. |
Дуля деформации бетона после воздействия повторной нагрузки к модулю упругости при однократном загружении, причем это отношение принято дифференцированным в зависимости от марки бетона.
|
65 |
Для бетонов марки «500» и выше коэффициенты приведения следует принимать с учетом числа циклов выше 2-Ю6 по данным табл. 3.
Для марки ниже «500» до получения достоверных экспериментальных данных значения п' можно вычислять после определения величин предельных деформаций ползучести [23].
Как уже упоминалось выше, в настоящее время возможен подход [13] к оценке предельной величины остаточной деформации при повторной нагрузке путем вычисления предельной вели-, чины этой деформации при действии условной длительной нагрузки с напряжением, равным стах (см. фиг. 10).
Следовательно, для предельных значений деформаций (для числа циклов, значительно больше 2 • 106) это отношение удобно' вычислять в каждом конкретном случае после определения ф(=00. Численное значение отношения полной деформации к первоначальной, Т. е. <Рг=оо + 1, и будет тем множителем, который надо ввести к п для получения значения «'; тогда
П'=п(<р,=„ + 0- (14)
Подставляя значение п' в расчетные уравнения, вычисляют действующие напряжения, которые затем сравниваются с расчетными сопротивлениями бетона и арматуры на выносливость; при этом расчетные сопротивления бетона вычисляются с учетом предполагаемого числа циклов нагрузки.
Предварительно напряженные железобетонные конструкции. Создание предварительного напряжения резко повышает выносливость и жесткость конструкций при воздействии повторной нагрузки. В результате предварительного напряжения снижается перепад напряжений в арматуре (т. е. она работает при значительно более высоком q) и практически исключается появление растягивающих напряжений в бетоне растянутой зоны при эксплуатационных нагрузках.
По данным Троицкого Е. А. [24], при равных нагрузках амплитуда деформаций бетона в сжатой зоне обычных ненапряженных балок была больше, чем в предварительно напряженных балках, примерно на 20%, а в растянутой зоне соответственно на 60%; амплитуда прогибов железобетонных балок в среднем была в 1,5 раза больше амплитуды прогибов предварительно напряженных балок. Кроме того, остаточные прогибы обычных железобетонных балок нарастали на всем периоде действия повторной нагрузки, в то время как для предварительно напряженных балок они быстро стабилизировались и составляли незначительную долю от упругого прогиба.
Характер разрушения предварительно напряженных конструкций при воздействии повторной нагрузки, как показывают многочисленные исследования, остается по существу таким же, как и для обычной железобетонной балки, т. е. балка может разрушаться вследствие: разрушения бетона в сжатой зоне или в зоне действия главных растягивающих напряжений; разрушения пред - 66 варительно напряженной арматуры; потери сцепления арматуры с бетоном.
Величина разрушающей нагрузки зависит от многих факторов, это, в первую очередь, степень предварительного напряжения, процент армирования, вид арматуры (гладкая или периодического профиля) и т. д.
Для иллюстрации работы предварительно напряженной конструкции на многократно повторную нагрузку может быть ис
|
Пользована диаграмма,
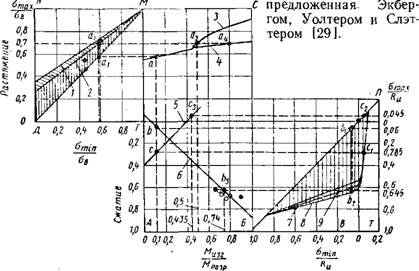
Фиг. 17. Условная диаграмма работы предварительно напряженной конструкции на многократно повторную нагрузку: |
1 — стержневая арматура; 2 — высокопрочная проволока; 3— оптимальное армирование; 4 — излишняя арматура; 5 — бетон в растянутой зоне; 6 — бетон в сжатлй зэне; 7 — N = 2. 10'; 8 — N = 10'; 9 — N = Ю«.
На фиг. 17 показаны хорошо известные диаграммы Гудмана- Джонсона для арматурной стали (в левом верхнем углу) и для бетона (в правом нижнем углу; для бетона она перевернута). Для бетона построены три кривые — экспериментальные для числа циклов 2 и 10 млн. и экстраполированная для 100 млн. циклов. Средняя часть рисунка занята условной диаграммой изменения напряжений в изгибаемом элементе арматуры и в крайних волокнах сжатого и растянутого бетона с ростом однократно прикладываемой внешней нагрузки. Величина нагрузки, отложенная
По оси АБ, выражена в относительных единицах и равна ^!изг ;
Мразр
Ліизг — действующий изгибающий момент; Мразр — разрушающий изгибающий момент при однократном нагружении.
5* 67
Напряжения в бетоне и арматуре также отнесены к прочности бетона и арматуры. Помня об этом, ниже, объясняя эту диаграмму, мы позволим себе слово «относительный» применительно к нагрузкам и напряжениям в отдельных случаях опускать.
С ростом нагрузки происходит увеличение напряжений в арматуре; в бетоне происходит снижение сжимающих и появление растягивающих напряжений в крайних волокнах растянутой зоны, и увеличение сжимающих напряжений в крайних волокнах сжатой зоны. Когда напряжение превзойдет прочность бетона на растяжение, в растянутой зоне образуется трещина. В момент образования трещины происходит прирост напряжений в арматуре, после чего она некоторое время продолжает работать упруго, но при дальнейшем увеличении нагрузки до разрушающей напряжения в арматуре достигают предела текучести.
Такая картина изменения напряжений наблюдается при достаточно слабом, или, «оптимальном» армировании, когда несущая способность арматуры используется полностью.
При сильном насыщении элемента арматурой она работает упруго фактически до момента разрушения по сжатому бетону, и ее несущая способность остается значительно недоиспользованной.
Посмотрим, как будут изменяться напряжения в арматуре и в крайних волокнах бетона, если на этот элемент начнет многократно действовать изгибающий момент (Мизг), меняющий периодически свое значение от М'т\п до М'тах (М'т-т и Mmax — минимальный и максимальный изгибающие моменты в цикле). При рассмотрении работы конструкции на повторную нагрузку в стадии разрушения момент Мтах является также и разрушающим моментом.
Откладываем относительную величину максимального изгибающего момента по оси нагрузок, т. е. по оси А Б (зададимся, к примеру, величиной Mmin = О. Шразр). Проводим вертикальную прямую до пересечения в точке а с линией, выражающей изменение напряжений в арматуре в верхнем среднем квадрате, ііереносим величину этого напряжения на диаграмму выносливости арматуры, для чего из точки а проводим горизонтальную линию до пересечения с диагональю ДМ, которая представляет собой ни что иное, как линию постоянной минимальной нагрузки. На пересечении получаем точку а1. Опуская из точки ах перпендикуляр на ДГ, найдем величину минимального напряжения аат\п = 0,58 ав, действующего в арматуре при приложении Mmin = 0,1 мразр.
Когда несущая способность арматуры используется полностью при воздействии многократно повторной нагрузки, напряжение в ней <татах равно пределу выносливости. 68
При найденной величине минимального напряжения оа min = = 0,58 ав значение оа отах легко будет найдено, если из точки а2 опустим перпендикуляр на ось ДН\ при этом найдем oamay[ = 0,7ав. Точка а2 получена в предположении, что конструкция армирована высокопрочной проволокой. При применении стержневой арматуры точка а2 будет лежать соответственно на линии 1 — «стержневая арматура».
Посмотрим, какова будет величина изгибающего момента, когда максимальное напряжение в арматуре равно пределу выносливости. Для этрго из точки а2 проведем направо горизонтальную прямую до пересечения с линией арматуры и получим точку а3. Опуская из точки а3 перпендикуляр на ось АБ, находим величину разрушающего изгибающего момента Мрая а при воздействии повторной нагрузки; его величина будет Мраз, а = 0,5Мраз.
Для переармированного сечения точка пересечения с линией , арматуры попадет в а4, и разрушающий момент по арматуре значительно увеличится. В результате этого можно сделать вывод, что введение дополнительного количества арматуры будет улучшать работу предварительно-напряженной железобетонной конструкции на выносливость.
Посмотрим теперь, какой будет разрушающий момент по сжатому бетону при действии многократно повторной нагрузки.
Находим точку b пересечения вертикальной прямой, отстоящей от оси АГМ на расстоянии М mln =0,1, с линией, показы-
Мраэ
Вающей изменение напряжений в бетоне сжатой зоны. Из точки b проводим направо горизонтальную прямую до пересечения в точке Ь1 с диагональю БП. Диагональ БП также является линией постоянных, т. е. минимальных напряжений.
Опуская из точки Ьг перпендикуляр на ось 777, найдем величину напряжения в сжатой зоне бетона <тт1п = 0,06 Ru при приложении МОМеНТа Mmin = 0,1 Мраз.
При полном использовании несущей способности сжатой зоны бетона при воздействии многократно повторной нагрузки напряжения в крайних волокнах будут равны пределу выносливости бетона, величину которого при данном значении аб min найдем, опустив перпендикуляр из точки Ьг на ось 777; при этом получим ^ б max = 0.645Ru = Ry.
Найдем теперь величину изгибающего момента, вызывающего в бетоне напряжение, равное Ry. Для этого из точки й2 проводим налево горизонтальную прямую до пересечения с линией сжатого бетона в точке Ь3. Опуская из точки Ь3 перпендикуляр на ось АБ, найдем Мраз. б = 0,74Мраз. При армировании элемента применительно к работе на статическую нагрузку, т. е. при «Оптимальном армировании», величина Мраз. о оказывается существенно больше
69
Величины Мраз. а■ Это указывает на то, что «оптимальное армирование» оказывается далеко не оптимальным при работе этого элемента на многократно повторную нагрузку, так как несущая способность сжатой зоны значительно недоиспользуется.
Обратимся теперь к растянутой зоне бетона. Хотя полное использование несущей способности бетона в растянутой зоне нё* явится причиной быстрого разрушения элемента, тем не менее оно вызовет образование трещин, которые для большинства конструкций машин будут нежелательны. Таким образом, определим величину изгибающего момента трещинообразования при воздействии многократно повторной нагрузки.
Находим точку С пересечения вертикальной прямой линии
= 0,1 с линией, выражающей изменение напряжений в бе-
Раз
Тоне растянутой зоны с ростом нагрузки.
Поступая аналогично изложенному выше, находим точку сг, затем с2 и, наконец, с3. Опуская из точек сх и с2 перпендикуляры на ось ТП, найдем величины напряжений в бетоне растянутой зоны — растяжение <rmin = 0,045#а и сжатие атах = 0,285 Ra. Опуская перпендикуляр из точки с3 на ось АБ, найдем величину момента трещинообразования при действии повторной нагрузки — Мт = 0,435 Мразр. Естественно, что его величина оказалась меньше, чем разрушающие моменты по арматуре и бетону.
Анализируя описанную диаграмму, можно наметить мероприятия по повышению выносливости предварительно напряженных железобетонных конструкций. К ним относится, как уже указывалось, повышенное армирование растянутой зоны. Если мысленно перенесем линию работы арматуры выше, т. е. увеличим степень ее предварительного напряжения, то, очевидно, увеличится и разрушающий момент по арматуре при действии повторной нагрузки^ Если увеличим обжатие растянутой зоны, т. е. на диаграмме (фиг. 17) линию 5 «бетон в растянутой зоне» опустим параллельно самой себе вниз, то пропорционально увеличится и Мт.
Влияние упомянутых мероприятий на выносливость предварительно напряженных железобетонных конструкций подтверждается и экспериментально. На этой же диаграмме нанесены данные по испытаниям образцов с напряженной спиральной обоймой, проведенные Астровой Т. И. и Брайловским М. И. ( о — точки, полученные построением по диаграмме; • — экспериментальные точки). Образцы имели сильное насыщение арматурой и разрушились по бетону. На диаграмме не показаны линии работы арматуры и бетона. От диагонали ДМ отложена амплитуда напряжений в арматуре, которая была меньше допустимой. Образец разрушился по бетону, причем величина разрушающей повторной нагрузки составляла 0,8 от статической.
При отсутствии предварительного напряжения линия изменения напряжения в арматуре будет исходить из нуля (из точки Г),
В этом случае максимальный воспринимаемый момент при работе на повторную нагрузку оказывается существенно меньше.
|
(здесь Нагрузка). Повыше- |
|
0,53Р„ |
|
Раз. стат Статическая |
|
Стат |
|
0,1 0,3 0,5 0,7 0,9 10 |
|
КоличєсгпВо ци. плоб |
|
Фиг. 18. Влияние степени предварительного напряжения арматуры на развитие остаточных прогибов (/) железобетонных балок с ростом количества циклов (N) повторения нагрузки: |
|
= 0,35 ав; 2 — ст0 "" °'65 <V 3 ~~ °о А — статические загружения до Р |
|
І = 0,8 <т |
|
Шах' |
|
Б — пульсирующее действие нагрузки. |
В опытах Ксеркавена П. [11 ] при увеличении степени предварительного натяжения проволочной арматуры с 0,52сгв до 0,78сгв величина разрушающей повторной нагрузки при 106 циклах
До 0,8Рраз
Также увеличивалась с Рраз. стат ~ разрушающая ние выносливости предварительно напряженных железобетонных балок с увеличением степени предварительного напряжения арматуры подтверждается опытами Михайлова К. В. и Городницкого Ф. М. [17]. Авторы упомянутой работы рекомендуют поэтому для железобетонных конструкций, работающих на многократно повторную нагрузку, увеличивать степень натяжения арматуры до 0,75(Ту, вместо 0,65сгв, содержащейся в нормах. Эта рекомендация целиком и полностью может быть отнесена к предварительно напряженным железобетонным конструкциям машин.
 Увеличение степени предварительного напряжения повышает не только выносливость, но и жесткость, что является важным для конструкций машин. На фиг. 18 видно, что прогибы балок с сг0 = 0,86сгв после 105 циклов были в три с лишним раза меньше, чем у балок с сг0 = 0,65сгв.
Увеличение степени предварительного напряжения повышает не только выносливость, но и жесткость, что является важным для конструкций машин. На фиг. 18 видно, что прогибы балок с сг0 = 0,86сгв после 105 циклов были в три с лишним раза меньше, чем у балок с сг0 = 0,65сгв.
В качестве других мер, направленных на увеличение выносливости конструкций, является применение арматуры периодического профиля при натяжении ее в стадии изготовления на упоры. При натяжении арматуры на бетон, что имеет место при сооружении большинства железобетонных машин, рекомендуется применять все-таки гладкую проволоку, как обладающую лучщцми показателями по выносливости, чем проволока периодического профиля. Другой важной мерой для повышения выносливости
и жесткости конструкций является инъекция каналов, в которых расположена напрягаемая арматура при натяжении ее на бетон. При отсутствии инъекции рекомендуется принимать в расчетах пониженное на 15% значение модуля упругости бетона [24].
При расчете предварительно напряженных железобетонных конструкций машин с применением высокопрочного бетона значения п' следует принимать по данным табл. 3; для прочностей, меньших 500 кГ/см2, следует руководствоваться теми же соображениями, что и при вычислении п' для ненапряженных железобетонных конструкций, т. е. вычисляя предельную величину остаточной деформации ползучести по [23]. Очевидно, величина «', определенная таким путем, будет содержать в себе некоторый запас. Для проверки железобетонных конструкций на'выносливость авторы предлагают номограмму, которая позволяет для случая центрального сжатия и изгиба расчет на выносливость не производить, а ограничиваться расчетом только на прочность, на приведенные нагрузки.
Номограмма для проверки конструкций из обычного и предварительно напряженного железобетона на выносливость при изгибе и центральном сжатии. В действующих нормах [21] и [23] расчет на выносливость обычных железобетонных конструкций ведется по уравнениям сопротивления упругих материалов, т. е. принимается, что напряжения в сжатом бетоне и растянутой арматуре изменяются линейно при изменении нагрузки от Mmin до Afmax. Работа растянутого бетона при этом не учитывается. Расчет производится на нормативные нагрузки (с использованием в необходимых случаях коэффициента динамичности). Следовательно, по абсолютной величине максимальная повторная нагрузка не может превысить статическую расчетную нагрузку. Это положение также относится и к величинам напряжений, т. е. напряжение от максимальной повторной нагрузки не может превысить напряжение от расчетной статической нагрузки и не должно превышать расчетного сопротивления бетона. Но, так как расчет на повторную нагрузку выполняется с использованием треугольной эпюры распределения напряжения, а сами величины расчетных сопротивлений бетона и арматуры на выносливость меньше, чем при расчете на однократную нагрузку, то сечение, подобранное по расчетной статической нагрузке, может не удовлетворять требованиям по выносливости.
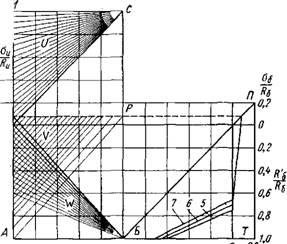
Все изложенные нормативные положения позволяют предложить номограмму для расчета на выносливость конструкций из обычного и предварительно напряженного железобетона (фиг. 19, а). Средняя часть номограммы представляет собой условные графики изменения напряжений в арматуре (£/) и бетоне (V и W). Увеличение напряжений с ростом нагрузки принято по прямым, согласно изложенному выше. Когда нагрузка равна нулю, напряжения для предварительно напряженных конструкций в арматуре
&
Ra 0,8
OA
|
И |
|
У З* І/ |
|
ОД 0,2 Ofi 0,6 ■ 0,8 Г Од min |
0,2 OA 0,6 0,8 1,0 0,8 0,6 OA 0,2
|
Фиг. 19. Номограмма для расчета предварительно напряженных и обычных железобетонных конструкций на выносливость: |
Mnotm min
|
Mt |
|
Hg |
A)
'расч
|
|
A—номограмма; б—пример расчета; 1 — стержневая арматура класса А-ІІ; 2—стержневая арматура класса А-ІІІ;3 — проволока периодического профиля; 4 —гладкая проволока; 5— =2-Ю«; 5—^=10'; 7—N=10»; U—установившееся напряжение растяжения; V — бетон в растянутой зоне; W — бетон в сжатой зоне; М — расчетный
Момент внутренних сил; Мподт—минимальный или максимальнный момент прн расчете конструкций на выносливость; Ra — расчетное сопротивление арматуры при
Расчете на прочность; Ra— то же, при расчете на выносливость; "ат;П' dg mjn — минимальные напряжения в арматуре и бетоне от повторной нагрузки; Rg — расчетное сопро-, тивление бетона при расчете конструкций на прочность (в зависимости от вида напряженного состояния Rnp илн Ruy, Rg— то же, при расчете конструкций на выносливость
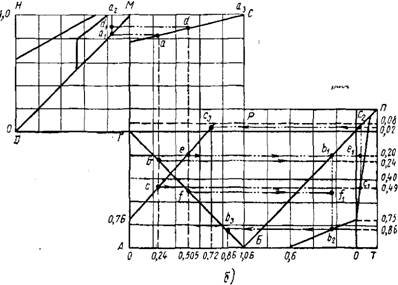
(Rnp - *„)•
И бетоне равны установившемуся напряжению. Для ненапряженных железобетонных конструкций это будут нули или напряжения от собственного веса. По оси АБ отложено отношение величины повторного момента к расчетному моменту внутренних сил (правая часть любой формулы расчета на прочность).
При построении номограммы принимается, что момент внешних сил при расчете на прочность равен моменту внутренних сил. Превышение второго над первым, естественно, идет в запас прочности. От нуля по оси АГМ отложены относительные единицы напряжений, равные отношению действующего напряжения в арматуре и бетоне к расчетному сопротивлению арматуры и бетона.
Данцая номограмма построена по тому же принципу, что и диаграмма на фиг. 17, с той лишь разницей, что по осям 'отложены расчетные относительные напряжения и нагрузки. Кроме того, поскольку трещины в предварительно напряженных конструкциях, работающих на повторную нагрузку, недопустимы, линии работы арматуры даны без всяких переломов.
Зная минимальную нагрузку, откладываем ее относительное значение по оси нагрузок АБ и находим линии изменения напряжений в арматуре и бетоне, соответствующие нашему случаю.
Для ненапряженного железобетона работе арматуры соответствует на диаграмме линия ГС, а для сжатого бетона—ГБ\ растянутый бетон не учитывается. Заметим, что расчет ненапряженного железобетона на выносливость не уступает по трудоемкости расчёту на прочность; на номограмме же это самый простой случай, так как линии изменения напряжений ГС и ГБ известны заранее.
Для предварительно напряженных конструкций потребуется вычисление установившихся напряжений в арматуре и бетоне, а также вычисление отношения этих напряжений к расчетным сопротивлениям.
Как правило, вычисление установившихся напряжений в арматуре и бетоне производится при вычислении потерь предварительного напряжения в арматуре. Эти данные следует использовать
' „ (Т., (Тл
При вычислении отношении и ~ .
Ка Кб
По данным этих отношений находим соответствующие наклонные линии для сжатого и растянутого бетона по оси ГА и арматуры по оси ГМ.
Проведя вертикальную прямую из значения минимальной относительной нагрузки на пересечении с найденными линиями, получаем соответствующие относительные напряжения в арматуре и бетоне для этой нагрузки. Переносим значения относительных минимальных напряжений на номограммы расчетных характеристик бетона и арматуры по выносливости и получаем величину допустимой расчетной амплитуды, максимальное значение которой сносим на среднюю часть,
Если действующая максимальная нагрузка будет меньше полученной, то сечение удовлетворяет требованиям по выносливости; в противном случае требуется пересчет.
Для иллюстрации пользования номограммой проверим выносливость преднапряженной балки, пример расчета которой содержится в работе [5]. Пользование номограммой пояснено на фиг. 19, б.
По данным указанного примера Мрасч = 1210 тм, Мт-т — = 288,4 тм, Mmax = 610,7 тм.
Расчетное сопротивление арматуры из гладкой высокопрочной проволоки диаметром 5 мм Ra = 9500 кГ/см2.
Установившееся напряжение в арматуре аа = 7415 кГ/см2.
Установившееся напряжение сжатия в бетоне: верхней грани в% = 0,2 кГ/см2, нижней — eg = 164 кГ/см2.
Расчетное сопротивление бетона марки «400» на сжатие при изгибе Ru = 215 кГ/см2.
Находим линии, по которым будет происходить изменение напряжений с ростом нагрузки, для чего вычисляем относительное напряжение сжатия бетона верхней и нижней грани:
К» = т =0,76; к°б = Ш = °-00093-
В данном примере линия изменения напряжения в крайнем волокне сжатой нижней грани практически совпадает с диагональю Г Б. Это совпадение, конечно, случайное. Для верхней грани эта линия расположена параллельно АР и исходит из ординаты со значением 0,76 на оси АГ.
Относительное напряжение в арматуре
^ = ЙЙ =
Находим также отношения
Xм. - — 0 24
J\min — 1210 —
И
Кя _ 610,7 _ q
Атах — 2210 —
Для арматуры линия изменения напряжения будет исходить из ординаты со значением 0,78 на оси ГМ. Затем откладываем величину 0,24 по оси АБ и проводим вертикальную линию до пересечения с линией для растянутого бетона (точка с) с линией для сжатого бетона (точка Ь) и с линией для арматуры (точка а). Сносим полученные значения на диаграммы выносливости арматуры и бетона по прямым bblt aalt ссх. Расстояния между точками ах и а2, Ъх и Ь2, сх и с2 показывают максимально допустимые амплитуды относительных напряжений в бетоне и арматуре при изменении момента от минимума до максимума. Если снести величины полученных напряжений на исходные линии, то можно получить относительное допустимое значение максимальных моментов: по рас-
Г м'] \м'б\
Тянутому бетону —- = 0,72, по сжатому бетону -——-
Мрасч Мрасч
= 0,85. По арматуре это отношение равно единице, так как точка а3 совпадает с точкой с.
Условие трещиностойкости по нормальному сечению при воздействии повторной нагрузки запишется так:
Mmax < [Мт]
Мрасч ' Мрасч
Условия прочности по сжатому бетону и растянутой арматуре соответственно
Mmax < М'б и Мтах < К Мрасч Мрасч Мрасч Мрасч
Для нашего случая сечение, рассчитанное на статическую нагрузку, удовлетворяет требованиям по выносливости арматуры и бетона и трещиностойкости растянутой зоны.
Для проверки выносливости можно обойтись и без определения отношений моментов. Для этого надо отложить по оси нагрузок (ось А Б) относительное значение максимального момента (в нашем случае величину 0,505), а затем перенести точки пересечения вертикальной прямой с соответствующими наклонными линиями изменения напряжений (точки с, f и d) на правую и левую часть номограммы и убедиться, лежат ли действующие относительные амплитуды внутри максимально допустимых амплитуд или, иными словами, лежит ли отрезок b1f1 внутри отрезка bотрезок с1е1 внутри CiC2 и отрезок aidx внутри ахаг. Если действующая относительная амплитуда не превышает допустимую, то сечение удовлетворяет требованиям по выносливости.
Для иллюстрации случая, когда сечение не удовлетворяет требованиям на выносливость после статического расчета, воспользуемся примером из той же работы [5]. По данным примера
МраСч — 141,7 тм\ M'min = 18,13 тм; Мтах=Ш>56 тм.
Конструкция из обычного железобетона с арматурой из стали марки Ст. 5 (класс А-11). Сечение было подобрано по расчетному моменту 141,7 тм, процент армирования (ц = 1,43%). Проверим его на выносливость по номограмме. Фактические соотношения моментов будут
V* 18,13 п 1/-М 111,56 П7П Amin — щ - j — >ЛЮ, Amax — j^j 7 — и,/».
Линий, соответствующих этому примеру, на номограмме нет, но читатель легко может провести их самостоятельно. По номограмме находим, что сечение не проходит по выносливости арматуры. Аналогично это было установлено путем вычислений и в данном примере. После пересчета процент армирования по выносливости оказался равным 1,59%, расчетный момент внешних сил остался тем же, т. е. равным 141,7 тм, а расчетный момент внутренних сил увеличился до 158 тм.
Находим новые значения К:
Км — 18'13 _ п 11 с. vM - 111,56 _ п 71 Amin — jgg — "liiJ, Лтах jgg — і -
Смотрим по номограмме: сечение проходит по величине действующей амплитуды моментов. Следует отметить, что величина необходимого момента внутренних сил может быть найдена делением величины максимального момента (111,56 тм) на полученное по номограмме отношение допустимого максимального момента к расчетному, т. е. на 0,72.
При этом получим
111,56 1СС 0 у2 = 155 тм.
По полученному расчетному моменту подбираем сечение статическим расчетом, увеличив соответственно количество арматуры.
Из сказанного вытекает, что проверка выносливости по номограмме должна предшествовать расчету на прочность для ненапряженных железобетонных конструкций. Зная расчетные моменты статической нагрузки Мрасч и моменты по выносливости Мтщ и Мтах, находим их соотношение и проверяем по номограмме, не превышает ли полученная амплитуда допускаемую. Если действующая относительная амплитуда меньше допускаемой (по бетону и арматуре), то сечение подбирается по Мрасч. Если же фактическая относительная амплитуда больше допускаемой, то вычисляется необходимый момент внутренних сил, по которому и ведется подбор сечения при статическом расчете. Полученное сечение будет удовлетворять и требованиям по выносливости.
Для предварительно напряженных конструкций, однако, потребуется сначала определить установившиеся напряжения в бетоне и арматуре, найти соответствующие им линии изменения напряжений и затем поступать, как было проделано в примере.
Для случая центрального сжатия ход рассуждений остается таким же, но вместо величин моментов надо брать соответствующие величины продольных сил.
Номограмма не охватывает проверку по выносливости вне- центренно сжатых и внецентренно растянутых элементов, а также проверку по выносливости по главным растягивающим напряжениям для всех элементов.
По номограмме также не предусмотрена проверка по выносливости при действии знакопеременной нагрузки. Однако это не трудно сделать, еслй построить диаграмму Гудмана для арматуры и при значениях Q <0.