Тип длинноцепной разветвленности ПЭВД
Различают три основных типа длинноцепной разветвленности полимеров: „звезда", „гребень" и хаотическая разветвленность. Исходя из одинаковой вероятности передачи цепи на любой вторичный углеродный
атом макромолекулы или макрорадикала, следует ожидать, что ДЦР ПЭВД относится к хаотическому типу со случайным расположением узлов ветвления. При этом узлы ветвления являются трифункциональ - ными, так как нестабильность третичного макрорадикала исключает возможность существования тетрафункциональных узлов.
Именно такого взгляда на ДЦР ПЭВД и придерживаются обычно исследователи при определении структуры макромолекул ПЭВД по данным исследования полимера в разбавленных растворах. Однако в ряде работ [105—107] предложены методы расчета молекулярных характеристик ПЭВД, основанные на модели, подразумевающей гребнеобразное строение макромолекул, что существенно упростило расчеты. Подобное представление о структуре полиэтилена требует специального доказательства. В работе [108] показано, что анализ зависимости [т?] р — М в широком интервале значений М фракций полидисперсного разветвленного полимера, характеризующегося монотонной зависимостью т от М, может дать сведения о типе разветвленной структуры. Поскольку ПЭВД с достаточно хорошим приближением может быть отнесен к таким полимерам, к нему было применено предложенное рассмотрение и показано, что преобладающим типом ДЦР ПЭВД является хаотическая разветвленность.
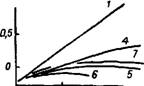
На рис. 7.8 приведены рассчитанные зависимости [jj] - М для изомеров полиэтилена линейной и разветвленной структуры. Расчеты были
|
|
|
1,0 |
|
X о |
|
-0,5 |
|
5 |
|
Рис. 7.8. Зависимость lg [17] от IgM для разветвленных изомеров полиэтилена: |
|
Jj-f г»,т а |
|
' -
|
|
6 |
|
1ft 6
|
|
Г" |
А — „гребень"; б, в — хаотическая разветвленность по [101, 102} и [109] соответственно: 1 — линейный
Изомер (ПЭНД); 2 - ЛГ = 4-10"5; 3 - ЛГ=10~4; 4, 5, 6 - /0 = 100, а = = 1,1, 1,0, 0,9 соответственно; 7 — /0 = 130, а= 1,0
_!____ Рис. 7.9. Зависимость Igfa] от lgМ
В ЩМ для фракций трех образцов ПЭВД, синтезированных в реакторе труб
Чатого типа
Выполнены как с помощью „традиционных" моделей [101, 102] хаотически и гребнеобразно разветвленных макромолекул со статистическим распределением узлов ветвления, для которых функция g(m) описывается уравнениями (7.1).и (29) [102] в первом случае и (31) [102] во втором, так и с помощью предложенных в работах [109] моделей образования и роста разветвленных макромолекул, которые основаны на учете кинетического характера формирования структуры хаотически разветвленных макромолекул в процессах радикальной полимеризации и принципиально отличаются от „традиционных" моделей.
Связь между тиМв случае первых моделей была задана в виде:
Т=КМР,
Ще К — const > 0; /3 = const >0.
В последних моделях длина ветвей макромолекулы может меняться в ходе процесса формирования разветвленной макромолекулы в зависимости от физико-химических и технологических условий полимеризации по закону:
Где la, lm ~ длины начальной ветви и ветвн, выросшей после m-го акта разветвления соответственно; а = const >0.
При этом тиМсвязаны соотношениями:
Т = (М-М0)/М0, а = 1; т =ln [1 + (а - \)М/М0 ]/1па, а#1.
Расчеты соответствуют измерениям [т?] в декалине при температуре 135 °С, для линейного изомера выполняется соотношение [т?] л = = 3,8 • Ю-4 Л/0'74 дл/г.
Как видно из рис. 7.8, характер кривых для различных типов развет - вленности весьма различен. При этом вид графика для хаотически разветвленного полимера существенно отличен от такового для линейного полимера, что позволяет установить этот тип разветвленности по данным [т?] - М даже без предварительного анализа линейного полимера. В случае „гребня" нет столь характерного отличия от линейного полимера и для обнаружения разветвленности в этом случае требуется исследование и линейного аналога.
На рис. 7.9 приведены зависимости [rj] - М по результатам исследования фракций ПЭВД образцов, синтезированных в реакторах трубчатого типа. Сопоставление рис. 7.8 и 7.9 показывает, что вид зависимости [т?] - М для фракций ПЭВД во всех случаях гораздо более соответствует виду кривых, рассчитанных для модели хаотической разветвленности, чем для „гребня".