Технология МАЛОГАБАРИТНЫХ ГИРОМОТОРОВ
ДИНАМИЧЕСКОЕ УРАВНОВЕШИВАНИЕ
Динамическое уравновешивание цилиндрических деталей, какими являются и роторы гиромоторов, основано на положении, установленном акад. А. Н. Крыловым, показавшим, что уравнове
|
|
Шивание любого ротора может быть достигнуто присоединением к нему (или удалением от него) двух масс, расположенных в произвольно выбранных плоскостях, перпендикулярных оси вращения ротора. На использовании этого положения основаны все существующие в настоящее время методы уравновешивания роторов.
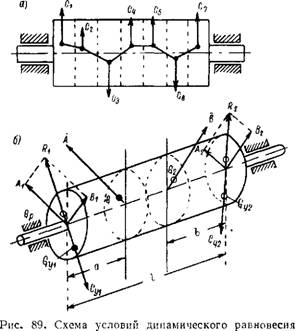
Рассмотрим изображенный на рис 89, а и б цилиндр, разделенный на несколько элементарных дисков. Диски неуравновешены по отношению к оси вращения в разных местах цилиндра и образуют некоторую ломаную линию приложения результирующих сил инерции каждого диска. При вращении цилиндра вследствие сил инерции каждого диска появятся центробежные силы Сг, С2, С3, которые вызовут дополнительные вредные силы в подшипниках. Необходимо выяснить условия, при которых центробежные силы дисков могут быть уравновешены и не будут вредно влиять на подшипники.
Первоначально упростим задачу, предположив, что цилиндр жесткий, недеформирующийся и имеет два неуравновешенных груза, расположенных на разных расстояниях от торцов, направленных в разные стороны и при вращении создающих центробежные силы А и В.
Эти центробежные силы могут быть соответствующим образом разложены на две составляющие и перенесены на торцовые плоскости цилиндра, а именно:
/ 2 / і - і
Где а — расстояние от одного торца цилиндра до места приложения вектора центробежной силы А; b — расстояние от второго торца цилиндра до места приложения вектора центробежной силы В; I — расстояние между подшипниками.
Направление составляющих векторов Аг и А2 и векторов Bi и В2 то же. что и направление векторов сил А и В. Таким образом, разложением получаем радиальные силы А1 и Вг в плоскости первого торца и Л2 и В2 в плоскости второго торца цилиндра. Геометрически складывая эти силы, получаем две результирующие силы и R2, расположенные в двух торцовых плоскостях и одинаковые по величине и направлению с центробежными силами А я В.
Следовательно, если бы цилиндр имел не две неуравновешенные центробежные силы, а несколько, то путем аналогичного разложения этих сил на силы, лежащие в торцовых плоскостях цилиндра, все их можно привести к двум равным неуравновешенным центробежным силам, приложенным в любых двух несовпадающих плоскостях, перпендикулярных оси вращения цилиндра.
Для достижения динамического равновесия необходимо к диаметрально противоположным силам Rx и R.2 приложить в этих плоскостях уравновешивающие грузы Gyl и Gy2, создающие центробежные силы Су1 и Су2, равные по величине и противоположно направленные результирующим силам Rt и R2.
Задачей динамического уравновешивания цилиндрических тел и является определение величины и местоположения уравновешивающих грузов, приложение которых создало бы центробежные силы,
равные по величине и противоположно направленные неуравновешенным силам, вызывающим колебания цилиндра при вращении и вредные нагрузки на подшипники. При равенстве этих сил вынужденные колебания цилиндра прекратятся.
При динамической балансировке цилиндр уравновешивают сначала с одного, а затем с другого торца. Точность динамической балансировки значительно выше, чем статической.
Для точного определения при динамической балансировке роторов гиромоторов величины уравновешивающего груза и его местоположения существуют разнообразные конструкции балансировочных машин, основанных на разных принципах действия.