СТАЦИОНАРНОЕ СОСТОЯНИЕ ЛИНЕЙНОЙ СИСТЕМЫ
Если на термодинамическую систему наложены ограничения, фиксирующие постоянные значения некоторой совокупности обобщенных сил, причем остальные обобщенные силы могут меняться, система придет в стационарное, хотя и неравновесное состояние. Очевидно, что такая ситуация может осуществиться только в открытой системе. Итак, если Х\, Х2, ..., Хк постоянны, a Xk+i, Xh+2 XN свободно изменяются, то
J і — 0 для і > k, J і-Ф0 для і ^ k.
Энтропия такой системы не достигает максимума, и функция диссипации отлична от нуля. Допустим, что система обменивается с окружающей средой и веществом, и энергией, но масса ее остается постоянной. В системе имеются тепловой поток /т и поток вещества /м, причем последний равен нулю:
А = JTXT + JUXU (2.50)
И
H — L\\XT -f - I (2 51)
Лі = L2\Xt + L22JM = 0. J
Считая фиксированной силу Хт (скажем, это фиксированная разность температур), имеем
А = LnXl + (L,2 + L2i) ХТХМ + L22X\■ (2.52)
Дифференцируем это выражение по Х„ при Хт = const: - щ - = 2L22Xu - f- (Ll2 - f- L2i) X?.
Если система близка к равновесию и выполняется теорема Он- загера, то Li2 = L2i и
-§- = 2(Ll2XT + L22XM) = 2JM = 0. (2.53)
Следовательно, в стационарном состоянии, близком к равновесию, продукция энтропии а минимальна (действительно, cfo/dXu = L22 > О). Это — теорема Пригожина [2, 10]. Она непосредственно связана с теоремой Онзагера и справедлива лишь в пределах применимости линейной термодинамики. Коэффициенты La здесь независимы от X,.
Если Хт также может изменяться произвольным образом, то /т = /м = 0, а обращается в нуль и система достигает равновесия.
Рассмотрим открытую химическую систему. Вещество А поступает в нее извне, претерпевает ряд последовательных реакций внутри системы, и конечный продукт реакции F покидает систему [2]:
—>• А В С —>• . .. F -—*-.
Кинетические уравнения имеют вид
DnA dexnA dnB dnF dex"F. ,0 c ,,
~dF ~ dt Vu - dT=°i-02. ■■■. - dT=—dn + vr' (2-54)
Где производные с индексом «ех» характеризуют обмен с внешней средой.
В стационарном состоянии все скорости выравниваются:
DexnA dexnF /0
-g— = Vi = и2 = ... = vr = JJ- = V, (2.55)
И содержание всех реагентов в системе постоянно: Пр = 0 (р = А, В, .... F).
Имеем
= ^ - Т + Е + * ^ > 0. (2-56) р-1
Где
Верхний индекс (1) относится к системе, а (2) — к окружающей среде. В стационарном состоянии
+ — = >0, (2.57)
Где соответствует глобальному (суммарному) процессу
Д(2)_>.р(2) q другой стороны, в линейной области
Г+2 г+2
А = Е Z >0- (2.58)
Р-1 р'=1
Определение минимума (2.58) при данном значении суммарного сродства s4- проводим с помощью множителей Лагранжа g. Продифференцируем функцию
Р р' р
По зФр/Т и приравняем производную нулю. Имеем
D(stJT) = L-i ~~Т 2g = 0. р'
Скорость Op = Lpp' (sЈP'/T) = g== const. Следовательно, усло - p'
Вие постоянства скоростей эквивалентно минимуму производства энтропии и действительно означает стационарность.
Определим теперь условия стабильности стационарного состояния. Условие минимума а дает некий критерий эволюции, показывая, что система необходимым образом переходит в стационарное неравновесное состояние из любого близкого к нему состояния. Без ограничения общности рассмотрим случай двух сопряженных химических реакций [2]:
А = LU (*)2 + 2L12 + L* ( * )' > (2-59)
Вычислим о, считая коэффициенты Ь\2 постоянными: т а = {L,, — + Ц2 - у-J —Tt— +
+ ^12 т +L22 т J dt і rfi +y2 57 • (2.b0)
В замкнутой системе и ^г зависят от координат реакций |ь а также от давления и температуры, которые будем считать постоянными. Тогда можно написать
Как указывалось выше, сродство зФ есть производная от свободной энергии системы по координате соответствующей реакции, взятая со знаком минус, т. е.
<2Л0>
„ дЛ\ ds4->
Следовательно, д^ = , и мы получаем
1 . 1 ( дЖх „ 0 dsЈ 1 (9^2 .Л ^ Г> /Г.
Та=Т І ИГ + 2 -5ІГ У1У2 + Ф < (2-62)
Величина эта отрицательна, так как величины убывают сростом gj. В замкнутой системе продукция энтропии может только убывать во времени.
В открытой системе к выражению (2.62) добавляется выражение, описывающее обмен веществом с внешней средой:
1 1 1 v-> Ґ ds$i dsf-o \ dexnv
Y
Здесь первый член всегда отрицателен, знак второго зависит от конкретной ситуации. Внутренние необратимые процессы всегда понижают скорость продукции энтропии. Из неравенства (2.62) следует, что если система достигла состояния с минимумом продукции энтропии, то она не может покинуть его спонтанно.
Дифференциал функции диссипации можно представить в виде
Da = d, a + dxa = Z Xt dJt + Z /г dXt. (2.64)
І і
При вычислении da/dt по формуле (2.60) мы ограничивались dxojdt, учитывая изменение во времени лишь для сил X,- (т. е.
З М. В. Волькепштейн
для зФііТ). Однако вследствие условия Онзагера L\2 = L2X в линейной области dxa = dja, что нетрудно проверить. Тем самым, dxa есть полный дифференциал;
J 11 , dxa do
В стационарном состоянии, как мы видели, а, < 0, т. е. dxa < О, da < 0. Соответственно вариационное условие стабильности стационарного состояния состоит в том, что
Бст = 26хсг > 0. (2.65)
Знак вариации а противоположен знаку дифференциала — любая флуктуация может вызвать лишь избыточную продукцию энтропии. Допустим, что /м = 0 в стационарном состоянии
С фиксированными силами Xi Xh
И нефиксированными Xh+\, ..., Хг. При флуктуации 8ХМ
Имеем / м = L„M6XM,
Где LMM > 0 и
6xo = JM6X№ = Lm(6XMf>0.
Для химической системы это условие запишется в виде
TbxG^lLVi 6.5^ > 0. і
В стационарном состоянии (индекс «st») і
Если все независимы. Этого всегда можно достичь образованием подходящих линейных комбинаций скоростей и значений сродства индивидуальных реакций. Следовательно, можно положить стационарные значения О;1 равными нулю. Тогда получаем
О* = vt + Ч = бг, г>
И условие стабильности принимает вид
ТЬха = S bvi ЬзФі > 0. (2.66)
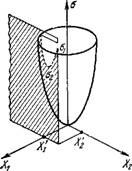
Рис. 2.]. Схема, поясняющая поведение стационарной линейной системы.
Как мы видели (см., например, (2.52)), а выражается квадратичной функцией от X. Представим это схематическим рис. 2.1 [8] для случая двух сил X] и Х2. Если при X] == const Х2 может варьировать, точка, изображающая а, будет двигаться по параболе, получаемой пересечением поверхности cr(Xi, X2) пло
скостью Xi = const, пока она не достигнет минимума Ог. Если упразднены все ограничения, а будет двигаться по поверхности до равновесной точки о = 0.
Возвращение флуктуировавшей линейной системы в стационарное состояние, достаточно близкое к равновесию, происходит экспоненциально, без осцилляций:
As = I (0 - г1 = (I (0) - Ist) ехр (- Их), (2.67)
Где gst — стационарное значение координаты реакции, т — время релаксации.
§ 2.4. СОПРЯЖЕНИЕ ХИМИЧЕСКИХ РЕАКЦИЙ С ПРОЦЕССАМИ ДИФФУЗИИ
Организм, клетка — химические машины, функционирующие в результате протекания химических реакций и переноса вещества между клеткой и окружающей средой. Этот перенос имеет направленный характер, он происходит в направлении, нормальном к клеточной мембране. Соответственно поток вещества (диффузия) есть вектор.
Перенос вещества и биохимические реакции взаимосвязаны в процессах метаболизма. Эта взаимосвязь определяет, в частности, активный транспорт сквозь мембраны, рассматриваемый в следующей главе. Здесь нас интересует феноменологическое описание взаимосвязи, т. е. сопряжения химических реакций и транспорта вещества (диффузии).
Как уже сказано выше (см. стр. 57), прямое сопряжение скалярного и векторного процессов невозможно в изотропной системе в силу принципа Кюри. Невозможно оно и в анизотропных центросимметричных системах. Однако биологические системы, в которых сопрягаются диффузия и химические реакции, а именно, мембраны, построены из хиральных молекул, лишенных центра и плоскости симметрии. В таких системах в принципе возможно прямое сопряжение, и векторные коэффициенты Lsv = Lvs не обязаны равняться нулю (см. стр. 57). Теория прямого сопряжения диффузионных и химических процессов в мембранах, непосредственно учитывающая хиральность среды, пока ке развита. Можно представить себе, например, транспорт неких участников реакции вдоль винтового канала, в котором расположены симметричные реакционные центры. Тогда течение реакции будет различным для веществ, поступающих с разных сторон канала. К тому же результату приводит рассмотрение модели, состоящей из симметричных каналов, в которых находятся асимметричные реакционные центры. Однако пока нет оснований утверждать, что эти эффекты значительны. Взаимосвязь химических реакций и транспорта веществ может определяться не прямым, но косвенным сопряжением, возникающим в
условиях стационарности. В целом проблема требует дальнейших исследований.
В стационарном состоянии возникает связь между необратимыми процессами, которые не сопряжены непосредственно феноменологическими коэффициентами. Вернемся к примеру, рассмотренному на стр. 63. Наряду с веществами, участвующими в реакции
(2.68)
•^хим
Будем вводить в систему инертное вещество Q, в реакции не участвующее [2]. Его транспорт сопряжен, однако, с транспортом вещества А. Тогда
|
Т |
DexnA |
|
Dt |
|
|
Т |
DexnQ |
|
Dt |
|
|
Т |
DexnF |
|
Dt ~ |
V — L*
Последнее уравнение относится к химической реакции А—► F. Из условий стационарности находим
DexnA dnF dexnP dnQ dexnQ
~dF== dt w = 0, - dF = —dT + v = °> = ^
(2.69)
= 0.
Или
DexnA _ dexn p dexnQ
Dt dt ' dt Следовательно,
^11 — (^-12/^22) j ^F Ll\ — (^12/^22)
(2.70)
Сродство st-q инертной компоненты отлично от нуля и пропорционально скорости химической реакции, в которой вещество не участвует. Вследствие этой реакции возникает разность концентраций Q внутри и вне системы
C$/c<$ = Kexp(-stQ/RT). (2.71)
Тем самым реализуется косвенное сопряжение транспорта инертного вещества и химической реакции.
Напишем функцию диссипации для системы, в которой имеется транспорт и химическая реакция (для транспорта обобщенная сила выражается через градиент химического
потенциала |іі):
ОТ = Z /jV (- ц,) - О £ V,(2.72)
/ »
И рассмотрим косвенное сопряжение в общем виде [11]. Условие непрерывности для 1-й компоненты есть
^ = - Wi + VtV. (2.73)
Условие стационарности, т. е. постоянство концентрации выразится как
V7Ј = v, o. (2.74) Подставляя в (2.72) это выражение, находим
AT = - Vj^Jtiit. (2.75)
І
Проинтегрируем а для случая одномерного потока вдоль оси х. Получаем полную диссипацию на единицу площади
Ах
О** a dx = - у £ (/, (0) Hi (0) - J і (Ах) Ні (Ах)). (2.76) 0 і Аналогичное интегрирование дает (ср. (2.74))
&х Ах
J 4г dx = - У< = v< J у dx = (2.77)
О о
Из двух последних уравнений следует, что
То* = Z Jt (0) [ц, (0) - щ (Ах)} + 4им Z [- (Л*)], і І
Или (2.78)
Tatot = Z J і (А*) [Ц, (0) - (Ал:)] + 4°„м Z [- (0)].
Г г
Суммы в последних членах правых частей (2.78) выражают значения сродства реакции при х = Ах и х = 0 для проникающих в систему (в мембрану) компонентов. Переходя к феноменологическим уравнениям, напишем
/tot _ у, О А, г о <£АХ\ (2-79)
•«хим — Zj lxhm, і ^M-t ^хим»**- , 1 I '
Ji(Ax) = Z^tk^k + Lt\lltis^0, - J •С„ = Z £хиы, і Ар, г + ( (2'80)
В макроскопических (проинтегрированных) выражениях появились перекрестные макроскопические коэффициенты Li, хим ИЛИ Li,*xим - Симметричны ли оии? В локальных (неиитегрирован - ных) выражениях перекрестных коэффициентов нет, так как наша система изотропна и принцип Кюри справедлив. Иными словами,
/» = £ w- (ij), ]
K [ (2.81)
Где lih — локальные феноменологические коэффициенты. То же относится к обратным выражениям
V(-її,) = !>,*/*, )
" , \ (2.82) & = rxhmv = т— о. )
'хим '
Установим связь между локальными и макроскопическими коэффициентами. Применяя к первому уравнению (2.82) оператор V, получим
V2(-n<)=Er<Jkv/)k.
K
Подставляя условие стационарности (2.74), находим
V2 (- Щ) = (I rik) о == (/хим S vkrik) а. (2.83)
Умножим обе части этого уравнения на v,- и просуммируем по г.
Так как s4- = — 2 получаем і
£ v4V» (- (і,) = V2^ = f /хим Z vm») (2.84)
T \ i, k J
Мы получили дифференциальное уравнение для Коэффициент, стоящий при бФ, имеет размерность см-2. Обозначим его через Х~2 (X — длина релаксации). Тогда
Я,2?2^ = а. (2.84а)
Решение этого уравнения имеет вид
StAx sh (х/Х) + sh [(Ад; - ж)Д] ' ' = sh (Дх/А) • (2-85)
Для перехода к макроскопическим выражениям нужно проинтегрировать локальные соотношения. Интегрирование (2.74) от
О до произвольной точки х дает
X X
\чгйх = 1і W - 7< = S * dx•
О о
Подставляя сюда (2.85) и проводя интегрирование, получаем
Уw=+ infer {^ (ch т - 1)-
С другой стороны, согласно (2.81), левая часть этого выражения равна
К
Подставим это выражение в (2.86) и проинтегрируем от 0 до Ах. Так как
Ах
С dp,
~ ) 1Г dx = ^ ~ ^ =
О
И
- а0 = - Z v, n, (А*) + Z V, H, (0) = Z V; A|i„
То в результате интегрирования имеем
J°tAx = Z {lik + v;vftAJXHM (A* cth (Аф) - Щ A|xft -
- (vЈЯ/хим A* th (Ax/21)) ^*. (2.87)
Разделим (2.87) на Ax и получим макроскопические феноменологические выражения. Введем обозначения
Я/хим (cth (Ах/Х) — К/Ах) = а, А/хим th (Ах/2Х) = р.
То. гда окончательно находим
H (0) = £ Ш + v'vfta) ~ Vi№Ax, (2.88) k
Что совпадает с (2.79), причем
L°ik = "fe + v<v*a' L° хим = ~ ViP - (2.89)
Вычисление /хим дает
Ах Ах
/хим = ^ /ХИм dx = /хим ^ s4- dx =
О о
= Мхим + th (Ах/2Я) = - z ViP + 2р^д*. (2.90)
Сравнивая (2.90) со вторым уравнением (2.79), находим
Ьхим = Ьг, ХИМ = v, P, L°им = 2р. (2.91)
Таким образом, макроскопические коэффициенты, характеризующие косвенное сопряжение диффузионных потоков и химической реакции, выражены через микроскопические коэффициенты. Соотношения симметрии Онзагера сохраняются. Отличие от нуля макроскопических коэффициентов определяется в случае изотропной системы условиями стационарности. Как мы увидим, косвенное сопряжение играет существенную роль в теории активного мембранного транспорта (см. гл. 3 и 6). В гл. 3 изложено также применение описанной теории косвенного сопряжения при рассмотрении так называемого облегченного транспорта, происходящего с участием молекул-переносчиков.
Косвенное сопряжение химических реакций и теплового потока рассмотрено Де Гроотом [4, 5].