АППАРАТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ
Скорость процесса сушки
Состояние влаги в материале. Протекание процесса сушки в значительной мере зависит от характера связи испаряемой влаги с материалом; жидкость может быть соединена с материалом силами сцепления, капиллярными силами и др.
Жидкость, соединенная с материалом силами сцепления, находится главным образом на поверхности тела; при ее испарении каждой температуре соответствует вполне определенное давление пара, равное упругости насыщенного пара жидкости при данной температуре.
Некоторая часть жидкости, заключенной в материале (например, песке, растительных волокнах), может быть связана с ним капиллярными силами. В этом случае для испарения жидкости необходимо, чтобы температура влаги была несколько выше температуры кипения ее при данном давлении.
Обычно различают два вида влаги, заключенной в материале: свободную и гигроскопическую.
Скорость испарения свободной влаги определяется по закону испарения со свободной поверхности, т. е. давление паров над поверхностью материала при бесконечно малой скорости сушки равно давлению насыщенного пара при той же температуре.
Влага, при наличии которой парциальное давление над высушиваемым материалом становится меньше давления насыщенного пара при той же температуре, называется гигроскопической. Гигроскопическая влага более прочно связана с материалом и удалить ее трудно.
Свободная влага переходит из материала в окружающую среду, как было указано выше, в том случае, когда давление пара над поверхностью влажного материала больше его парциального давления в окру жающей среде, т. е. РН>РП. Процесс сушки будет, очевидно, протекать до того момента, когда давление пара над материалом станет равным давлению пара в воздухе, т. е. до РИ=Р„.
Влажность тонкого слоя материала, при которой устанавливается равновесие между давлением пара на поверхности материала и парциальным давлением пара в окружающем воздухе (газе), называется ра вновесной или устойчивой влажностью.
Каждый материал можно высушить только до равновесной влажности, которая зависит от состояния окружающей среды (ее температуры и относительной влажности).
При наличии в материале гигроскопической влаги РН<РП происходит обратный сушке процесс перемещения влаги из окружающей среды к гигроскопическому материалу, т. е. процесс увлажнения материала или поглощения (сорбции) влаги из окружающего воздуха.
Гигроскопический материал будет поглощать влагу из воздуха до достижения равновесной влажности, которая для многих материалов отлична от равновесной влажности при сушке. Как видно из рис. 466, значение равновесной влажности материала является промежуточным между
Постоянными величинами конечной влажности при сушке и при увлажнении материала.
Таким образом, когда имеется разность парциальных давлений пара над материалом и в воздухе (газе), влага испаряется с поверхности материала. Вследствие этого воз - 3 никает разность между концентрациями / влаги внутри материала и на его поверхности и происходит диффузия влаги к поверхности материала. Процессы испарения и ------------------- диффузии хотя и протекают совместно, но в
Рис. 466. График изменения неодинаковой степени влияют во времени
Влажности во времени: на процесс сушки, /-при сушке; 2—При поглощении При раССМОТрвНИИ КИНЄТИКИ СуШКИ
Влаги из воздуха^ам^-равновес- GQJlee Целесообразно ВЬфажаТЬ ВЛаЖНОСТЬ ВЫ"
Сушиваемого материала в долях к абсолютно сухому материалу, т. е. в единицах абсолютного влагосодержания. Связь между относительным и абсолютным влагосодержанием материала выразится равенством
C = (3-359>
Где с—абсолютное влагосодержание материала; W—влажность материала в %.
Общие понятия о скорости сушки. Скорость сушки определяется W
Количеством влаги в кгс, удаляемым с 1 м2 поверхности высушиваемого материала в час, и выражается в дифференциальной форме следующим образом:
U —кгс/м2 -час (3—360)
Где F—общая поверхность высушиваемого материала в м2\ Т—длительность сушки в часах.
При известной скорости сушки общая ее продолжительность в часах выразится равенством
Т = °с(с^~ск) (3—361)
Где, кроме величин, обозначенных выше:
Gc—количество абсолютно сухого вещества в высушиваемом материале в кгс\
Си и ск—начальное и конечное влагосодержание высушиваемого материала в кгс/кгс абсолютно сухого вещества. Пользуясь уравнением (3—361), можно легко найти продолжительность сушки, если известна скорость сушки U. Однако скорость сушки в течение всего процесса непрерывно изменяется, уменьшаясь с уменьшением влагосодержания высушиваемого материала, причем в большинстве случаев влажные материалы отдают около 90% своей влаги в первую' половину общего времени сушки, а остальные 10%—во вторую.
При расчете сушилок необходимо, таким образом, знать функциональную зависимость скорости сушки от времени, т. е. кривую скорости сушки. Эта зависимость очень сложна, и методы определения ее аналитическим путем еще не найдены.
Практически приходится определять зависимость скорости сушки от времени (строить кривые скорости сушки) путем экспериментального исследования режима процессов сушки с последующей графической обработкой опытных данных в виде кривых в координатах: время сушки— влажность материала при определенных условиях (температура, скорость воздуха и его влагосодержание, толщина слоя материала).
|
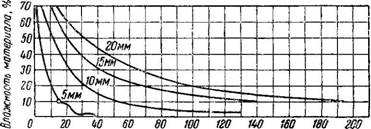
Время, часы Рис. 467. Кривые скорости сушки плиток клея разной толщины. |
На рис. 467 приведены кривые сушки плиток клея разной толщины. По этим кривым можно найти продолжительность сушки для заданных условий. Так, если сушатся плитки клея толщиной 10 мм от заданной начальной влажности 60% до конечной влажности 10%, то продолжительность сушки составит <~44 час. Из этих же кривых видно, что в некоторых пределах влажности сушка протекает сравнительно быстро и равномерно, но затем влажность уменьшается настолько медленно, что кривая сушки проходит почти параллельно оси абсцисс.
В связи с тем, что скорость сушки зависит от большого числа факторов, связать которые в одно целое в виде определенной функции практически не представляется возможным, перечислим лишь главнейшие из них:
П р'и рода высушиваемого материала: структура, химический состав, характер связи с влагой и т. д.
Форма высушиваемого материала: размеры кусков, толщина слоя и т. д. При прочих равных условиях можно считать, что скорость сушки пропорциональна отношению поверхности частицы высушиваемого материала к ее объему; чем больше поверхность высушиваемого материала, тем быстрее проходит сушка.
Начальное и конечное влагосодержание материала, а также его критическое влагосодержание (см. ниже), так как от них зависит снижение во времени скорости сушки
Влажность, температура и скорость воздуха. Чем выше температура и скорость воздуха и чем ниже его относиг тельная влажность, тем быстрее протекает сушка. Однако следует учесть, что допустимые температура и скорость сушильного агента зависят от свойств и формы высушиваемого материала (из условий предотвращения разложения и образования корки и т. д.).
Характери условия обтекания материала воздухом. В лучших условиях обтекания и перемешивания частиц материала с воздухом, например при сушке материала во взвешенном состоянии, скорость сушки возрастает по сравнению с сушкой в неподвижном слое.
Сушильный агент. Применение сушильного агента с высокой температурой при непосредственном обогреве дымовыми газами позволяет во многих случаях значительно сократить продолжительность сушки.
Разность температур сушильного агента на входе и выходе из сушилки. Чем меньше температурный перепад, тем выше средняя температура, а следовательно, и скорость сушки.
Конструкция сушилки, поскольку от устройства сушилки зависят многие перечисленные выше факторы.
Равномерность сушки. Этот фактор имеет существенное значение. Если в части материала не достигнуто заданное влагосодержание, то всю партию приходится задерживать в сушилке, что ведет к удлинению процесса сушки и пересушиванию значительной части продукта.
Как видно из приведенного далеко не полного перечня основных факторов, влияющих на длительность сушки, определение последней расчетом настолько сложно, что практически часто исходят только из опытных данных, определенных для каждого конкретного случая.
Однако, несмотря на сложность кинетики сушки, можно с той или иной степенью точности вычислить продолжительность сушки и теоретическим путем.
Зная начальную влажность материала и его первоначальный вес, можно по уменьшению веса материала в процессе сушки судить о его влажности в любой момент. Зависимость средней влажности материала от времени изображается графически так называемой кривой сушки:
W = ' (А)
Вид кривой W=f(т) зависит от режима сушки, т. е. от многочисленных факторов, перечисленных выше.
Изменение средней влажности материала в единицу времени, т. е. скорость ее изменения, может? быть определена как первая производная выражения (А):
= = (Б)
Знак минус указывает, что влажность материала уменьшается во времени. Кривую, изображающую функцию (Б), называют кривой скорости сушки. Ее можно получить графическим построением из кривой сушки.
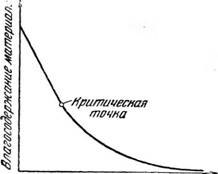
Из диаграммы процесса сушки в виде кривых в координатах: продолжительность сушки—влагосодержание материала, или, скорость сушки— влагосодержание материала (рис. 468 и 469) видно, что кривая скорости сушки имеет резко выраженную точку перегиба, называемую критической точкой процесса сушки. Эта точка соответствует критической средней влажности материала и делит кривую на два отрезка. Первый отрезок представляет собой прямую линию и соответствует п е - риоду постоянной скорости сушки. Второй отрезок представляет собой кривую линию и соответствует периоду падающей скорости сушки. Длительность обоих периодов различна и зависит от свойств материала, его формы и размеров, начальной влажности и других факторов.
В начале сушки скорость внутренней диффузии в теле велика по сравнению со скоростью внешней диффузии и изнутри материала к его поверхности поступает достаточное количество влаги. Поэтому сушка в период постоянной скорости целиком обусловливается скоростью испарения влаги со свободной поверхности высушиваемого материала.
|
/7родо/7Жи/77Є/7М0£ґ/7£ О/ІШі/ Рис 468. Кривая сушки. |
В период постоянной скорости сушки давление пара над поверхностью материала равно его давлению над чистой жидкостью и скорость сушки не зависит ни от толщины слоя материала, ни от его начального влагосодержания, а только от температурного режима сушки, скорости воздуха и его влагосодержания.
В течение второго периода сушки, наоборот, скорость сушки полностью обусловлена скоростью диффузии влаги изнутри материала к его поверхности. Поэтому во второй период скорость сушки зависит от толщины слоя высушиваемого материала и его влагосодержания и практически ке зависит от скорости воздуха и его влажности. В этот период скорость сушки уменьшается и при достижении материалом равновесной влажности равна нулю.
Скорость сушки при постоянном влагосодержании сушильного агента. Первый период. В первый период сушки скорость ее остается постоянной и испарение влаги происходит главным образом со свободной поверхности высушиваемого материала. Количество испаренной влаги dW прямо пропорционально количеству тепла dQ, подводимому к высушиваемому материалу:
DW = BdQ
Где Ь—коэффициент пропорциональности.
По законам теплообмена количество тепла dQ, сообщенное высушиваемому материалу при притоке тепла только от теплоносителя, можно определить как:
DQ — AF(T — 6) Dt Ккал
Где а—коэффициент теплоотдачи в ккал /ж2 - час -°С;
F—поверхность теплообмена, эквивалентная поверхности испарения, в ж2;
T—температура теплоносителя (воздуха) в °С;
6—температура на поверхности высушиваемого материала (температура испарения) в °С; —продолжительность испарения в час.
Подставив значение dQ из последнего уравнения в предыдущее, получим
DW = Bo.F (T — 0) Dz Кгс
Или
DW — KtF (T — 6) Dx Кгс (3—362)
Уравнение (3—362) представляет собой уравнение массопередачи, где Kt~ba—~KoaqVJjHnneHT массопередачи с размерностью
Ш
Ж2* час'°С
И (/—6)—движущая сила процесса сушки.
Отсюда получаем уравнение скорости сушки для первого периода
U = = Kt (/ — 6) кгс/м2 ■ час (3—363)
Из уравнения (3—363) следует, что движущая сила процесса сушки может быть выражена не только разностью влагосодержаний, но и разностью между температурой теплоносителя и температурой поверхности высушиваемого материала.
Обычно движущую силу процесса сушки выражают в виде разности давления насыщенного пара (Рн), соответствующего температуре испарения, и парциального давления пара в протекающем теплоносителе (Рп), заменяя соответственно коэффициенты пропорциональности. Тогда уравнение (3—363) примет вид:
U = -уъ = КР ~ Рп) кгс, м"•час (3~364)
Где Кр—коэффициент массопередачи или скорости испарения.
Если давления Рн и Рп выражены в мм рт. ст., то Кр имеет размерность:
Кгс
М^'часмм рт. ст.
Полученное уравнение является основным законом испарения жидкости со свободной поверхности, предложенным в 1803 г. Дальтоном и подтвержденным многими позднейшими исследованиями.
Коэффициент испарения Кр может быть найден из зависимости
Где Ьг—новый коэффициент пропорциональности, учитывающий переход от разности температур к разности давлений. Отсюда следует, что Кр будет зависеть от тех же факторов, что и коэффициент теплоотдачи а^
При изучении явлений теплоотдачи с приложением теории подобия была найдена зависимость коэффициента теплоотдачи а от различных факторов, определяющих процесс теплообмена. Эта зависимость представлена уравнением в критериальной форме:
Nu = F(Rc. Gr, Pr)
В сушилках воздух обычно проходит через систему при помощи вентилятора, т. е. происходит вынужденное движение теплоносителя, и, следовательно, из уравнения теплообмена в этом случае выпадает критерий Грасгофа (Gr). Тогда
Nu = F1(Re, Рг)
Или в раскрытом виде
Ad ___ л / WYd \п / 3600Cfig
Откуда
А = А0 (Wj)N (Ng)M-NCml1~M Dn~L (3—365)
Уравнение (3—365) может быть значительно^ упрощено, если принять во внимание следующие обстоятельства.
Физические константы для теплоносителя—воздуха: теплопроводность X, теплоемкость с и вязкость {А зависят от температуры воздуха и в обычных пределах температур сушки изменяются незначительно; определяющий размер d является постоянной величиной.
Поэтому, объединив все постоянные величины в одну новую константу А, получим выражение
А = A
Откуда коэффициент испарения: или
Кр — Ах (Wj)N Кгс/м2-час-мм рт. ст. (3—366)
В уравнении (3—366) произведение wj представляет собой весовую скорость воздуха в кгс!'м2- сек.
Таким образом, определение скорости сушки в первый период сводится в основном к подсчету величины коэффициента испарения Кр по уравнению (3—366).
Применив принцип подобия при обработке опытных данных, можно принять следующее значение для коэффициента Кр при условии движения воздуха параллельно поверхности высушиваемого материала:
Кр — 0,0745 (г^т)0»8 кгс/м2-час-мм рт. ст. (3—367)
Где w—скорость движения воздуха в м/сек;
У—уд. вес воздуха в кгс/м*.
Скорость сушки в первый период в этом случае выразится уравнением
U = f^ = 0,0745 (anr)0-8 (Ря - Р„) (3-368)
Из уравнения (3—368) следует, что скорость в первый период сушки зависит только от параметров воздуха, определяемых разностью давлений (Рн—Рп), и от его весовой скорости WJ.
В том случае, когда воздух движется перпендикулярно поверхности испарения, величина коэффициента испарения Кр возрастает примерно вдвое.
На практике при расчете сушилок, для увязки материального баланса процесса сушки с производительностью и определения последней графическим путем, коэффициент испарения относят к разности влаго - содержаний воздуха на поверхности высушиваемого материала (*„) и в воздухе (яп) над высушиваемым материалом.
В соответствии с уравнением (3—326) парциальное давление водяного пара в воздухе Рп=<рРн может быть определено из выражения
а давление пара Рн на поверхности материала при температуре испарения:
Р __ ХЦР
Обычно величины хп и хи малы по сравнению с слагаемым 0,622 и полученные формулы можно упростить:
Р __ хпР
0,622 Х„Р
Н 0,622
Принимая общее давление Р =760 мм рт. ст., получим
|
И |
Р = 760
0,622 760
X»
Н 0,622
Подставив полученные значения Рп и Рн в уравнение (3—364) Дальтона, получим
(х-Х)
~~~ Fdx 0,622
ИЛИ
И = ТЖ = Кх(х«- хп) (3-369)
Где
К-=бЖ2 К^1220 КР
Очевидно, что расчет скорости сушки по уравнениям (3—369) и (3—368) должен дать одинаковые результаты.
Предполагая подобие между температурным полем и полем концентрации пара в воздухе в процессе испарения, можно определить значение коэффициента испарения Кх по величине коэффициента теплоотдачи а из соотношения
= (3—370)
Кх М
Где а—коэффициент теплоотдачи в ккал! м2- час -°С; Кх—коэффициент испарения в кгс'м2-час-Ах; Св—теплоемкость влажного воздуха в ккал! кгс°С.
<а= —----- коэффициент температуропроводности в м2/час;
D—коэффициент диффузии паровоздушной смеси в м2!час.
При испарении воды в воздух отношение теплоемкость
Влажного воздуха св~0,25 и, следовательно, уравнение (3—370) принимает вид
Или
Кх = 4,35а (3—371)
Уравнения (3—369) и (3—371) выражают только приближенные соотношения, поскольку имеющиеся опытные данные по определению коэффициента теплоотдачи а не могут быть перенесены непосредственно на
процессы сушки, протекающие обычно в условиях, отличных от теплообмена.
Поэтому при определении Кх по уравнению (3—371) необходимо тщательно подбирать значение коэффициента а, исходя из того, что условия протекания процесса теплообмена должны быть по возможности наиболее близки к условиям протекания процесса сушки.
|
Fd |
Для того чтобы установить связь между коэффициентом испарения Кх, отнесенным к разности влагосодержания, и коэффициентом испарения Kt, отнесенным к разности температур, достаточно сопоставить уравнения (3—363) и (3—369):
■■Кх —
Откуда получим
К<(і-Щ=Кх{хИ-хП)
Полученное соотношение является безразмерным и удовлетворяется при условии однозначности величин Kt и Кг, а также величин (t—6) и (*„—*!,)•
Таким образом, окончательно устанавливается связь между различными выражениями коэффициента испарения и коэффициентом теплоотдачи
І±Kt = Kx= 1220Кр = 4,35а (3-372)
Соотношение размерностей коэффициентов испарения Kt, Кх и Кр может быть выражено следующим образом:
At Кгс кгс ____ 1220 кгс
Ах м2*час*°С м2*час*Ах м2'час>мм рт. ст.
Преобразование уравнения диффузии совместно с уравнениями гидродинамики и граничных условий на основе принципов подобия приводит к критериям теплового подобия, в которых коэффициент температуропроводности заменяется коэффициентом диффузии влаги в высушиваемом материале.
Второй период. В связи с тем, что имеется мало опытных данных, характеризующих подобие протекания процессов сушки в период уменьшающейся скорости, невозможно обработать эти данные с применением критериев подобия и рекомендовать надежные расчетные формулы. Поэтому приходится применять более доступные, хотя и менее точные пути решения.
Упрощенный метод основан на том, что процесс сушки в период уменьшающейся скорости можно с достаточной степенью точности изобразить прямой линией, соединяющей критическую точку с точкой равновесного влагосодержания материала, как это показано пунктипом на рис. 469.
Можно допустить, что во время второго периода скорость сушки прямо пропорциональна свободному влагосодержанию высушиваемого материала и что движущей силой процесса является разность между
Свободным и равновесным влагосодержанием в любой момент сушки. Эта зависимость может быть выражена уравнением
U = = Кс (с — ср) кгс! ж2 • час (3—37 4>
Где с—влагосодержание материала в любой момент, выраженное в кгс! кгс абсолютно сухого материала; ср—равновесное влагосодержание материала в кгс/кгс абсолютно-
Сухого материала. По уравнению материального баланса
DW = — Gdc
И, следовательно
DW_____ _Gdc_ Jr _ .
Fx F Dx C CV'
После интегрирования в пределах от с0 до с2 и от т=0 до получим
JL In СР — к т
Где с0—критическое влагосодержание;
С2—влагосодержание материала в конце второго периода сушки; с—равновесное влагосодержание; Кс—коэффициент массопередачи в кгс/м2 - час\ т2—продолжительность второго периода в час. Решая последнее уравнение относительно т2, находим продолжительность второго периода сушки:
LncJLZlfp чаСл (3—375)
2 KCF с2
Из уравнения (3—375) может быть также определена скорость сушки первого периода. Согласно кривой, изображенной на рис. 336, скорость сушки в период постоянной скорости равна скорости сушки в критической точке. Следовательно, вместо величины с в уравнение для первого периода должно быть подставлено с0—критическое влагосодержание и тогда
— K (с —с )
Р Dx ------- JV V<-O СР/
После интегрирования в пределах отсн дос0 и от т=0 до x=Tj получим
Час- <3-376>
Где tj—продолжительность первого периода сушки в час;
Си—начальное влагосодержание.
Скорость сушки при переменном влагосодержании сушильного агента. Как правило, в процессе сушки влагосодержание воздуха изменяется; оно непрерывно увеличивается при протекании воздуха вдоль сушилки и одновременном понижении его литературы.
Практически можно принять, что скорость сушки в этом случае пропорциональна разности хнас,.—х влагосодержаний воздуха, где хнас.—влагосодержание насыщенного воздуха, соответствующее температуре высушиваемого материала, в кгс/кгс сухого воздуха; х—влагосодержание воздуха в любой момент в кгс/кгс сухого воздуха.
Выделив элементарный участок непрерывно действующей сушилки, для которого Х—влагосодержание воздуха в кгс/кгс сухого воздуха, T—температура воздуха в °С, DF—поверхность материала в м2, можно считать, что на этом участке сушилки условия сушки являются постоянными и материал сушится с постоянной скоростью:
DW
-J^- == Кх (*нас. - *) (3—377)
Где Кх—коэффициент массопередачи, или коэффициент скорости сушки, в кгс/м2-час Ах.
Если через сушилку проходит L кгс/час абсолютно сухого воздуха, то за промежуток времени х им будет унесено влаги:
DW = Li Dx
Сопоставив последнее уравнение с уравнением (3—377), получим
|
С*нас. х) |
Dx
= KxdF (3—378)
Интегрируя последнее уравнение в пределах от хх—начального влагосодержания воздуха до л*2—его конечного влагосодержания и от 0 до Fx, Найдем общую поверхность, потребную для высушивания
Х2
1<~ X---- ZTT X------ =гт: (3-379)
J\x J Лнас. Л х^х лнас. Л1 *»
Уравнение (3—379) применимо лишь для первого периода сушки; когда же влагосодержание высушиваемого материала достигнет критической точки, активная поверхность сушки уменьшится до величины
F* = MF (3—380)
С
Причем принимают т= — (отношение свободного влагосодержания материала к кри - Со
Тическому).
Очевидно, уравнение (3—378) может быть применено и ко второму периоду сушки, если вместо величины F Подставить величину F'.
Подставив в уравнение (3—380) значение M И дифференцируя, получим
DF' = -F- DF со
При подстановке величины DF Вместо DF В уравнение (3—378 оно примет такой вид:
L Х DX X ~Kx~RdF (3-381)
Рассмотрим процесс сушки в противоточной сушилке. Обозначим:
Хх—влагосодержание входящего воздуха в кгс/кгс сухого воздуха; Х2—влагосодержание уходящего воздуха в кгс/кгс сухого воздуха; G—количество сухого материала, проходящего через сушилку, в кгс/час; L—количество сухого воздуха, проходящего через сушилку, в кгс/кгс, Сх—содержание свободной влаги в высушиваемом материале при входе в сушилку в
Кгс/кгс сухого вещества; F С—содержание свободной влаги в высушиваемом материале в любом сечении сушилки в кгс/кгс сухого вещества.
Материальный баланс влаги в любом сечении сушилки можно выразить следующим образом:
G (сх — с) = L {х2 — х)
Откуда
С — сх Q (х2 — х)
Подставляем найденное значение с в уравнение (3—381):
Интегрируя последнее уравнение, получим
Л*2
|
_ кх с Lc0 J |
|
DF |
|
(З—382> |
|
-*)J |
|
С^нас. — х) |
Dx
Сл — Q (х2
XI
|
|
Левую часть уравнения можно интегрировать аналитическим путем, так как переменным является только х. Действительно
Dx С
Dx
|
|
|
С^нас. х) |
|
|
Dx
■ CjG
Х "Т" £ --- Х2
( <Ф
|
Лучим |
Обозначив двучлен
Х2 J Через B И д-нас. через а и переставив пределы, по -
XI
Г_____ Dx________ Кх_ Г
|
(.X АГнас.) |
J (х-а){х+Ь) J DF
Х2
Левую часть этого уравнения можно проинтегрировать:
|
I |
|
1 |
|
Х + Ь |
Х\
Dx
In
(х — а) (х + Ь) а-\- Ъ
|
|
Тогда
G 1 L а + Ь
Хг + B 111 х2 + B (хг — а) (х2 + Ъ)
К,
In
А + B (х2 — а) (% + B) с0
Подставив действительные значения а и B И производя соответствующие преобразования, получим
CxG
|
G |
(■'"нас. х\) — In
Кл
CiG
• £ х2 С*"нас. xz) ixl 4" l х%
Обозначив
CxG
Получим уравнение второго периода сушки при переменных условиях в окончательном виде
|
(3 -383) |
G. С^нас. — А______________ Кх с
-f- А — х2 (-^нас. — XZ) (хх + ^ — х%)
Где F2—поверхность сушки, потребная для проведения второго периода сушки.
Уравнения (3—379) и (3—383), решенные относительно Fx И F2, Определяют необходимые размеры сушилки для получения открытой поверхности высушиваемого материала, равной Fx м7, в первом периоде и F2 Во втором периоде сушки.
Числовое значение коэффициента Кх Должно быть определено экспериментально путем опытной сушки при тех же самых условиях, которые прдеполагаются в заводских установках.
|
Х2 |
|
_ Кх F |
|
Х% |
|
In |
|
Ln |
|
Lc0 |
Приведенные методы расчета процесса сушки в постоянных и особенно в переменных условиях, несмотря на их сложность, дают приближенные результаты, и для их применения требуются соответствующие опытные данные.