АППАРАТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ
Фазовое равновесие жидких смесей
Классификация двухкомпонентных смесей. Если, вследствие теплового движения молекул, из жидкости в паровое пространство в единицу времени переходит столько же молекул, сколько перемещается обратно из пара в жидкость, то между жидкой смесью, заключенной в замкнутом сосуде, и паром над ней устанавливается подвижное фазовое „. равновесие.
Тепловое движение молекул является причиной расширения газа, которое обнаруживается как «термическое давление». Оно тем больше, чем выше температура и чем больше молекул в единице объема. Для идеальных газов термическое давление прямо пропорционально. абсолютной температуре и обратно пропорционально удельному объему. Термическое давление жидкости, обладающей, как известно, значительно меньшим удельным объемом, чем газ, при определенной температуре достигает нескольких тысяч атмосфер, т. е. значительно больше, чем газа. В идеальных газах, и^праКтическИ в парах, термическое давление уравновешивается внешним давлением; в жидкостях оно в значительной мере компенсируется направленным в противоположную сторону к о г е з и - онным давлением, которое обусловливается внутренними силами притяжения молекул. Избыток термического давления над когезион - і ным — это давление пара.
Парциальные давления газообразной или жидкой смеси следует также рассматривать как термическое давление отдельных компонентов, уменьшенное на величину когезионных сил. В смесях идеальных газов и паров, в которых когезионные силы ничтожно малы, парциальное давление каждого компонента равно термическому давлению и, следовательно, при данной температуре пропорционально числу молекул соответствующего компонента в единице объема.
Так как парциальные давления компонентов в смеси жидкостей определяются в основном когезионными силами, то необходимо прежде - всего рассмотреть взаимодействие отдельных молекул.
Пусть сила, с которой притягиваются в жидкости две соседние молекулы одного компонента, будет ап, сила взаимного притяжения двух молекул второго компонента а22 и, наконец, а12—сила притяжения молекул двух неодинаковых компонентов.
Если силы аи, а22 и а12 равны между собой, то жидкости взаимно растворимы друг в друге в любых отношениях и их смеси называются и д е а л ь. н ы. м и,, р а с т в о р а м и.
Общая сила, с которой какая-либо молекула удерживается в смеси, не зависит в этом случае от состава смеси, так как безразлично, окружена ли молекула большим количеством молекул первого или второго компонента. Парциальное давление компонента зависит лишь от числа его молекул, достигающих в единицу времени поверхности жидкости с минимальной скоростью, необходимой для преодоления когезионных сил. При данной температуре давление соответствующего компонента возрастает пропорционально его содержанию в жидкости.
В идеальных растворах равновесие между жидкостью и паром устанавливается по закону Рауля.
Если сила притяжения молекул двух неодинаковых компонентов ап будет меньше сил а1х и а22, то молекулы удерживаются в растворе слабее, чем в том случае, когда их окружают молекулы только одного компонента. Поэтому молекулы легче переходят в паровое пространство, и парциальное давление в таком растворе выше, чем в идеальном растворе (смеси с положительным отклонением от закона Рауля).
Имеются также смеси, в которых сила а12 значительно больше сил ап и а22. Тогда молекулы сильнее удерживаются в чистых компонентах, и поэтому парциальные давления меньше, чем в идеальных растворах (смеси с отрицательным отклонением от закона Рауля).
Если сила а12 очень мала по сравнению с а1Х и а22, то одинаковые молекулы стремятся соединиться, а разные молекулы отделяются друг от друга. В этом случае смеси расслаиваются и, следовательно, состоят из взаимно нерастворимых жидкостей.
Кроме идеальных растворов и смесей взаимно нерастворимых жидкостей, имеются смеси жидкостей, обладающих частичной растворимостью друг в друге.
Таким образом, все жидкие двухкомпонентные смеси, в зависимости от степени взаимной растворимости их компонентов, можно разделить на три группы:
жидкости, взаимно растворимые в любых отношениях;
жидкости, частично растворимые друг в друге;
жидкости, взаимно нерастворимые.
Жидкости, взаимно растворимые в любых отношениях. Когда жидкая смесь состоит из двух компонентов, полностью растворимых друг в друге, то упругость паров каждого компонента понижается и общее давление паров смеси, температура кипения и концентрация пара не являются постоянными, изменяясь в зависимости от изменения состава жидкой смеси.
Жидкости, взаимно растворимые в любых отношениях, делятся на три группы:
1. Смеси жидкостей, растворимых в любых отношениях, не обладающие постоянной температурой кипения. Выделяющийся при испарении таких жидкостей пар по своему составу отличается от состава жидкой смеси, причем легколетучего компонента в парах над жидкостью всегда больше, чем в жидкости. Температура кипения этих смесей в зависимости от их состава изменяется в пределах от температуры кипения одного чистого компонента до температуры кипения другого компонента.
Смесь двух жидкостей, взаимно растворимых в любых отношениях, представляет собой систему, состоящую из двух фаз и двух компонентов, и, следовательно, по правилу фаз является системой, имеющей две степени свободы.
Однако для практических целей одну переменную считают постоянной и строят диаграмму фаз в плоской системе координат. При этом можно получить следующие фазовые диаграммы: давление—температура (состав постоянный), давление—состав (температура постоянная), температура—состав (давление постоянное).
В качестве примера рассмотрим фазовые диаграммы для двух - компонентной смеси бензол—толуол.
Эта смесь является идеальной, и поэтому парциальные давления компонентов по закону Рауля (при постоянной температуре) равны: легколетучего компонента А (бензола)
Ра=раха
Труднолетучего компонента В (толуола)
Рв = РвО — *а)
Где Рд—упругость пара чистого компонента А; Рв—упругость пара чистого компонента В; Ха—молекулярная доля компонента А в жидкости; 1 — ха —молекулярная доля компонента В в жидкости.
Зная величины рА и pBj находим обшее давление Р паров смеси как сумму парциальных давлений компонентов
Р = РА + Рв = РАхА + Ръ( 1-ХА)
Из приведенных трех уравнений видно, что при постоянной температуре парциальные давления компонентов, а также общее давление паров смеси находятся в линейной зависимости от молекулярной доли хА легколетучего компонента в жидкости. На рис. 376, / эти зависимости представлены графически, причем прямые ОВ и DA изображают изменение парциальных давлений компонентов, а прямая АВ—изменение обшего давления.
Чтобы определить температуру кипения смеси заданного состава, строят указанным выше способом ряд изотерм АВ, А'В', А"В", выражающих общее давление паров при различных температурах (/, Ґ, і"). Линии парциальных давлений рА и рв получают соединением точек А, А', А" с точкой D и точек В, В', В" с точкой О.
Далее проводят горизонтальную прямую MN соответственно внешнему давлению. Восстановив из точки, соответствующей данному составу хА* вертикальную линию до пересечения с линией MN, находят точку R на изотерме T. При этой температуре T общее давление пара смеси равно внешнему давлению, и температура T будет температурой кипения смеси состава хА-
Если определить таким образом температуру кипения смесей разного состава (при одном и том же давлении), то, отложив по оси абсцисс составы, а по оси ординат соответствующие температуры кипения, получают кривую кипения, приведенную на рис. 376, II, для смеси бензол—толуол. Верхняя кривая на рисунке показывает равновесный состав пара при температуре кипения смеси.
При составе смеси хх долей моля легколетучего (бензола) и температуре tx практически имеется только одна жидкая фаза—смесь бензола и толуола. С повышением температуры смеси до t2 появится паровая фаза состава х2. Так как давление постоянно, то при наличии двух фаз будет только одна степень свободы и, следовательно, с изменением температуры изменится и состав фаз.
При дальнейшем повышении температуры количество жидкой фазы станет уменьшаться, а паровой увеличиваться, и при температуре когда состав пара окажется равным составу первоначальной смеси,
|
|
На этой же диаграмме можно изобразить процесс последовательной конденсации, исходя из паровой фазы состава х2, и путем ряда последовательных процессов конденсации и испарения получить жидкость, состоящую из одного чистого труднолетучего компонента.
Взаимное положение кривых в фазовых диаграммах определяется первым законом Д. П. Коновалова: пар обогащается тем компонентом, прибавление которого к жидкости повышает давление пара над ней или понижает ее температуру кипения. Этот закон применим к любым жидким смесям. Прибавление бензола к смеси бензол—толуол понижает температуру ее кипения, и поэтому концентрация бензола в паре будет выше, чем в жидкости. Из рис. 376 видно, что это отвечает такому расположению кривых, при котором кривая состава пара всегда выше кривой состава жидкости.
Приведенная на рис. 376, III диаграмма равновесия у—Х построена следующим образом. По оси ординат отложено содержание одного компонента в долях моля в паровой фазе (у), а по оси абсцисс—содержание того же компонента в жидкой фазе (х). Диаграмму обычно строят для постоянного общего давления и, реже, для / постоянной температурьіі
На рис. 376, III показана у—х-диаграмма дйя двухкомпонентной смеси бензол—толуол, причем по оси ординат отложено молярное содержание легколетучего компонента (бензола) в парах, а по оси абсцисс— молярное содержание того же легколетучего в жидкости в состоянии равновесия.
Диагональ соответствует равному содержанию легколетучего компонента в паре и жидкости х=у.
Кривая равновесия для растворов, подчиняющихся закону Рауля, может быть построена (см. стр. 457) по уравнению
УА =_____________ (3-165)
УА 1 + («-1)*А
Где а— —относительная летучесть. Чем больше числовое значение а,
Тем сильнее отклоняется кривая от диагонали, тем больше различие в составе пара и жидкости и тем легче разделить смесь на компоненты. На диаграмме у—х фазовые точки пара и жидкости сливаются в одну точку, всегда лежащую на кривой равновесия.
Кривая равновесия и диагональ ограничивают область взаимного существования двух фаз. Выше кривой равновесия расположена область пара, а ниже—область жидкости.
2. Смеси жидкостей, растворимых в любых отношениях, обладающие при некотором определенном составе постоянной температурой кипения. Эта температура больше температуры кипения чистых компонентов, составляющих смесь (смеси, обладающие максимальной температурой кипения); при этой температуре содержание компонентов в парах такое же, как и в жидкости.
Типичными примерами таких смесей являются водные растворы минеральных кислот, например водные растворы азотной и соляной кислот.
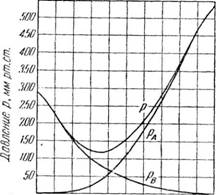
Фазовые диаграммы для смеси азотная кислота—вода представлены на рис. 377.
Чистая вода кипит при 100°, чистая азотная кислота—при 86°, раствор же HN03 в воде при содержании HN03 68,5% вес. кипит при постоянной температуре 121,9°.
На t—х-диаграмме (рис. 377, II) кривая зависимости температуры кипения такой смеси от ее состава имеет максимум температуры кипения (точка М). В согласии с законом Коновалова верхняя кривая отвечает составу пара, нижняя—составу жидкости при разных температурах кипения и постоянном давлении.
На рис. 377, III изображена у—х-диаграмма для смеси азотная кислота—вода. Точка М, в которой кривая пересекает диагональ, соответ-
|
0 10 20 30 40 50 60 70 80 00 100 |
|
Содержание легколе/пуоегп (азотной кисло/77ь/), %мол I |
550
80 О
/О 20 30 40 50 60 70 80 SO 77777 Содержал/іє леллол/е/пу/его /азотной и и ело П7ь/), %тл II
Рис. 377. Диаграммы р—х (1), І—х (11) и у—Х (111) для смеси с максимальной температурой кипения (азотная кислота—вода).
Ствует одинаковому составу жидкости и пара; ее называют характеристической точкой. Наличие такой точки указывает на то, что смесь невозможно разделить на составляющие ее чистые компоненты.
3. Смеси жидкостей, взаимно рас - ЮО творимых в любых отношениях, обладающие при некотором определенном составе постоянной температурой кипения, меньшей температуры кипения чистых компонентов, составляющих смесь (смеси, обладающие минимальной температурой кипения). При перегонке таких жидкостей с некоторой постоянной температурой кипения состав пара будет одинаков с составом жидкости и: следовательно, их также невозможно разделить на чистые компоненты.
Типичными примерами таких смесей являются смеси этилового спирта с водой и этилового спирта с бензолом.
С одинаковым составом жидкости и пара.
Смеси, обладающие максимумом или минимумом температуры кипения, при перегонке можно разделить на нераздельнокипящую смесь состава х0 в отгоне и избыточный (сравнительно с составом нераздельно - кипящей смеси) компонент в остатке; получить оба компонента в чистом виде путем перегонки таких смесей невозможно.
В качестве примера рассмотрим фазовую диаграмму на рис. 377, II. Жидкость начального состава х>х0 кипит при температуре tx и дает пар состава у, обогащенный более летучим компонентом. В процессе перегонки жидкость будет обогащаться менее летучим компонентом и точка х перемещается влево. В результате можно получить чистый более летучий компонент в дистилляте и нераздельнокипящую смесь состава х0 в остатке, но дальнейшее разделение смеси невозможно, так как она кипит без изменения состава
Если начальная смесь имеет состав х'<Сх0, то она закипает при температуре tx и дает пар состава у', обогащенный менее летучим компонентом. В процессе перегонки точка х' перемещается вправо, и перегонка приводит к разделению смеси на менее летучий компонент в дистилляте и нераздельнокипящую смесь в остатке.
Жидкости, частично растворимые друг в друге. Исследования смесей частично растворимых друг в друге жидкостей были впервые проведены Абашевым и Алексеевым[4]. Алексеев показал возможность построения характерных параболических кривых растворимости. Каждая из кривых состоит из двух ветвей, сходящихся вместе в температурной точке "наибольшей растворимости. До этой точки обе жидкости при смешений дают в известных пределах концентраций два слоя, представляющие собой два раствора различного состава (раствор жидкости А в) жидкости В и раствор жидкости В в жидкости А). В общей точке оба раствора обладают одинаковым составом.
Температура, соответствующая этой максимальной точке, называется критической температурой растворения. При более высокой температуре обе жидкости смешиваются, т. е. взаимно растворяются в любых отношениях.
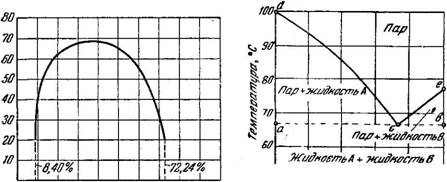
Классическим примером частично растворимых жидкостей являются фенол и вода. При 20° вода растворяет 8,4% фенола, а при 50° растворимость фенола в воде увеличивается до 12,08%. Фенол в свою очередь растворяет воду при 20° в количестве 27,76% и при 50°—37,17%.
Если взаимную растворимость фенола и воды изобразить на диаграмме (рис. 379), то оказывается, что кривые растворимости представляют одну кривую, проходящую через максимум в точке, соответствующей составу 35,99% фенола при £=68,8°.
Если при температуре 20° к воде прибавлять фенол, то он будет переходить в раствор до тех пор, пока не получится раствор, содержащий —8,4% фенола. При дальнейшем прибавлении фенола возникает второй слой фенола, в котором будет растворено 27,76% воды. Последующее прибавление фенола не оказывает какого-либо влияния на концентрацию фаз, изменяя лишь относительные количества их при постоянном процентном составе, до тех пор, пока не будет прибавлено такое количество фенола, что система будет содержать фенол и воду в отношении 72,24 к 27,76. После этого дальнейшее прибавление фенола вызовет исчезновение слоя воды с содержанием 8,4% фенола и система вновь будет состоять из двух фаз—жидкой и паровой.
Когда в системе имеется только одна жидкая и одна паровая фазы, то^к ней приложимо все, что было сказано о жидкостях, полностью рас
творимых одна в другой. При двух жидких фазах и одной паровой давление паров смеси остается постоянным до тех пор, пока сохраняются оба слоя, т. е. такая система является разновидностью смеси взаимно нерастворимых жидкостей.
Наблюдаются и такие случаи ограниченной растворимости двух жидкостей, когда полная взаимная растворимость наступает не при повышении, а при понижении температуры. Примером может служить смесь воды и триэтиламина, для которой существует минимальная критическая температура растворения, равная 20°.
|
Рис. 380. Диаграмма T—х для несме - шивающихся жидкостей. |
|
О 10 20 30 40 50 60 70 80 90 /00 Содержание еренош^ % |
|
Рис. 379. Диаграмма г взаимной растворимости фенола и воды. |
|
|
Некоторые смеси двух жидкостей (например, никотина и воды) имеют максимальную и минимальную критические температуры растворения и, следовательно, кривая их взаимной растворимости представляет замкнутую линию.
Жидкости, взаимно нерастворимые. Когда смешаны две взаимонерастворимые жидкости, то каждая из них полностью сохраняет свои свойства. Такая смесь легко может быть разделена на составные части механическим путем, при помощи отстаивания. Система состоит из двух компонентов и трех фаз и, следовательно, обладает одной степенью свободы. Это - указывает на то, что каждой определенной температуре смеси будет соответствовать вполне определенное давление и каждый из компонентов будет вести себя так как будто он находится один в чистом виде.
Иными словами, в смеси, состоящей из взаимно нерастворимых жидкостей, парциальное давление каждого компонента не зависит от его содержания в смеси и равно давлению паров чистого компонента при той же температуре.
Диаграмма равновесия несмешивающихся жидкостей при постоянном давлении (Р=760 мм рт. ст.) изображена на рис. 380, где по оси ординат отложена температура, а по оси абсцисс—содержание компонентов А и В. В точке а существует только компонент А, а в точке Ь—только компонент В.
Горизонталь ab на диаграмме ограничивает область существования смеси жидкостей А и В, а точка с соответствует состоянию кипения смеси, причем температура кипения смеси лежит ниже температуры кипения отдельных компонентов. Это свойство используется в технике для
перегонки высококипящих жидкостей с паром. Соотношение между весовыми количествами компонентов в парах находят по формуле
СА РА МА
Абсолютно нерастворимых жидкостей в природе не существует; степень их растворимости в большой мере зависит от температуры. В некоторых случаях незначительной растворимостью пренебрегают, считая жидкости практически взаимно нерастворимыми, что дает возможность пользоваться приведенной формулой (3—166).