АППАРАТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ

Число тарелок тарельчатой колонны

Общие сведения. Для расчета числа тарелок тарельчатой абсорбци­онной колонны определяют графическим путем число ступеней изменения концентрации. Для этого на диаграмме Y—X в том или ином масштабе откладывают по оси абсцисс концентрации X абсорбируемого газа в кг-мол/кг-мол растворителя, а по оси ординат У—концентрации абсорби­руемого газа в газовой смеси в кг-мол/кг-мол инертного газа.

На диаграмму наносят кривую равновесия—в случае линейной равновесной зависимости, по уравнению^(3—70)

V =3—_

*р 1^(1—ЛОЛ.

Или по опытным данным в случае любой другой равновесной зависимости. На диаграмму наносят также линию рабочих концентраций по уравнению (3—77)

Ки-Ук = т(Хк-Ан)

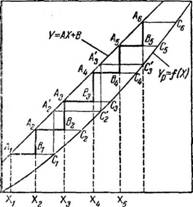
На линии рабочих концентраций находят точки А и Лк, соответствую­щие начальной и конечной концентрации жидкости. Проводя из точки А до точки Ак последовательно горизонтали и вертикали между линией рабочих концентраций и кривой равновесия, получают ломаную, число ступеней которой будет показывать число ступеней изменения концентра­ций при заданных условиях работы абсорбционной колонны.

Вводя понятие ступени измЕнения концентрациИ (см. стр. 471), мы делаем следующее допущение:" в результате взаимодействия фаз в каждом элементе колонны, соответствующем одной ступени изменения кон­
центрации, имеет место Фазовое равновесие, при котором состав жидкости Хп на выходе ее из данного элемента п равен равновесному составу жидко­сти Хп-1 при входе ее в этот элемент (при отсчете числа ступеней сверху вниз). На диаграмме ступени изменения концентрации изображены лини­ями АхСхХ2, А2С2А3, АзСзА6 (рис. 351).

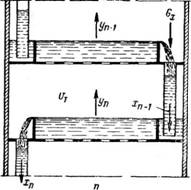
Рис. 351. Схема массообмена на тарелке.

Теоретически можно предположить, что в пределе каждая тарелка колонны соответствует одной ступени изменения концентрации. Однако стекающая с тарелки колонны жидкость никогда практически не дости­гает равновесного состава при входе жидкости на тарелку, т. е. прак­тически всегда Х„<Х(П_1)р. Поэтому число тарелок А/т, необходимое для поглощения газа при заданных условиях, всегда значительно больше числа ступеней изменения концентрации Nc, необходимых при тех же ус­ловиях, т. е. всегда NT>NC. В действительНости изменение состава фаз на тарелке изображается на диагр*амме"ломаной АХВхА2.

Методы определения числа тарелок NT по числу ступеней изменения концентрации Nc для заданных условий абсорбции (так же, как и для дру­гих диффузионных процессов) не разработаны. Обычно число тарелок на­ходят путем деления найденного графическим путем числа ступеней изме­нения концентрации на так называемый к. п. д. тарелки:

(3—117)

Где rlT—коэффициент полезного действия тарелки имеет такой Гвид:

Хп — - Х/г-і

(3-118)

(п-1)р

И числовые значения его принимаются практически в пределах от 0,2 до 0,8.

Числитель (Хп—Хп_і) дроби, выражающей к. п. д. тарелки,—это из­менение рабочей концентрации жидкости на данной тарелке, а знамена­тель (Х(/г_1)р—Xn_i)—движущая сила процесса при входе жидкости на эту тарелку. Следовательно, отношение

Хп — Xn-I

1(п - 1)р

Представляет собой по физическому смыслу действительное число единиц переноса на данной ступени фазового контакта или тарелки, которое обозначаем как тут.

Отношение числа единиц переноса одной ступени тус к действительному числу единиц переноса на данной тарелке туТ

(3—119)

Представляет собой число тарелок, соответствующее или эквивалентное одной ступени изменения кон­центрации.

В случае линейной равновесной зависимости число единиц переноса для всех ступеней изменения концентрации в заданных условиях проведе­ния процесса является величиной постоянной и, следовательно, постоян­ной величиной можно в этом случае считать и Ет.

Если равновесная зависимость не линейна, то число единиц пере­носа для отдельных ступеней изменения концентрации не одинаково и, следовательно, число тарелок, эквивалентное одной ступени изменения концентрации, является величиной переменной. Поэтому для определения числа тарелок тарельчатых колонн приходится принимать среднее зна­чение этого числа Еср., общее для всех тарелок, определяя N.Г как

NT = Ecp.Nc

Величина ЕсР. характеризует несовершенство массообмена на та­релках, и чем менее совершенно работает тарелка, тем больше эта вели­чина. Число тарелок, эквивалентное одной ступени изменения концентра­ции, зависит от физических свойств участвующих в массообмене жидкостей и газов, от гидродинамических условий взаимодействия фаз (характеризуе­мых скоростью газа или пара в колонне, в отверстиях тарелок и прорезях колпачков на тарелках), от глубины погружения прорезей в жидкости, от расстояния между тарелками и других факторов. Числовое значение ЕсР. в значительной мере зависит от взаимного направления движения фаз в колонне и механического уноса капель жидкости газом или паром. Поэтому достаточно точно число тарелок, эквивалентное одной ступени изменения концентрации, может быть определено только опытным путем. Практически £ср. равно от 1,25 до 5; для большинства случаев можно принять 1,5—2.

Графический метод определения числа тарелок на основе общих положений массопередачи. Изложенный выше графический метод опре­деления числа тарелок тарельчатых диффузионных аппаратов имеет существенный недостаток. Для перехода от числа_ сТупеней изменения Концентрации к числу тарелок необходимо знатьГлибо числовое значение к. п. д. тАрелки, либо Число тарелок, эквивалентное одной ступени изме - 'нения концентрации, однако и то и другое обычно неизвестно. Кроме того, не учитываются кинетичЕские зависимости, описываемые общими Уравнениями массопередачИ,

В связи с этим нами предложен графический метод определения числа тарелок на основе общих уравнений массопередачи, одинаково пригодный для любого диффузионного процесса[2]. Этот метод заключается в следую­щем.

Примем в качестве основной характеристики участвующих в массо - обмене фаз концентрацию (X) распределяемого между фазами вещества в жидкой фазе. Схема массообмена на тарелке в процессе абсорбции при - ^ нимается такой: жидкость на вышележащей тарелке (п—1) имеет концен­трацию, равную X„_i. Эта жидкость по сливному патрубку стекает на нижерасположенную тарелку п, где вследствие массообмена между фазами ее концентрация изменяется от Хп_і до Хп.

Если расход жидкости в аппарате равен Gx, то для рассматриваемой тарелки п (см. рис. 351) количество вещества, переходящего из одной фа­зы в другую, определяется равенством

G={Gx(Xn_ I-Xn) (а)

Это же количество распределяемого между фазами вещества опреде­ляется из основного уравнения массопередачи

G = KxFLXn

Или, принимая '--------------

F = AVT

. получим

G = KxaV,AXn

Или

G = KXvVT АХп (б)

Где Vr—объем жидкости на тарелке в Ms\ F—поверхность фазового контакта в м2; а—удельная поверхность фазового контакта в м21м3ш, г ДХП—средняя движущая сила процесса в долях моля;

Кxv—коэффициент массопередачи в кг-мол! мь-час.

Из сопоставления равенств (а) и (б) находим:

Хп~і Хп _____ Kxv^r / \

Ш~п (в>

Для определения движущей силы процесса примем следующие до­пущения:

1) в пределах одной тарелки концентрация жидкости изменяется прямолинейно;

2) при расчете движущей силы концентрация распределяемого между фазами вещества в газовой фазе над жидкостью (на тарелке) принимается постоянной и равной среднему значению ее на выходе с тарелки. По этой концентрации и определяется равновесная концентрация, т. е. по ве­личине У(п—и , используя кривую равновесия (см. рис. 351), находим кон-

: центрацию жидкости Х(п-i)p, от которой и отсчитываем движущую силу ДХщ и ДХп2.

При этих допущениях среднюю движущую силу процесса на тарелке можно вычислить как среднюю логарифмическую между значениями на входе

= X (п_1)р — Х„_ і

И на выходе

По общему уравнению

Д^ ____ 1^(/г-1)р —Хп\ — [Х(п_1)р — Aff-IJ

In Х("-1)Р ~ Хп

Х(П— 1)р —

ДХ = ----------------------------------------------------- Хп-1 — Хп____ /гч

V _ X у '

In Л("-')Р Лп

Х(п— 1)р ~Хп-1

Подставляя значение АХ„ из равенства (г) в равенство (в), получим.

Х„_, - X : ~ ХГ"Хах =1" ^^^ = Кг~ (А)

Ч

По физическому смыслу левая часть равенства (д) представляет собой число единиц переноса для одной тарелки тх т и, таким образом, для та­рельчатых аппаратов

M,VT = In(е)

(П—1)р И—1

Тхт = Кфі (3-120)

Emxt = CV (3—121)

= Emy?=Cv (3—121а)

В случае4 если тарелка по своим конструктивным особенностям и условиям проведения процесса рассматривается как аппарат полного смешения, кинетические соотношения можно установить из уравнения

DX , у - V \ Gx —Л„_, )

И уравнение массопередачи можно написать в таком виде:

= (Х(п_1)р — X«-I) КХ1, Сопоставление последних двух уравнений дает

Уравнения (3—120), (3—120а), (3—121) и (3—121а) дают возможность графически определить непосредственно число тарелок тарельчатых ап­паратов и основные размеры тарелок. По уравнениям (3—120) и (3—121) можно на диаграмме У—X графически получить связь концентраций распределяемого между фазами вещества в жидкости на входе на тарелку и на выходе с нее со средней концентрацией того же вещества в газе на выходе с тарелки. При применении уравнений (3—120а) и (3—121а) гра­фические построения выражают зависимость между концентрацией в газе на входе на тарелку и на выходе с тарелки и средней концентрацией жидкости на выходе с тарелки.

Допустим, что для определения числа тарелок будем исходить из уравнения (3—120). Нанесем на диаграмму У—X в определенном масшта­бе кривую равновесия и линию рабочих концентраций (см. рис. 351). Предварительно вычислим значения величин Kxv> Gx, начальная и ко­нечная концентрации Хн и Хк распределяемого между фазами вещества в жидкости заданы.

Ведем отсчет тарелок сверху вниз, т. е. принимаем за первую тарелку верхнюю, на которой концентрация жидкости Хн=Хх. На диаграмме рабочей концентрации Хх будет соответствовать точка Ах, а равновесной ей концентрации Х1р—точка Сх. По уравнению (3—120) находим числовое значение тх-т по уравнению (3—121)

Х]Р — ____ ртХТ__ г __

Х1р-Х2——^ BjCi

По полученному отношению —-1- находим на диаграмме точку Вх, абс-

ВІсі

Цисса которой будет соответствовать концентрации жидкости Х2 на вто­рой тарелке. Этой концентрации на линии рабэчих концентраций соответ­ствует точка А2 и на кривой равновесия точка С2, соответствующая кон - . х центрации Х2р.

По отношению -=СХ находим точку В2, абсцисса которой будет

ДА

Соответствовать рабочей концентрации на третьей тарелке Х3. Этой кон­центрации на линии рабочих концентраций будет соответствовать точка А з и равновесной ей концентрации Хзр на кривой равновесия—точка С5 и так далее до тех пор, пока не будет получена точка Асоответствую­щая заданной конечной концентрации жидкости Хп=Хк. Число полученных і на диаграмме ступеней или горизонтальных отрезков АВ будет числом тарелок Nr.

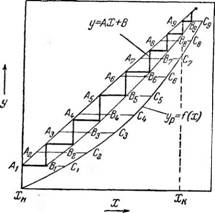
Практически построение ломаной линии для определения числа та­релок можно упростить. При заданных условиях работы колонны вели­чина Сх является постоянной. Зная числовое значение Сх, можно на диаграм­му предварительно нанести кривую, представляющую собой геометриче­ское место точек Вх, В2 и т. д. Для этого (рис. 352) из произвольно взятых точек на линии рабочих концентраций проводим между линией рабочих концентраций и кривой равновесия горизонтали АХСХ, А2С2 и т. д. и,

АС

Разделив их в отношении Сх=-=^, проводим через найденные точки Вх,

ВС

В2 и др. вспомогательную кривую. Проводя, начиная от точки Ах (лежащей на линии рабочих концентраций и соответствующей начальной концентрации жидкости) последовательно горизонтали и вертикали между линией ра­бочих концентраций и вспомогательной кривой, в пределах от заданной концентрации жидкости Хн до заданной конечной концентрации жидкости Хк, получим ломаную линию. Число ступеней ломаной линии, или число горизонтальных отрезков, будет числом тарелок колонны Nr.

Аналогичным образом можно определить число реальных тарелок и по уравнению (3—121а), с тем лишь отличием, что отрезки АС на диаграм­ме будут вертикальными и точки В будем находить из отношения

Q __ Уп Y П р

У Уп-1 — Yп р

Объем жидкости на тарелке VT в уравнениях (3—120) и (3—120а) определяется из выражения

L/T = 0,001/zTJFCB. м* (3—123)

Где /?т—высота слоя жидкости на тарелке в мм\

FCB—площадь свободного сечения колонного тарельчатого аппа­рата в м2.

Высота слоя жидкости на тарелке практически изменяется в незна­чительных пределах и составляет /гт—40 ч-60 мм.

Площадь свободного сечения тарельчатого аппарата определяется из равенства

FCB.=FK(\-*) М* (3-124)

Где FK—общая площадь сечения ап­парата в м2\ 9—доля общего сечения аппа­рата, занятая паровыми пат­рубками, колпачками и пе­реливными трубками. Минимальное расстояние меж­ду тарелками определяется из урав­нения

= + (3-125)

Где Ьр—перепад давления на тарелке в кгс/см2;

Ус—удельный вес жидкости в сливном патрубке, кгс/м3;

Hd—скоростной напор в сливном патрубке в м.

Площадь общего сечения аппарата FK определяется в зависимости от заданного количества пара, протекающего по аппарату, и принятой скорости пара в аппарате.

В расчетах тарельчатых аппаратов по изложенной схеме непосред­ственно не учитывается механический унос жидкости поднимающимися с тарелки парами или газами. Несомненно, практически унос жидкости с нижележащих тарелок на лежащие выше приводит к некоторому смещению концентрации по высоте аппарата и уменьшению движущей силы процесса. Это смещение будет тем большим, чем с большей скоростью протекают пары через жидкость на терелке и чем меньше расстояние меж­ду тарелками. Некоторые авторы рекомендуют учитывать этот фактор путем введения в расчетные формулы для определения числа тарелок по­правочного коэффициента ф. Однако в этом возможно и нет необходимости, так как фактор уноса жидкости парами и газами с тарелки на тарелку мо­жет быть учтен коэффициентами массопередачи Кх1, или Kyv, числовые значения которых определяются экспериментально в зависимости от ско-
рости протекания газа или пара в аппарате и других условий работы диф­фузионного аппарата данного типа.

Определение числа тарелок по поверхности фазового контакта. Если имеется возможность найти числовые значения коэффициентов массопередачи, то число тарелок можно определить аналитическим путем, по общим уравнениям массопередачи. В этом случае из уравне­ний массопередачи находят поверхность фазового контакта, необходи­мую для осуществления процесса в заданных условиях по одному из урав­нений:

F = Д.»

ІУ — Ур

F— DX М2

K.X J Xv — X

В барботажных аппаратах поверхностью фазового контакта яв­ляется общая боковая поверхность газовых (паровых) пузырьков, прохо­дящих через жидкость на тарелках:

F = ZT:Dn М2

Где z—число газовых или паровых пузырьков, проходящих через ко­лонну в час; dn—диаметр пузырьков в м.

Если

V,—объем газа или пара, проходящего через колонну, в мъ1час\ hT—высота слоя жидкости на тарелке в м; ш0—скорость подъема пузырьков в жидкой среде в м/сек; х NT—число тарелок в колонне, * то

__ VyhTHT

-g - о>о-3600

Подставив найденное число пузырьков в предыдущее уравнение

И решая его относительно числа тарелок jVT, получим:

N ™(3_126)

VYtli

Если газовые (паровые) пузырьки образуются при прохождении газа (пара) через прорези в колпачках в колоннах с колпачковыми тарел - . ками, то диаметр пузырьков определяется из равенства:

^(Т,-ТУ) = 2 (/ + 6) о,

Как

Dn= 1,56іУШЕЖЇ (3-127))

V Ух-уу

Где I—высота прорезей в м\ b—ширина прорезей в м; . ах—поверхностное натяжение в кгс/м.

В колоннах с ситчатыми тарелками

Тid®

-Q- (іх—1у)='КСІо0л

Откуда

Dn= 1,82 j/—^— (3-127а)

Где D0—диаметр отверстий в тарелке, через которые проходит газ или пар, в м.

Скорость подъема пузырьков в жидкой среде определяется так же,

Как скорость осаждения мелких взвешенных частиц по формуле

М/Сек

0 duyx

И зависит от режима движения пузырьков. По предыдущему

W = Аг

Где критерий Архимеда в данном случае:

4ёР2х (Ух - Ту)

Аг

\3Ьх

По опытным данным[3], если Re<$ или Лг< 162, то

24

И, следовательно

Я* — .

18

Если Re>9 и Агу 162, то

Re=\A\VAr (3—128а)