АППАРАТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ
Уравнения массопередачи
Основные уравнения массопередачи. Практически при проведении диффузионных процессов в аппаратах непрерывного действия, работающих по принципу противотока, процесс массообмена является установившимся и, следовательно, состав фаз в этих случаях изменяется только по поверхности фазового, кон - такта, оставаясь постоянным во времени для любого сечения аппарата, у
В двухфазной системе, состоя - р'к' щей из фаз Фх и Фу, как это было показано выше, возможно протека - Ун ние процесса массопередачи в двух направлениях: в одном случае рас - х пределяемый между фазами компо - " нент переходит из фазы Фу в фазу Фг., в другом, наоборот, переходит из фазы Фх в фазу Фу, причем в обоих случаях движущая сила процесса может быть выражена либо через концентрацию распределяемого между фазами компонента в фазе
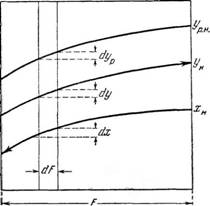
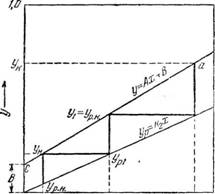
Фу, л - 'о через концентрацию этого же компонента в фазе Ф^. Выразив движущую силу процесса через концентрацию в фазе Фу, рассмотрим случай массопередачи, когда распределяемый между фазами компонент переходит из фазы Ф^ в фазу Фу (рис. 315). Примем обозначения: Gv—количество фазы Фу в кг-мол/час, Gx—количество фазы Фх в кг-мол/час\ G—количество распределяемого между фазами компонента, переходящего за время т из фазы Фх в фазу Фу, в кг-мол•
|
Рис. 315. К выводу основного уравнения массопередачи (при переходе распределяемого между фазами вещества из фазы в фазу Фу и выражении движущей силы процесса в концентрациях фазы Фу). |
30 А г. Касаткин.
Хи и хк—начальное и конечное содержание распределяемого между фазами компонента в фазе Фх в долях моля;
Уп и У к—начальное и конечное содержание распределяемого между фазами компонента в фазе Фу в долях моля;
Ур. цКУр. к—начальное и конечное равновесное содержание распределяемого между фазами компонента в долях моля; у, хи ур, хр—содержание распределяемого между фазами компонента в фазе Фу, в фазе Ф^- и равновесное, в любом сечении аппарата в долях моля;
F—поверхность фазового контакта* в м2.
Выделим в аппарате бесконечно малый элемент поверхности dF. За промежуток времени т на этом элементе поверхности из фазы Фх в фазу Фу согласно уравнение (3—28) перейдет количество компонента, распределяемого между фазами:
DG = Кух (ур — У) DF кг-мол (3—30)
При этом содержание данного компонента изменится в фазе Ф на величину
, DG Dy==-G7X
И в фазе Фх на величину
6\.т
В случае линейной равновесной зависимости
*
LJp=kxX
И, следовательно
VG
Dyp = Kxdx =
А изменение движущеи силы процесса на выделенном элементе поверхности составит:
Откуда
DG — ~CJ)
П
K} 1
Gxi Gy т
Подставив найденное Значение dG в уравнение (3—30), получим
TOC \o "1-3" \h \z D (УР - У) //Р — у V
Или
(Fp Н-^к) F
С ^Р -_у)^пК с DF
Ут> — У у 1
(■"п. к-%) 0
Откуда
In Ь-"' ^ = пкхр (3—31)
Ур к ~ Уп У к
Имея в виду; что
Г/р. н— Ук=*У«
И
Ур. к — Уи =
Уравнение (3—31) можно переписать в таком виде:
In ^=nKyxF (3-32)
Уравнение материального баланса для данного случая, принимая Gy и Gx постоянными величинами, выражается для фазы Фу как
G = Gy (ук — ун) х
И для фазы Фх как
G = GX (хн — хк) т = Gx -J- (ур. н — ур. к) х
Подставив последние два уравнения в выражение для п, получим:
H _J_\_______ Ур- н — УР. К — Ук + Ун (Ур. п — Ук) — (ур. к — /Ун)
П 1 ^ G.,Z I G G
У ИЛИ
Ау"~л? ук (3—33)
Подставив найденное значение п в уравнение (3—32) и решая это уравнение относительно G, получим
П К с. АУн — АУк
Или
G = KyFxAycf>. /сгс (3-34)
Где
Так как в условиях противотока понятия «начальное» и «конечное» состояние относительно поверхности фазового контакта являются неопределенными, то для того, чтобы числитель и знаменатель дроби в уравнении (3—35) были положительными, в дальнейшем будем всегда за начальную разность концентраций принимать наибольшую, обозначая ее Дуг, и за конечную разность—наименьшую, обозначая ее Д*/2. Тогда уравнение (3—35) примет вид:
= (3-36)
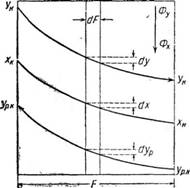
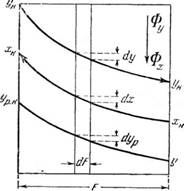
Выражая движущую силу процесса в концентрациях распределяе - "мого между фазами вещества в фазе Фх, .найдем аналогично для случая перехода данного компонента из фазы Фх в фазу (как это представлено на рис. 316):
G=KxFxAxcp. (3—37)
Где
Ахг — Алга
Ьх^^ТЇ (3-38)
2'31G Дх!
— хк
Дхк — хн Хрт к
И соответственно Axx наибольшая и Дл:2—наименьшая разности.
|
Р. н |
|
F- |
|
Т Р. н |
|
Рис. 316. К выводу основного уравнения массопередачи (при переходе распределяемого между фазами вещества из фазы в фазу Фу и при выражении движущей силы процесса в концентрациях фазы Фд-). |
Аналогичные уравнения могут быть поручены и для случая перехода распределяемого между фазами компонента из фазы Фу в фазу Фх при выражении движущей силы процесса через концентрации в фазе Фу. Для этого случая получим уравнения (3—34) и (3—35) и согласно рис. 317:
А У» = Unt- Ур. к '
&Ук=Ук — У р. и
|
Рис. 317. К выводу основного уравнения массопередачи (при переходе распределяемого между фазами вещества из фазы Фу в фазу Фу и при выражении движущей силы процесса в концентрациях фазы Фд,). |
|
Рис. 318. К выводу основного уравнения массопередачи (при переходе распределяемого между фазами вещества из фазы Фу в фазу Фу и при выражении движущей силы процесса в концентрациях фазы ФЛ). |
|
При этом |
А при выражении движущей силы через концентрации в фазе Фх получим уравнения (3—37) и (3—38) и согласно рис. 318:
&Xj= Хг
VP- Н
Дх„ =Fx
Р. к
Уравнения (3—34), (3—35), (3—37) и (3—38) являются основными уравнениями массопередачи. Через заданные величины начальных и конечных концентраций распределяемого между фазами компонента они связывают производительность диффузионных аппаратов и поверхность фазового контакта, необходимую для обеспе
чения заданной производительности. Эта поверхность определяется из вь: ражений
(3-39а)
Уравнения массопередачи для насадочных диффузионных аппаратов. Если диффузионный процесс проводится в колонне, заполненной насадочными телами, то высоту насадки обычно определяют по заданной производительности аппарата.
Обозначим: V—объем, заполненный насадкой, в м3\ Н—высота насадки в м\ f—площадь свободного сечения аппарата в м2\ а—удельная поверхность насадки в м2/м3. Тогда
F = aV м2 (3—40)
V = FH м3 (3—40а)
И, следовательно
F — AfH М2
Н = (3-41)
При линейной равновесной зависимости
Я = —пгА------------- м (3—42)
Н = f„-G.--------- м (3—42а)
Общее число единиц переноса. Подставив в уравнение (3—42) значение G из уравнений материального баланса
G = Gy (Уг — Уъ)* G = GX {хх — х2) т
Получим
|
У1 — У2 |
|
Н = Н = |
|
А]Ку Дг/ср. Gx XI — Х2 |
|
AfKx Дх, |
|
Ср. |
|
|
* или
H = Hymy М (3—43)
Н = Hxmx м (3—43а)
Где mv = у\~у* и mx— X1~X°-------- изменение рабочей кон -
У Д^ср. А Д*ср. ^
Центрации распределяемого между фазами компонента, приходящееся на одну единицу движущей силы; эту величину называют общим числом единиц переноса.
Величины
|
К- |
|
(3-44) (3—44а) |
|
М |
|
AfKy G |
|
М |
|
AfKx |
|
|
По смыслу уравнений (3—44) и (3—44а) приобретают значения высоты рабочей части или высоты насадки диффузионного аппарат а, соответствующей или эквивалентной одной единице переноса.
Для_:шобод__р^новесной зависимости общее число единиц переноса можно представить в более общем виде, исключив At/cp - и Ді'Ср. Для элемента фазового контакта dF по предыдущему имеет место равенство
|
|
|
КухІУг |
|
Y)DF |
DG = XG.,Dy
|
|
Откуда
DF =
—^ Г ~~ J
Ур — У
Подставив найденное значение F в уравнение (3—41), получим
|
И J Ур |
|
|
|
Н АГКу И соответственно С |
|
Или по предыдущему Н — hymy Н — hxmx |
|
Где |
|
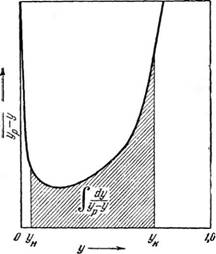
Рис. 319. Графическое определение обще^ го числа единиц переноса. |
|
Dx |
|
Н = |
|
AfKx |
|
_ Г Dy |
Gv С Dy
(3-46)
(3—46а)
(3-47) (3—47а)
|
Mv == \ У J Ур |
|
Dx |
|
Тг = |
(3-48) (3—-48а)
У
Новые выражения общего числа единиц переноса.
Интегралы в уравнениях (3—48) и (3—48а) решаются в заданных
Пределах графически. Для этого строят кривую в координатах * —у или
Ур У
-х и измеряют по масштабу площадь*(рис. 319), заключенную
1
Между кривой, осью абсцисс и ординатами, проведенными через заданные точки ук и г/к в первом случае и через точки хн и хн—во втором случае.
|
Dy |
|
Ky YP~Y Dy |
|
(3-45) |
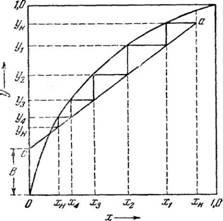
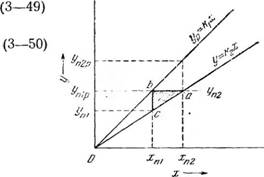
Ступени изменения концентрации. Примем, как это представлено на диаграмме - рис. 320, такой объем диффузионного аппарата, у кото
рого концентрация распределяемого между фазами компонента на выходе из него уп* равна равновесной концентрации на входе в него уРп1. Это изменение концентрации назовем ступенью изменения концентрации.
Очевидно, число единиц переноса, соответствующее одной ступени изменения концентрации, тус или тхс, найдем как
|
(3-51) |
|
(3—52) |
|
Рис. 320. Ступень изменения концентрации. |
|
&Х, |
|
Или в интегральной форме как |
|
= г J Ур- |
|
Т. |
|
(Х~Хр)п2 С Dx \ (X~XPhl |
|
(3—53) |
__ Уп2 --- Ут
Tyn ср. ХП\ Хп2
ТГг.=
При заданных величинах начальной и конечной концентрации распределяемого между фазами компонента число ступеней изменения концентрации Л/с в случае линейной равновесной зависимости может быть определено аналитически. Число ступеней вычисляется как частное от деления общего числа единиц переноса ту: определяемого при заданных рабочих концентрациях по уравнению (3—48), на число единиц переноса одной ступени rnvc, принимаемого по уравнениям~[3::-:5Э) и (З^-ЗЗІ):
[NC = ^L ]
|
(3—54) |
|
Где к |
IЕ Мус (
Для перехода от числа ступеней к высоте насадки насадочных колонн можно написать уравнение
Н = HvcNc
Ус—высота насадки, эквивалентная одной ступени изменения концентрации.
Из сравнения уравнений (3—47), (3—53), (3—54) видно, что
|
|
|
У с An |
|
Ус |
Н = Hymy ■■
|
|
|
Откуда |
|
(3—55) |
Hyc = Hymyc
|
|
Т. е. высота hyc, эквивалентная одной ступени изменения концентрации, равна высоте, эквивалентной одной, единице переноса, умноженной на ступень изменения концентрации,; или
|
|
|
H |
|
Т |
|
■у С |
|
VЕ |
|
Ф\ |
(3—56)
|
|
Определение теоретического числа ступеней изменения концентрации графическим методом. В тех случаях, когда равновесная зависимость
Является более сложной и линия равновесия представляет собой кривую, определяемую уравнением Рауля-Дальтона или эмпирическим путем, аналитическая зависимость для числа ступеней изменения концентрации не является такой простой, как при линейной равновесной зависимости.
Однако во всех случаях массообмена, т. е. при любой равновесной зависимости, число ступеней изменения концентрации можно сравнительно просто определить графическим путем на диаграмме у—х.
Для этого на диаграмме у—х наносят прямую в случае линейной равновесной зависимости (рис. 321) или кривую равновесия в случае
|
Рис. 322. Определение числа ступеней изменения концентрации в случае криволинейной равновесной зависимости. |
|
Рис. 321. Определение числа ступеней изменения концентрации в случае линейной равновесной зависимости. |
|
-л- Ш |
|
|
Любой другой равновесной зависимости (рис. 322) и прямую рабочих концентраций по уравнению у=Ах+В. Проводя из точки а, соответствующей конечной концентрации компонента, распределяемого между фазами, горизонтали и вертикали между линией равновесия и линией рабочих концентраций, получаем ломаную линию. Число ступеней этой ломаной и будет числом ступеней изменения концентраций Nc. Так, на рис. 321 Nc=2 и на рис. 322 Nc= 5.
В случае линейной равновесной зависимости согласно уравнению (3—51) число единиц переноса mvC, соответствующее одной ступени измене ния концентрации, не зависит от концентрации и для каждого конкретного случая является величиной постоянной, зависящей от наклона
K
Прямой равновесия п= В этом случае все ступени изменения кон -
Центрации являются равноценными и высота hvc, эквивалентная одной ступени изменения концентрации, численно одинакова для всех ступеней.
Высота насадки Н в этом случае может быть определена как
H = hycNc (3—57)
Если равновесная концентрация не является линейной и линия равновесия представляет собой кривую, такой простой зависимости между числом ступеней изменения концентрации и высотой насадки нет. В этом случае эквивалентные одной ступени число единиц переноса для отдельных ступеней изменения концентрации и высоты не одинаковы и зависят
от состава фаз для каждой данной ступени изменения концентрации. Поэтому общая высота насадки определяется равенством
H = Hl т1 - j- /г11 т11 Н------------------------------------------ (3—58)
Ус ус 1 ус ус 1 V , >
ИЛИ
"с
H = ^hyzmyc (3-59)
І
Однако число ступеней изменения концентрации Nc и в этом случае может быть определено графически путем построения на диаграмме у—х ломаной линии между кривой равновесия и линией рабочих концентраций, как это было показано на рис. 322.