АППАРАТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ
Теплопередача при постоянных температурах
Тепловой поток, возникающий вследствие разности температур, является обычно результатом одновременного действия всех трех видов - теплопередачи: теплопроводности, теплового излучения и конвекции.
Суммарная теплоотдача лучеиспусканием и конвекцией. В тех случаях, когда теплообмен происходит между твердым телом (стенкой) и газообразной средой, в расчетах необходимо учитывать одновременно с передачей тепла путем конвекции также и тепловое излучение.
|
<р |
Как известно, количество тепла, отдаваемого твердым телом путем теплового излучения,^ определяется по уравнению (2—23):
ТУг. \4 ( тж у 100 ) ^ 100 у
|
|
Тег. У ( Тж \4]
<Р (t„. — гж)
|
|
Примем обозначение
|
|
Тст. у ( Тжуі
|
? = ал |
100 У 100 J J
^Рт. І У
|
|
Тогда
|
|
Qn = АЛ^х (*СТ. — їж) Ккал
Т. е. получаем уравнение теплового излучения, аналогичное основному уравнению теплоотдачи. Это уравнение называют также уравнением прямой отдачи тепла, а величину ал—к оэффициен - том прямой отдачи, который показывает, какое количество тепла отдает окружающей среде за счет теплового излучения стенка поверхностью Хм2, за время 1 ч а с при разности температур 1°С. Коэффициент ал имеет таким образом размерность:
Г ,___ Г ккал "j
|
Или |
* [м*.час'°CJ
Суммарная отдача тепла поверхностью стенки одновременно путем конвекции и теплового излучения равна
Q = Qk + <2л = aKf~ (tcr. — *ж) + ал (tcr. — U
Q = (ак + Ссл)і7т(/ст> /ж)
Обозначив ак+ал=а, получим уравнение теплоотдачи
Q = a, Ft (^ст. — ккал (2—77а)
|
(2—77) |
Где а-—коэффициент теплоотдачи за счет конвекции и теплового излучения в ккал! м2- час °С. Уравнение теплопередачи при постоянных температурах для плоских стенок. Обычно при расчете процессов теплообмена известна не температура стенки, а температура той среды, которая окружает стенку и с которой происходит теплообмен. В этом случае задана температура
Окружающей среды для обеих сторон стенки и необходимо найти, какое количество тепла в час, передается через стенку от более нагретой среды к менее нагретой и температуру поверхностей стенки. ]
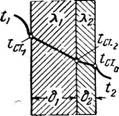
Рассмотрим сложную стенку, состоящую из двух слоев с различной теплопроводностью (например, стенка котла и котельная накипь на ней), и примем обозначения (рис. 213):
—температура более нагретой жидкости; t.2—температура менее нагретой жидкости; ах—коэффициент теплоотдачи от более нагретой
Жидкости к стенке; а2—коэффициент теплоотдачи от стенки к менее
Нагретой жидкости; ох—толщина первого слоя стенки; 82—толщина второго слоя стенки; \—теплопроводность первого слоя стенки; Х2—теплопроводность второго слоя стенки; F—поверхность стенки;
Q—количество тепла, проходящее через сложную стенку;
4т. і—температура поверхности стенки со стороны более нагретой жидкости;
4т. а—температура поверхности соприкосновения двух слоев сложной стенки;
4т.-2—температура пЪверхности стенки со стороны менее нагретой жидкости.
Расчет теплопередачи проводим, исходя из того, что при установившемся состоянии процесса за время х одно и то же количество тепла:
1) переходит со стороны более нагретой жидкости на поверхность стенки;
2) проходит сквозь сложную стенку;
3) переходит по другую сторону стенки с ее поверхности к менее нагретой жидкости.
Количество тепла, переходящее от более нагретой жидкости' к стенке, через стенку и от стенки к менее нагретой жидкости, можно найти из следующих уравнений:
Q = AtFx (іг — Істл); Q = Fx (і„л — TCTM)
Q = (4T-a — 4t.2); Q = a2Fx (t„,t —4) Если написать эти четыре уравнения в виде:
Q ^ = Fx <v - 'crj; Q= ^ (4т. х - 4т J qА-=Fx (tCT. a - 4t.2); = (t„mt-12) и сложить их, то получим
Или
|
Рис. 213. К выводу уравнения теплопереда: Чи Через п лоску кг - стенку. |
Ax + A2 2J x
Q^KFt^-Q (2-79)
Это выражение является уравнением теплопередачи для плоской стенки при постоянных температурах.
Величину К = - j---------------------- ^ s называют коэффициентом
Теплопередачи.
При F= 1 м\ —4)=1° и час
О=к\ Ккал ]
Коэффициент теплопередачи /С показывает, какое количество тепла проходит за время 1час от более нагретой жидкости к менее нагретой через разделяющую их стенку поверхностью 1 jw2 п р и разности температур между жидкостями в 1°.
|
[К] = |
Таким образом, размерность К:
Ккал 1 !.«шс.° Cj
Зная толщину стенки, ее теплопроводность и коэффициенты теплоотдачи по обеим сторонам стенки, можно из уравнения (2—78) найти коэффициент теплопередачи при заданных условиях.
По коэффициенту К можно вычислить количество тепла, передаваемого через стенку от более нагретой жидкости к менее нагретой.
Величина, обратная К, называется термическим сопротивлением и имеет размерность м2- час -°С/ккал.
Если в уравнении
К 1
Ot, ^ cta 2j X
А4
Написать в правой и левой части обратные величины, то получим
X ^ +
Где — термическое сопротивление теплопередачи;
~ и А---------- термическое сопротивление теплоотдачи;
----- термическое сопротивление собственно стенки.
|
Введя обозначение |
|
1 і Vі |
|
= К \ / (2-78) |
|
Получим |
Когда теплообмен происходит между загрязненными или химически активными жидкостями, отлагающими осадок на поверхности теплообмена, то при определении величины К следует учитывать термическое сопротивление слоя загрязнений, которое значительно превышает терми
ческое сопротивление собственно металлической стенки. В случае отсутствия опытных данных учитывают толщину слоя загрязнений ориентировочно, принимая ее равной 0,1—0,5 мм.
Уравнение теплопередачи при постоянных температурах для цилиндрических стенок. На практике наиболее часто в качестве поверхностей иагрева используют трубы.
Рассмотрим цилиндрическую стенку (см. рис. 201), по одну сторону которой, например внутри цилиндра, находится более нагретая жидкость с температурой tlt а по другую (наружную)—менее нагретая жидкость с температурой t2.
Обозначим: гв—внутренний радиус цилиндра; /*н—наружный радиус цилиндра;
Ав—коэффициент теплоотдачи для внутренней поверхности стенки; ан—то же, но для наружной поверхности стенки; L—длина цилиндра.
При установившемся состоянии процесса одно и то же количество тепла должно за время т:
1) переходить от более нагретой жидкости к внутренней поверхности стенки;
2) проходить через стенку;
3) переходить от внешней поверхности стенки к менее нагретой жидкости.
Соответственно получим три уравнения:
Q = ABFBx (Tj — TCT. г) = Agitrjbz (Tx — /Єт. г)
|
|
|
(4т. |
|
Q |
Q—-------------------- (4т. і 4т. 2)
|
|
![]() 'в
'в
Q = АН^нх (4т. 2 — 4) = Ан2тггнІт (/ст.-2 — T2)
|
|
Или, преобразовывая
|
|
Q -—- = 2т: Lx (tx — tcT. x)
АвГ в
Q± 2,3 lg ^ = - 4t.2)
|
« |
Л Гв
Q —7- = 2ttLT (/ct>2 —12)
Сложив правые и левые части уравнений, получим
|
|
|
|
Откуда:
|
|
|
2TcLT (іг — T2) |
|
KR = |
|
АВ? в Введя обозначение |
|
|
Получим
|
|
|
(2—79а) |
Q = KRLz(T1-T2)
При L— 1 м, т=1 час. и /j —/2=1
Q = К« Г-™"
Чоо°С J
Таким образом, Kr представляет собой коэффициент теплопередачи цилиндрической стенки, показывающий, какое количество тепла передается за час от одной жидкости к другой через цилиндрическую стенку длиной Іліпри разности температур в 1°.
Следовательно, размерность Kr:
Вместо применения уравнения Q=KRLi(t1—1.2), неудобного для вычислений, можно расчеты теплопередачи в трубах вести так же, как для плоской стенки с толщиной, равной
А = fa-гв)
Причем плоская стенка должна иметь то же термическое сопротивление, что и цилиндрическая.
Применяя этот метод, приравниваем уравнения теплопередачи для плоских и цилиндрических стенок:
Q = KFz (іг — /,) = KR Lx {Tx -12)
Или
KF = KrL
Подставив в полученное уравнение значения К и Kr, а вместо F
Ее величину 2ъгс{)Ь (где лср.—средний радиус трубы), получим
1 = 2,1
J _L А р" 1 1 _L SiІ
Тв+аь+ X авгв * «нгн ^ X 2'31G ГЕ
Откуда
І 1
— —
■v= л-------------- її-,. <2-8°)
------- a--------- - т-г. зір—
«b'b т «нгн т і ' ё гв
По среднему радиусу гср., вычисленному из уравнения (2—80), находим величину поверхности F=2wc„ L некоторой плоской стенки, сопротивление теплопередаче которой будет равно сопротивлению цилиндрической стенки (трубы) той же толщины.