АППАРАТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ
Теплопередача
Химические процессы протекают в большинстве случаев в заданном направлении только при определенной температуре, которая достигается путем подвода или отвода тепловой энергии.
Теплообмен имеет исключительно важное значение для проведения процессов выпаривания, перегонки, сушки и многих других. Процессы, скорость протекания которых определяется скоростью подвода или отвода тепла (нагревание, охлаждение, выпаривание и др.)» называются тепловыми процессами.
Теплообмен между телами может протекать самопроизвольно или с затратой механической работы. Тепло передается без затраты работы извне только от тел с высшей температурой к телам с низшей температурой. Это положение является основным для осуществления передачи тепла, так как согласно второму закону термодинамики переход тепла, от тела с низкой температурой к телу, обладающему более высокой температурой, без затраты механической энергии невозможен.
В технологических процессах требуется или возможно лучшая теплопередача или, наоборот, возможно лучшее предохранение тел от теплообмена. К первому случаю относится передача тепла в нагревательных и холодильных устройствах, а ко второму—защита от потерь тепла или изоляция для предотвращения термического воздействия.
Переход тепла из одной части пространства в другую может происходить действием теплопроводности, излучением и конвекцией.
Теплопроводность. Этот вид теплообмена возможен в условиях тесного соприкосновения между отдельными частицами тела и заключается в том, что тепловая энергия распространяется внутри тела от одной частицы к другой, соседней, находящейся в непосредственной близости, вследствие их колебательного движения. Частицы более нагретой части тела, сталкиваясь при колебательном движении с соседними частицами, сообщают им часть своей кинетической энергии, и таким образом тепловая энергия распространяется по всему телу. Этот процесс будет происходить до тех пор, пока не наступит полное равенство температуры во всем теле.
Тепловое излучение. При теплообмене излучением тепло распространяется в виде лучистой энергии. Выделяющееся тепло превращается в лучистую энергию, которая распространяется в пространстве, и в каком-нибудь другом месте полностью или частично превращается вновь в тепловую энергию.
Конвекция. Под конвекцией понимают перенос тепла частицами капельных жидкостей и газов путем их перемещения из одной части пространства в другую. Это происходит при движении капельных жидкостей и газов, которое возникает либо вследствие различия
Удельных весов в разных точках их объема (из-за неравномерности температур в нем), либо в результате механических воздействий извне.
Практически виды теплообмена редко наблюдаются раздельно; в большинстве случаев они связаны между собой и проявляются одновременно.
Сложный процесс перехода тепла от более нагретой жидкости к менее нагретой через разделяющую их стенку носит название теплопередачи.
50. Теплопроводность]
Температурное поле и температурный градиент. Необходимым условием распространения тепла является неравенство температур в различных точках данного тела или пространства. Поэтому величина теплового потока, возникающего в теле вследствие теплопроводности, зависит от распределения температур в теле, или характера температурного поля (под температурным полем понимают совокупность мгновенных значений температур в рассматриваемом теле или пространстве).
Температура в какой-нибудь точке тела является функцией положения этой точки и времени. Поэтому математически температурное поле определяется функциональной зависимостью
T = F(X, у, г, т)
Где t—температура данной точки:
Х$ У, z—координаты данной точки; т—время.
Геометрическое место всех точек с одинаковой температурой представляет собой изотермическую поверхность. Все изотермические поверхности различных температур в одном и том же теле не пересекаются друг с другом, в противном случае линии их пересечения обладали бы различными температурами. Поэтому все изотермические поверхности замыкаются или кончаются на границах рассматриваемого тела.
При перемещении из любой точки вдоль по изотермической поверхности изменение температуры не обнаруживается. Наоборот, вдоль какого-либо направления, пересекающего изотерму, температура изменяется, причем изменение будет наибольшим в направлении, нормальном к изотермической поверхности.
Предел отношения разности температур М двух близких изотермических поверхностей с температурами / и t-\-At к расстоянию по нормали Д/г между ними, т. е.
Hm[*-1 (2-1)
Называют температурным градиентом.
Температурный градиент, численно равный изменению температуры на единице длины нормали к изотермической поверхности, является мерой интенсивности изменения температуры в данной точке.
Тепловой поток в теле наблюдается только тогда, когда температурный градиент во всех точках тела не равен нулю; направление потока всегда совпадает с направлением падения температуры в данной точке.
Закон Фурье и коэффициент теплопроводности. Величина теплового потока Q, возникающего в теле вследствие теплопроводности при некоторой разности температур в отдельных точках тела, определяется по эмпирическому закону Фурье.
Согласно этому закону элементарное количество тепла dQ, проходящее через элемент изотермической поверхности dF за промежуток
Времени dt, пропорционально температурному градиенту, величине поверхности и времени, т. е.
DQ = — >, dF d% ккал (2—2)
Где Q—количество тепла в ккал\
X—коэффициент пропорциональности, который называют коэффициентом теплопроводности или просто теплопроводностью; п—расстояние в м;
F—поверхность, нормальная к направлению теплового потока, в ж2; т—время в часах.
Знак минус, стоящий в правой части уравнения, показывает, что тепловой поток изменяется в сторону уменьшения температуры.
Физический смысл и размерность коэффициента теплопроводности а вытекают из уравнения (2—2), если его решить относительно X:
М-час-°С
Таким образом, коэффициент теплопроводности показывает, какое количество тепла (вккал) проходит вследствие теплопроводности через I ж2 поверхности за время I час при разности температур в 1°С, приходящейся на J л длин ь^ н о р м а л и к и 3jlt ермической поверхности.
Коэффициент теплопроводности "выражает способность вещества проводить тепло и, следовательно, является физической характеристикой этого вещества. Числовое значение X зависит от состава вещества и может быть определено только опытным путем; оно колеблется в широких пределах и составляет:
Для теплоизоляционных материалов от 0,02*до 0,1 ккал/м-час-°С » строительных материалов. . » 0,5 » 3,0 »
» металлов.......................... » 2 » 360 »
Коэффициент теплопроводности твердых тел. Коэффициенты теплопроводности твердых тел значительно разнятся друг от друга. Так, например, для некоторых металлов, применяемых в химическом аппарато - строении, л имеет следующие средние значения (в ккал! м-час-°С)'. медь 330; алюминий 175; чугун 54; углеродистая сталь 40; свинец 30; нержавеющая сталь 20. Теплопроводность металлов сильно зависит от их состава и содержания примесей.
Коэффициент теплопроводности данного тела зависит от температуры; для большинства однородных твердых тел эта зависимость л от температуры приблизительно линейна и может^быть выражена равен-* ством
X^Xo(l-fW) (2—3)
Где X—коэффициент' теплопроводности для данного твердого тела при данной температуре (/°С);
Х0—коэффициент теплопроводности для того же тела при 0°С;
B—температурный коэффициент, являющийся для большинства твердых тел положительной величиной.
Коэффициент теплопроводности жидкостей и газов. Коэффициенты теплопроводности капельных жидкостей и газов значительно
Меньше коэффициента теплопроводности твердых тел. Например, при комнатной температуре коэффициент теплопроводности воды равен 0,51 ккал! м-час-°С, спокойного воздуха —0,02 ккал/м-час °С, в то время как коэффициент теплопроводности углеродистой стали равен 40 ккал! м-час-°С.
Коэффициенты теплопроводности большинства жидкостей в отличие от твердых тел уменьшаются с возрастанием температуры; исключением являются лишь вода и глицерин, теплопроводность которых с повышением температуры возрастает. •
|
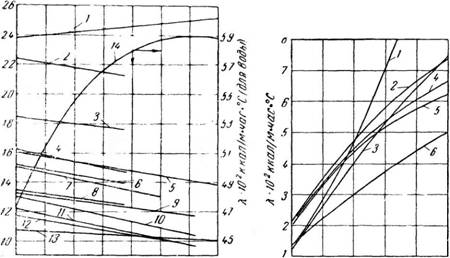
Рис. 196. Теплопроводность капельных жидкостей: Рис. 197. Теплопроводность газов: |
|
І І |
|
|
/—глицерин безводный; 2—муравьиная кислота 3—метило - 1—водяной пар; 2—кислород; 3—углекис - вый спирт; 4—этиловый спирт; 5—анилин; в—уксусная кис - лота; 4—воздух; 5—азот; в—аргон лота; 7—ацетон; <5—бутиловый спирт; 9—нитробензол; 10—бен - (10 X =Х ) зол; 11—толуол; 12—ксилол; 13— вазелиновое масло; 14—вода Аг 1-12 s (масштаб справа).
В капельных жидкостях и газах всегда наблюдается явление конвекции, сопровождающееся передачей тепла вследствие взаимного перемещения частиц; это осложняет определение коэффициентов теплопроводности.
Значение коэффициента теплопроводности X для капельных жидкостей можно определить расчетным путем по формулам А. С. Предводи - телева и Н. Б. Варгафтика:
1 = £СРї Vir ккал/м• час-°С (2—4)
Ої. О
Где Ср—теплоемкость жидкости в ккал/кгс-°С.
У—уд. вес жидкости в кгс/м3;
М—молекулярный вес жидкости;
Для неассоциированных жидкостей (бензол, толуол и другие углеводороды) є=1,55- Ю-4; для ассоциированных жидкостей (вода, спирты и др.) s=l,29-Ю-4.
Значения Х=/(/) для капельных жидкостей, по экспериментальным данным Н. Б. Варгафтика (Всесоюзный теплотехнический институт), приведены на рис. 196.
Коэффициент теплопроводности газов возрастает с повышением температуры и практически мало зависит от давления.
Значения Х=/(0 для газов могут быть определены по графику (рис. 1І97). Для приближенных технических расчетов пользуются формулой
•-4-WЈ)(M)F <2"4а>
Где С—опытная постоянная, значение которой для некоторых газов приведено в табл. 10.
|
Fiztdl |
|
№ |
|
-A |
Таблица 10
|
Значение величины С
|
В технических расчетах обычно принимают средние значения коэффициента теплопроводности, считая его во время процесса теплопередачи постоянным.
Дифференциальные уравнения теплопроводности. Выделим в однородном и изотропном теле элементарный параллелепипед объемом dV с ребрами dx, dy, dz (рис. 198) и будем считать, что физические свойства тела—удельный вес (у), теплоемкость (с) и теплопроводность (X)—одинаковы в каждой точке параллелепипеда и не изменяются во времени.
Количество тепла, входящего в параллелепипед через его грани за промежуток времени dz, определяется уравнениями: по оси х—через грань dy dz
Qx — — "к-^- Dy Dz Dz
Qx+Dx
Dx
По оси у—через грань Dx Dz Qy = — L-J^Dxdz Dz
По оси z—через грань dx dy
Dt
Qz = — L~ Dxdydz
За тот же промежуток времени через противоположные грани из параллелепипеда выйдет тепло в количестве:
По оси х 0
Qx+dx = — K^Dydzdz + J—J Dx^Y ^ Dzj По оси у
Qy+Dy = -L^Dxdzdz -L^-^Dydxdzdzj По оси Z
|
Ay* |
|
Dy |
|
Чг |
|
Рис. 198. К выводу дифференциального уравнения теплопро - |
Qz+dz =-I ^ Dx D У Dz + ^-X^^Dz Dxdydz]
Разность между количеством тепла, введенным в параллелепипед за промежуток времени dz и вышедшим из него за тот же промежуток времени, определяется равенствами: по оси х
ДЧ
DQx =-Qx — Qx+Dx = л Dx Dy Dz Dx
По оси у
ДЧ
DQy = Qy — Qy+Dy = X -ф - Dx Dy Dz Dz
ПО ОСИ 2
ДЧ
DQz = QZ — Qz+Dz = ^ - - p- Dx Dy Dz D-Z
Полное приращение тепла в параллелепипеде за промежуток времени dz: |
DQ=DQx + DQy+DQz
Или
^ = + + Dxdydzdz (2—5)
Заменив произведение dx dy dz его значением dV, получим
ДЧ. дЧ, дЧ
Л / дч, дЧ. \ л\т л
ГВыражение, стоящее в скобках'последнего уравнения, представляет собой оператор Лапласа, т. е.
ДЧ дЧ^ , дЧ __ 2, дх2 + ду*
И, таким образом,
DQ = ly4dVdz (2—6)
По закону сохранения энергии приращение количества тепла в параллелепипеде должно равняться количеству тепла, расходуемому на изменение теплосодержания рассматриваемого^параллелепипеда, т. е.
DQ = су DV~ Di ' (2—7)
Где —изменение температуры параллелепипеда за^промежуток
Времени drJk
Приравнивая друг другу уравнения (2—7) и J2—6), получим cydV — dt^X^mVdx.- или (после сокращений 'и введения обозначения а= -^-получим
Dt =ауН / (2-8)
Dz
І S
Выражение (2—8) является дифференциальным *у равнением теп лопроводности в неподвижной среде, или уравнением Фурье. Оно позволяет определить распределение температур в любой точке тела, через которое проходит тепло вследствие теплопроводности.
Коэффициент пропорциональности а=— в уравнении Фурье носу
Сит название коэффициента температуропроводности и имеет размерность:
Ккал
|
|
|
I Сг |
|
М* |
|
(2-9) |
|
\а] = |
|
Кгс |
М>час<°С
Ккал
L Кгс .°С м3 J
|
|
Коэффициент температуропроводности а является физической величиной и характеризует собой теплоинерционные свойства тел. При прочих равных условиях быстрее нагреется или охладится то тело, которое обладает большим коэффициентом температуропроводности.
Если в процессе теплопроводности не происходит изменения температуры со временем, т. е. это означает, что процесс является установившимся и уравнение (2—8) в этом случае принимает вид:
А^Н =» О
А отсюда, так как а не может быть равным нулю
|
ДЧ Dz2 |
|
О |
|
(2-10) |
Vа/ = О
Или
ДЧ дЧ_
Дх2 +
Уравнение (2—10) является дифференциальным уравнением теплопроводности в неподвижной среде при установившемся тепловом режиме.
Дифференциальные уравнения (2—8) и (2—10) определяют передачу тепла теплопроводностью в самой общей форме, без учета форм тела, через которое проводится тепло, свойств тела и свойств окружающей среды, т. е. эти уравнения описывают только класс явлений теплопроводности. Конкретные условия теплопроводности для того или иного частного явления можно установить, если задать граничные условия, характеризующие данное явление.
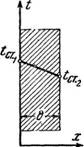
Теплопроводность плоской стенки при установившемся тепловом потоке. Рассмотрим теплопроводность плоской стенки (рис. 199), длина и ширина которой безгранично велики' по сравнению с ее толщиной; ось х расположена по нормали «к поверхности стенки.
Обозначим температуру наружных поверхностей стенки через ^ст. і и ^ст.2» причем ^ст. х>^ст.2 При установившемся процессе количества тепла, подведенного к стенке и отведенного от нее, должны быть равны между собой и не изменяться во времени.
|
Рис. 199. К выводу уравнения теплопроводности плоской стенки. |
На основании дифференциального уравнения теплопроводности распределение температур только вдолъ оси х представится в виде:
|
|
|
ДЧ Дх2 |
|
= 0 |
(2-11)
|
|
Интегрирование этого уравнения приводит к функции
/ = Cxx-HC2 (2—12)
Где СЛ и С2—константы интегрирования.
Уравнение (2—12) показывает, что по толщине плоской стенки температура изменяется прямолинейно.
Константы интегрирования можно определить, приняв соответствующие граничные условия:
Если х=0, то t=tCT. i и уравнение (2—12) примет вид
Если х=0, ТО T=Tcr.2 и
Или
Откуда
Подставив значения констант Сх и С2 в уравнение (2—12), получим
|
Рис. 200. К выводу уравнения теплопроводности плоской стенки. |
|
В ккал! м- час °С; |
T = X+V,
Откуда
Dt 'ст. 2 ^CT. J
Dx о
Подставив найденное значение температурного градиента в уравнение теплопроводности (2—2), получим
DQ = — \ *С1' 2~ tcr~ dF4t
Или
Q ~ у (^ст-! — *ст. а) ^ кяал (2—13)
Где к—теплопроводность материала стенки
8—толщина стенки в м\ tст. і—^ст.2—разность температур наружных поверхностей стенки в °С; F—поверхность стенки в М2-, і—время в час.
■ Уравнение (2—13) является уравнением теплопроводности плоской стенки при установившемся состоянии процесса теплообмен
Если стенка составлена из п слоев, отличающихся друг от друга теплопроводностью и толщиной (рис. 200), то при установившемся состоянии процесса через каждый слой стенки пройдет одно и то же количество тепла и могут быть составлены следующие уравнения:
Q = (4т., - и Fx Или Q А = (T^ - Ta) Fx Q=}I~{Ta-Tb)Fx Или Q^ = {Ta-Tb)Fx
Q = T-(Tn-T„.9)Fx Или QliL={Tn-TCT.2)Fx
Складывая правые и левые части этих уравнений, получим
|
|
Откуда
|
|
Q =-- H^Z—-— ккал
Ег
1=1
Где і—порядковый номер слоя стенки; п—число слоев.
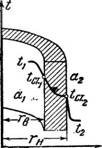
Теплопроводность цилиндрической стенки при установившемся тепловом потоке. Пусть внутренняя и внешняя поверхности цилиндрической стенки (рис. 201) имеют постоянную температуру t
Ст. X
Обозначим: гв—внутренний радиус стенки; гн—наружный радиус стенки; г—текущий радиус стенки; L—длина стенки;
X—теплопроводность материала стенки.
|
(2-14) |
|
Рис. 201. К выводу уравнения теплопроводности цилиндри - • ческой стенки. |
Вследствие того что внутренняя поверхность цилиндрической стенки, равная 2nrBL, меньше ее наруж - X ной поверхности 2тгrHL, уравнение (2—13) здесь неприменимо.
|
Q |
Пользуясь уравнением (2—2), можно написать
\2KLTZ
Dt>
Так как здесь 8=гн—гв, то вместо do можно подставить dr,
|
|
|
Тогда |
|
CU Dr |
Q = — Х2тг Lrz
|
|
Или
Интегрируя это уравнение в пределах от внутреннего радиуса до наружного, получим
Г Dr_________ 'Шл п
|
At |
J « J
Или
^ RH 12TZLZ (ІСт. о — TcT.F)
Q
Откуда
|
|
2тZLz (^Ct.J — TCT.Z)
|
(2-15) |
|
Q |
|
Ккал |
4-2,3
|
|
Это и есть уравнение теплопроводности для цилиндрической стенки.
По аналогии с выводом, приведенным для однослойной стенки, можно для н-слойнЬй цилиндрической стенки написать следующую формулу!
2tiLZ (tcT.1 ^ст. о) /0
Q — г^----------- І-------- — ккал (2—16)
V 1 о Її, R*+I
T"=l
Где і—порядковый номер слоя стенки.
Теплопроводность при неустановившемся тепловом потоке. В случае, если при Нагревании или охлаждении температурное поле меняется во времени, необходимо определить зависимость изменений температуры и количество переданного тепла во времени для любой точки тела. Эта задача представляет большой интерес для тепловых расчетов некоторых периодических процессов химической технологии, для расчета нагревательных печей и др.
Как было показано выше, дифференциальное уравнение теплопроводности для неустановившегося теплового потока имеет вид:?
Дії
Решение этого уравнения при наличии граничных условий требует применения сложной методики интегрирования; ниже приведены лишь результаты интегрирования В форме, удобной для решения практических задач.
Рассмотрим неустановившийся процесс теплопроводности для плоской стенки (плиты), цилиндра и шара. С этой целью введем понятие избыточной температуры и избыточного тепла. Избыточная температура © представляет собой температуру, отсчитанную от температуры среды, окружающей изучаемое тело, как от нуля. Избыточное тепло Q представляет собой теплосодержание, измеряемое при избыточной температуре 0.
Примем обозначения:
©о—начальная избыточная температура в каждой точке тела в °С; ©ср.—конечная избыточная температура в средней плоскости стенки, по оси цилиндра или в центре шара в °С; ©ст.—конечная избыточная температура на поверхности плоской стенки, цилиндра или шара в °С;
Qo—начальное избыточное теплосодержание тела в ккал;
Q —конечное избыточное теплосодержание тела в ккал\
Х—время нагревания или охлаждения тела в часах; *ст.—коэффициент теплопроводности тела в ккал/час-°С;
А—коэффициент теплоотдачи (см. стр. 300), учитывающий отдачу тепла наружной поверхности тела в окружающую среду, в ккал/м2'час»°С;
« 1
H— у—коэффициент с размерностью — ;
А—коэффициент температуропроводности в мг/час',
I—величина, характеризующая линейный размер тела, в м.
Для цилиндра и шара I — радиус в м, для плоской стенки (плиты) I при одно -
\ 6 стороннем обогреве равен толщине\стенки о в ж, а при двустороннем обогреве I— .
Решение дифференциального уравнения теплопроводности для неустановившегося теплового потока может быть представлено для тел любой формы в виде функции от трех безразмерных комплексов
А/ ах х
Т"' ' Т
Эти комплексы получаются из совместного решения приведенного выше уравнения теплопроводности и уравнения Ньютона (стр. 303) и являются критериями подобия. At
Критерий -у носит название критерия Нуссельта
;Гі
-у = Ми
•9 А. Г. Касаткин.
Критерий - р называется критерием Фурье:
Ат
-J,T = Fo
И, наконец, является критерием геометрического подобия.
В большинстве случаев достаточно знать температуру 0СТ. тела на поверхности и 6ср. в середине (или средней плоскости) тела. Если эти температуры известны, то от -
X
Ношение — =L становится постоянным (при х— 0 величина 1=0 или при х=8 величи на 1=1). Поэтому искомая функция может быть выражена зависимостью
= Ф (Nu, Fo) (2—17)
"о-
Эта функция может быть представлена для каждого из трех рассматриваемых тел в случае их охлаждения в следующем виде:
Для избыточной температуры в средней плоскости стенки (плиты), по оси цилиндра или в середине шара
А/ ах
= 72-) <2-|8>
"0
Для избыточной температуры на поверхности
Al
F Al Ат\
"о
Для величины переданного тепла
О I Al Ах\
= ~W) <2-18б>
В случае нагревания тел перед правой частью уравнений (2—18), (2—18а) и (2—186) ставится знак минус.
Значения функции Ф(Nu, Fo) для плоской стенки, цилиндра и шара приводятся в виде таблиц и графиков в специальных курсах по теплопередаче[2].
Зная физические свойства изучаемого тела, его геометрическую форму и размеры, а также продолжительность нагревания или охлаждения, можно при помощи диаграмм определить количество переданного тепла и установить изменение температуры тела.