АППАРАТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ
Основные уравнения движения жидкостей
Уравнение неразрывности потока. При установившемся движении жидкости по закрытому трубопроводу и отсутствии утечки через неплотные соединения через каждое поперечное сеч ение трубопровода в единицу времени протекает одно и то же весовое количество жидкости. Это явление характеризуется так называемым уравнением неразрывности или сплошности потока.
Для трубопроводов с разветвлениями уравнение. неразрывности
Относится соответственно к сумме отдельных разветвляющихся потоков.
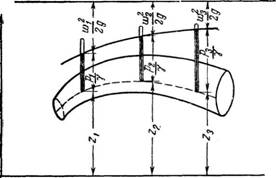
Обозначим (рис. 6): Gv G2, G3—вес жидкости, протекающей в секунду соответственно через сечения /—/, 2—2 и 3—3 в кгс; її» Ї2> Тз—УД- вес жидкости в тех же сечениях в кгс/м3\ fv /2» h—поперечные сечения трубопровода в м2\ ' wv w2, w5—средние скорости протекания жидкости через указанные
|
Л |
|
І |
|
4- - |
|
Рис. |
|
6. К выводу уравнения неразрывности потока. 1—3—сечения трубы. |
Выше сечения трубопровода в м/сек. Тогда уравнение неразрывности потока может быть выражено так:
|
(1-22) (1—22a) |
|
Const |
|
ИЛИ |
Gx = G.2 = G3
/і^іТі = 2Ї2 = /з^зїз =Iconst
Для несжимаемых (капельных) жидкостей, удельный вес которых остается неизменным по длине трубопровода, уравнение неразрывности принимает следующий вид:
Fxwi = />2 = /а = const
При неустановившемся движении жидкости, как уже указывалось выше, физические ее характеристики непрерывно изменяются во времени.
Уравнение неразрывности потока для неустановившегося движения сжимаемой жидкости может быть сформулировано следующим образом: изхменение массы жидкости, заключенной в данном объеме и проходящей через каждое попере ч- ное сечение трубопровода, происходит только за счет изменения ее плотности в этом объеме.
|
(1-23) |
Уравнение неразрывности потока для неустановившегося движения жидкости выражается в дифференциальной форме:
|
(1—23а) |
|
Dz |
|
Дт |
|
Дх |
D(p^) д (ра»у) д (owz) = q
Ду
Если рассматривается установившееся движение, то р не зависит
Л
От времени Qjz=0) и уравнение (1—23а) принимает вид:
|
Д (Pay) , Д (рWz) Ду Dz = и |
|
Д (раь) Дх |
|
(1—236) |
Если жидкость несжимаема, то плотность ее по длине трубопровода (в направлении осей dx, dy, dz) также не изменяется, и уравнение неразрывности потока будет выражаться так:
Dwy
JY
Дх 1 ду 1 Dz
Dwv Dwz
-qJj-, —изменение скорости no направлениям соответствующих осей координат. Дифференциальные уравнения движения Эйлера. Выделим в идеальной жидкости, находящейся в движении, элементарный параллелепипед объемом dV, с ребрами dx, dy, dz (рис. 7).
Как и при выводе дифференциаль - (p+-&-dz)dxAy ного уравнения равновесия, найдем ' проекции действующих сил на элементар
Ный объем dV.
|
Dz |
|
Dy/ |
|
Pdxdy |
|
"У |
|
Рис. 7. К выводу дифференциальных уравнений движения Эйлера. |
Z Dz Ь P Dz
Умножив левые и правые части этих уравнений соответственно на dx, dy, dz, получим:
Dw j 1 Dp ,
W „ Dx =--------------- -f-dx
X dx p dx
Dw , 1 Dp A
Dw j . 1 Dp ,
Vz&rdz=-gdz-j -^dz
Сложив уравнения, получим:
Wx^dx+w^dy+wj^dz=-gdz dz} (1-26)
Слагаемые, стоящие в скобках правой части уравнения (1—26), представляют собой полный дифференциал dp:
А слагаемые левой части уравнения представляют собой полный дифференциал скорости, умноженный на скорость w (так как рассматривается установившееся движение жидкости):
Dw і і Dw , , Dw , ,
Wx-fodx + wy +wz-fodz = wdw
Произведя соответствующую замену в уравнении (1—26), получим
|
Dz + ± + *(£) = о (1—26а) |
Wdw = —у - — G Dz
Но wdw=d и, следовательно,
Разделив обе части последнего равенства на g и произведя замену og на у, получим
Или
2(1
При установившемся движении несжимаемой однородной жидкости y=const и сумма дифференциалов в уравнении (1—26а) может быть заменена дифференциалом суммы:
Откуда следует, что
І Р І w
|
Const |
|
(1-27) |
Т+ 2?
|
Величина Z-\-~- + W |
Полученное уравнение и есть уравнение Бернулли для идеальной жидкости, перемещающейся без трения, т. е. при отсутствии потерь напора (энергии).
|
|
|
Линия гидродинамического напора |
|
"Линия статического напора |
|
Ллосность сравнения |
|
Рис. . 8. Диаграмма Бернулли для идеальной жидкости при установившемся движения |
Называется гидродинамическим на-
7 ' 2g
|
К |
Пором. Гидродинамический напор складывается из следующих величин: г —н ивелирной высоты, называемой также геометрическим напором и представляющей собой высоту Ы] данной частицы жидкости относительно произвольно выбранной горизонтальной плоскости сравнения;
-статического или пьезометрического напора, равного давлению столба жидкости над рассматриваемый уровнем. Статический напор имеет размерность длины, так как
Р
Кг
_ Кг
-скоростного или динамического напора, который также имеет размерность длины, так как
W2 ___ Г м2
|
Сек' |
|
[м] |
2J | сек?
Таким образом, все члены уравнения Бернулли имеют размерность длины. Зависимость между ними наглядно изображается графически (рис. 8).
Выберем произвольно систему координат с горизонтальной плоскостью сравнения и определим давления и скорости для нескольких частиц идеальной жидкости, движущихся по траектории, изображенной на рисунке пунктиром. Для этого отложим от соответствующего положения каждой частицы отрезки соответственно ее геометрическому, статическому и скоростному напорам.
Соединив концы указанных отрезков, получим линии геометрического, статического и гидродинамического напоров, причем последняя линия будет лежать в горизонтальной плоскости. Это соответствует уравнению (1—27), по которому гидродинамический напор для частиц идеальной жидкости, движущихся по данной траектории, является величиной постоянной.
Уравнение Бернулли для невязкой жидкости, перемещающейся без трения, формулируется следующим образом: для любого сечения трубопровода, при установившемся дв иж е - нии идеальной жидкости, сумма скоростного и статического напоров и нивелирной высоты есть величина постоянная.
Уравнение Бернулли выражает частный случай закона сохранения энергии. Любой напор в трубопроводе можно рассматривать как энергию жидкости, отнесенную либо к 1 кгс, либо к 1 м3 жидкости.
|
|
|
|
Действительно
Т. е. давление или напор, выраженные в кгс/м2, представляют собой энергиюв кгс-м на 1 ж3 жидкости, а давление или напор, выраженные в м столба жидкости, представляют собой энергию в кгс-м на 1 кгс жидкости.
Поэтому в энергетической форме уравнение Бернулли для жидкости, перемешающейся без трения, может быть сформулировано следующим образом: для любого сечения трубопровода при установившемся движении невязкой жидкости сумма потенциальной ^z-Ь у j и кинетической
(^-j энергии жидкости, движущейся по трубопроводу, остается величиной постоянной.
При изменении сечения трубопровода и соответственно скорости движения жидкости происходит превращение энергии: при сужении трубопровода часть потенциальной энергии может перейти в кинетическую и, наоборот, при расширении трубопровода часть кинетической энергии может перейти в потенциальную причем общее количество энергии остается неизменным.
Таким образом, уравнение Бернулли является математической формулировкой закона сохранения энергии для невязкой жидкости при установившемся состоянии ее движения.
В технике приходится иметь дело не с идеальными, а с реальными жидкостями, т. е. такими, при движении которых возникают силы трения, обусловливаемые вязкостью жидкости, характером ее движения, трением о стенки трубы и т д. На преодоление возникающего сопротивления должна расходоваться некоторая часть энергии, и общее количе
ство энергии по длине трубопровода будет непрерывно уменьшаться за счет перехода потенциальной энергии в энергию, затрачиваемую на трение (энергию потерянную).
|
(1-28) |
В этом случае сумма членов уравнения (1—27) будет величиной постоянной только при учете потери энергии, т. е.
Ї+ ~ + г + ^п — const
Где hn—потеря энергии или потеря напора в м.
Уравнение (1—28) может быть сформулировано так: для любого сечения трубопровода, в котором протекает реальная жидкость, при установившемся движении, сумма напоров скоростного /гск., статического Лег., нивелирного z ипотерянного hn есть величина постоянная.
В случае протекания жидкости по горизонтальному трубопроводу, при установившемся движении, нивелирные высоты для всех сечений трубопровода будут одни и те же; следовательно, величина z из уравнения Бернулли может быть в этом случае исключена, и уравнение примет следующий вид:
|
(1-29) |
|
Const |
Ч ^ т ^ п
Для любого сечения горизонтального трубопровода, при установившемся движении жидкости, общий напор равен сумме скоростного, статического и потерянного напоров.
|
|
|
Рис. |
|
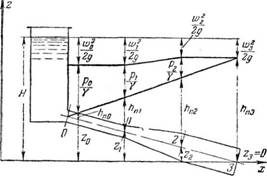
9. Диаграмма Бернулли для реальной жидкости. |
Применение уравнения Бернулли для реальных жидкостей можно иллюстрировать на примере движения жидкости по наклонному трубопроводу переменного сечения (рис. 9 и табл. 3). При установившемся движении жидкости общий гидродинамический напор И остается неизменным. Скоростной напор изменяется в зависимости от изменения сечения трубопровода—с увеличением сечения трубопровода скорость протекания жидкости уменьшается и соответственно уменьшается скоростной напор. Статический напор имеет максимальное значение в начале трубопровода (сечение О) и постепенно уменьшается вследствие увеличения потери напора. В отверстии, через которое происходит истечение жидкости, т. е. на конце трубопровода (сечение 3), статический напор равен нулю и ебніий гидродинамический напор равен сумме скоростного и потерянного напоров, т. е.
(1-30)
Таблица 3
Значения нивелирной высоты, статического напора, скоростного напора и потерянного напора в разных сечениях трубопровода (рис. 9)
|
Статический напор |
|
Скоростной напор |
|
Нивелирная высота |
|
Потерянный напор |
|
Сечение |
Верхний уровень жидкости в сосуде Сечение 0
Сечение 1 ............................................
Сечение 2 ............................................
|
Я |
|
О 2 Wj 2 Щ 2g |
|
О Y Рх_ Y Fh Y О |
Сечение 3 ............................................