АППАРАТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ
Основные факторы движения жидкостей
Перемещение жидкостей и газов по закрытым трубопроводам или каналам происходит под действием давления, создаваемого разностью уровней жидкости или работой насосов. Движение жидкостей и газов характеризуется рядом факторов, с рассмотрения которых и начнем изучение законов движения жидкостей.
Скорость протекания и расход жидкости. Рассмотрим движение жидкости по трубе постоянного сечения при условии, что жидкость заполняет все пространство внутри трубы.
Объем жидкости, протекающей через какое - либо поперечное сечение трубы в единицу времени, называют расходом жидкостии выражают его в м3/сек, л! сек или см3!сек.
В разных точках поперечного сечения потока скорость частиц жидкости неодинакова. Максимальная скорость наблюдается по оси трубопровода; чем ближе к стенкам, тем меньшей становится скорость частиц жидкости, и у самых стенок скорость их вследствие прилипания к стенкам равна нулю.
Однако можно допустить, что частицы жидкости имеют одинаковую скорость по всему сечению потока; такую условную скорость называют средней скоростью; ее можно найти как частное от деления объема жидкости, проходящего в
Единицу времени, на площадь поперечного сечения трубопровода или канала.
Обозначим: ^сек.—расход жидкости в м3/сек\
F—площадь поперечного сечения трубопровода в м2; w—средняя скорость протекания жидкости в м/сек.
Между этими тремя величинами имеются следующие зависимости
1/сек. = Wf МЧсек (1 — 16)*
F==Vce±_ м2
' W
W— Vce*' Ж! сек
Расход жидкости G, выраженный в кгс/сек, равен
G В= Wff Кгс/сек
Где уд. вес жидкости в кгс/м3.
На практике скорость протекания капельных жидкостей по трубопроводам составляет до 3 м/сек (для вязких жидкостей 0,5—1 м/сек). В нагнетательных трубопроводах скорость жидкости обычно равна 1,5—3 м/сек.
Скорости газов и паров значительно превышают скорости протекания капельных жидкостей и ориентировочно принимаются равными: для газов, находящихся под небольшим давлением, 8—15 м/сек, для газов под давлением 15—25 м/сек, для насыщенного водяного пара 20— 30 м/сек и для перегретого пара 30—50 м/сек.
Вязкость. Движение жидкости существенно зависит от ее вязкости, т. е. от внутреннего трения, которое проявляется при наличии относительного движения соседних слоев жидкости и зависит от сил сцепления между отдельными молекулами.
По закону Ньютона сила внутреннего трения, т. е. сила, проявляющаяся при перемещении одного- слоя жидкости относительно другого, прямо пропорциональна относительной скорости перемещения и величине поверхности соприкосновения этих слоев. Она зависит от свойств жидкости и не зависит от давления.
Обозначим: k — сила внутреннего трения;
F — поверхность соприкосновения слоев жидкости; w — скорость перемещения жидкости; п — расстояние между слоями движущейся жидкости.
Тогда. закон Ньютона выразится уравнением
K = (1-17)'
Где —коэффициент пропорциональности, зависящий от свойств жидкости и называемый коэффициентом вязкости или просто вязкостью;
ІЕ—приращение (производная) скорости, приходящееся на единицу длины расстояния между двумя слоями. Эта произво д- ная называется «градиентом скорости» по нормали.
Из уравнения закона Ньютона находим
|
F=4!=- о-!») |
K Dn F Dw
Принимая
F = 1 см2; п = 1 сж; од = 1 см/сек
Находим
= K
Т. е. получим значение абсолютной вязкости, выраженной в дн-сек/см2.
Согласно последнему уравнению, абсолютной единицей динамической вязкости называют вязкость такой жидкости, в которой сила в 1 дм перемещает находящиеся на расстоянииіслідруг от друга слои жидкости с поверхностью в 1 см2 каждый один относительно другого со скоростью 1 см/сек. Абсолютную единицу динамической вязкости называют пуазом.
В системе единиц СГС вязкость имеет размерность:
_ Їдн'секЛ Г г>см сек 1__________ Г г "]
Пуаз — L^-^a-J в J — [ см• сек J
Чаще всего в технической литературе вязкость приводится в единицах, равных 0,01 пуаза, т. е. в сантипуазах. В гидродинамике вязкость выражают в технических единицах, с размерностью кгс-сек/м2. Для того чтобы от абсолютной вязкости, выраженной в пуазах, перейти к вязкости в технических единицах, необходимо число пуазов разделить на 98,1, так как
1 кгс• сек/м2 = Qqq Дн• сек! см2 «= 98,1 дн-сек! см2 І
Величину, обратную вязкости—=т], называют текучестью.
Р
На практике вязкость жидкостей часто определяют в виде удельной вязкости, представляющей собой отношение вязкости данной жидкости (jj.) к вязкости воды при той же температуре:
J F-вод.
Отношение абсолютной вязкости к плотности жидкости называют кинематическим коэффициентом вязкости или просто к и н-е матической вязкостью:
V = М2/сек (1—186)
Р 7 V
Единицей кинематической вязкости является с т о"к с (cm), ["равный 1 смъ/сек или 100 сантистоксам (сст).
В лабораторной практике вязкость обычно определяют при помоши вискозиметров в градусах Энглера. Для жидкостей с ц>1 сантипуаза для перевода вязкости, выраженной в градусах Энглера, в вязкость, выраженную в технических единицах, пользуются формулой
У. = ^7,24Е— кгс-сек/м2 (1—18в)
Где Е—вязкость жидкости в градусах Энглера;
7—уд. вес жидкости в кгс/м3\ - ё—ускорение силы тяжести (9,81 м/сек2).
Вязкость можно рассматривать как функцию трения молекул друг о друга, зависящего от их строения и пространственного расположения. Поэтому изменение температуры жидкости существенно влияет на величину вязкости. Вязкость капельных жидкостей сильно уменьшается с повышением температуры и тем быстрее, чем выше величина вязкости; вязкость газов, наоборот, с возрастанием температуры увеличивается.
Для капельно-жидких тел зависимость вязкости от температуры не удается выразить одной общей формулой. Существует ряд эмпирических формул, найденных исследователями, применительно к большому числу жидкостей.
Вязкость органических жидкостей в зависимости от их строения и молекулярного веса можно вычислить по уравнению
Lg (lg н) = 1000 К - 2,9 (1-18г)
Где ц—вязкость жидкости при атмосферном давлении и 20°С в милли - пуазах (1 миллипуаз^0,001 пуаза); у—уд. вес жидкости в кгс/м3; М—молекулярный вес жидкости; К—константа, зависящая от строения вещества.
Числовое значение константы К находят по формуле
К = ЪАп + Ър (1—18д)
Где А—число одноименных атомов в молекуле соединения;
П—числовое значение атомной константы;
Р—поправки на группировку и характер связи (такое обозначение принято в таблицах).
Числовые значения пир находят в таблицах физико-химических величин[3].
Вязкость смеси взаимно-растворимых и неассоциированных жидкостей может быть найдена по уравнению
Ft*. (1—18е)
Или
Igf-cM. = Xglgfv (1—18ж)
\
Где fxlt [а2, —вязкость отдельных компонентов, составляющих смесь; х1г х2, х3—молярные концентрации (доли моля) отдельных компонентов в смеси.
Если для данной жидкости известна ее вязкость при двух каких - либо температурах, то вязкость этой жидкости при любой другой температуре может быть приближенно вычислена путем сравнения с вязкостью какой-либо аналогичной или «стандартной» жидкости, вязкость которой известна в широких пределах температур. Такой расчет производят, пользуясь условием линейности химико-технических функций, сформулированным в 1936 г. К. Ф. Павловым.
Основной предпосылкой этого условия является однозначность функций, т. е. строгое соответствие какому-то определенному значению функции только одной независимой переменной и, наоборот, строгое соответствие определенному значению независимой переменной только одного
значения функции. Примерами однозначных функций являются зависимости: давления паров чистых жидкостей от температуры р = f(t), вязкости от температуры ;х=ф(/) и др.
Пусть согласно понятию однозначности для какого-либо вещества
B = ср (а) и а = ф ф)
В таком случае для тех же параметров другого вещества Ьх = у(ах) и ах = ф (Ьх)\
Для одного и того же значения Ь, т. е. при b\=blt получим
Ср(а) = ср(а1) (А)
Разложив обе функции в ряды, можно легко установить прямолинейность уравнения (А); это позволяет при известных значениях в двух каких-либо точках и третьей контрольной, для любой зависимости сопоставляемых свойств двух веществ, графически представить функцию во всем ее диапазоне.
Исходя из условия однозначности химико-технических функций, можно графически и аналитически найти числовые значения вязкости любой жидкости из сопоставления вязкости данной жидкости с вязкостью воды, если только вязкость данной жидкости известна при каких - либо двух температурах.
Построим диаграмму (рис. 3), на которой по оси абсцисс отложена температура воды 6°С, а на правой оси ординат ее вязкость у. в пуазах. На левой оси ординат будем откладывать температуру t данной ^ идкости. Так как вязкость воды известна пр и разных температурах, нанесем на
Диаграмму кривую зависимости вязкости воды от температуры. Допустим, что для данной жидкости известны значения цж при при Ї. Вязкость воды будет равна p при температуре Ь и fj.' при температуре 6', чему на диаграмме соответствуют точки D и Е. А
Восстановив из точек D и Е перпендикуляры до пересечения с изотермами t и Ґ, найдем точки А и В. Эти точки, исходя из условия однозначности функций, должны лежать на одной прямой линии. Проведя через точки А и В прямую, получим линию, характеризующую вязкость данной жидкости в зависимости от температуры.
При помощи такой диаграммы можно найти вязкость данной жидкости для любой температуры в пределах диаграммы. Так, вязкость октана (линия АВ) при температуре 25° будет равна вязкости воды при температуре 55°—0,005 пуаз (точки М и N). Эту же задачу можно решить и аналитически, не прибегая к построению диа -
Т *SK АС
Граммы. 1ак, по рис. о для любых двух температур отношение =const
T — T'
Гг =const = К
Зная для двух известных точек числовое значение К, можно определить вязкость данной жидкости при заданной температуре t'. Вязкость жидкости будет
Равна вязкости воды при температуре 0', которую находят из уравнения
6'= 6 (1—18и)
Где t—температура данной жидкости, при которой вязкость ее равна'вязкости воды при температуре 6;
T'—заданная температура данной жидкости, при которой искомая вязкость ее будет равна вязкости воды при температуре О'
Вязкость суспензий в условиях, не выходящих за пределы гидравлического течения, определяется по формуле А. И. Бачинского
^ = +4,5ср) (1—18к)
Где [аж—вязкость чистой жидкости, являющейся дисперсионной средой суспензии;
Ср—содержание твердой фазы в суспензии, выраженное отношением объема твердой фазы к общему объему всей суспензии. Зависимость вязкости от температуры для газов и паров с достаточной степенью точности можно выразить формулой
273 + С I Т \|- /. . о V
Р/ = ^о "ТТС~(27з] (1 18л)
Где —вязкость газа при заданной температуре [х0—вязкость того же газа при 0°С; Т—температура газа, равная /°+273°; С—константа, зависящая от свойств газа (табл. 2).
Таблица 2
Значения константы С
|
Константа С Газ |
|
Газ |
Константа С
|
|
|
Закись азота..................... 312 Кислород........................ 110 Метан............................. 198 Окись азота.............................. 195 Окись углерода... 101 Сернистый ангидрид. 396 Хлор......................................... 351 |
Азот.......................
Аммиак...................
Бензол...................
Водород.... Водяной пар. . .
Воздух....................
|
1 | X*) | х3 |
Двуокись углерода
При повышении степени дисперсности твердых и жидких вешеств поверхность их значительно увеличивается и вместе с этим влияние поверхностных свойств соответственно возрастает. Увеличение поверхности тел требует затраты работы. Величину этой работы, отнесенной к единиг? поверхности, называют поверхностным натяжением и обозначают буквой с.
Если работу выразить в кгс-м, а плошадь псверхнссти слоя в м\ то поверхностное натяжение будет иметь размерность:
Кгс'М,
Ol = —= кгс/м 1 м
Работу можно выражать и в эргах, а плошадь поверхности в см2, в этом случае поверхностное натяжение будет иметь размерность:
Эрг ___ цдн>см __ дн
[см2 " см2 см
1 кгс/м Mm 9810 дн/см
Полученная размерность а показывает, что поверхностное натяжение можно рассматривать как силу, действукшую на единицу длины поверхности слоя.
Режим движения жидкосіи. При достаточно медленном движении жидкости в прямолинейном направлении пути отдельных ее частин представляют собой параллель нье прямые, сбра - .
Зуюшие на псЕорстах пра - | І грЩ|р|5р;
Бильную систему кривых. ъ \ Ё'яе>но*Р-
TOC \o "1-3" \h \z Таксе движение, ко - [ Ещі^і і—у I '
Гда частины жидкости у | ^іШШ^и
ДЕИЖуТСЯ Прямолинейно И '^c/t б * '
Параллельно друг другу, 7 п
В гидродинамике назы
Вается струйчатым Рис- 4■ Распределегие скоростей при ламинарном (/) v * и турбулентном (II) ДГІ'»"ЄГИИ жидкости в трубе.
Или л а м и н а р и ы м. J ;
Наоборот, при больших скоростях отдельные частины жидкости, даже в случае прямолинейного направления движения, будут двигаться беспорядочно, по запутанным кривым в различных направлениях, причем эти пути будут4 постоянно изменяться. Такое движение называется вихревым или турбулентным.
В случае ламинарного движения (рис. 4, /), когда отдельные частицы движутся параллельно друг другу по прямому трубопроводу, скорость оказывается наибольшей по оси трубопровода (кг0) и уменьшается к краям сначала медленно, а затем быстрее, пока не станет равной нулю у самой стенки. Распределение скоростей по дис метру трубопровода происходит по закону параболы; средняя скорость движении wcv_ равна половине максимальной.
При увеличении скорости упорядоченность движения нарушается и возникает турбулентное движение; скорость отдельных частиц становится непостоянной и колеблется как по величине, так и по направлению около некоторой средней величины. Средняя скорость параллельна оси трубопровода.
Распределение средних скоростей по диаметру d трубопровода в случае турбулентного движения выражается некоторой кривой, сходной с параболой, но только с более широкой вершиной (рис. 4, II). Вблизи
/ стенок остаётся пограничный слой а, где происходит примерно прямо - І линейное уменьшение скорости до нуля. В этом слое жидкость движется I ламинарно.
4 Таким образом, турбулентное движение не существует в чистом виде, а всегда сопровождается ламинарным.
Точно так же и при ламинарном движении имеется вихреобразова - ние, т. е. элементарные частицы жидкости, двигаясь поступательно,
Деформируются и вращаются, хотя их результирующая скорость направлена параллельно оси потока.
Описанное выше распределение скоростей по сечению трубы относится к гидродинамически стабилизированному движению, которое устанавливается на некотором расстоянии от входа жидкости в трубу. По опытам Никурад - зе для турбулентного движения это расстоянием—40d.
Кроме того, приведенные законы распределения скоростей верны лишь для изотермического движения жидкости, когда температура ее во всех точках потока одинакова и постоянна.
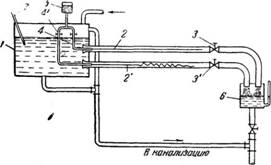
Рейнольде наглядно показал существование различных режимов движения жидкости следующим опытом (рис. 5). Из напорного бака 1 через круглую стеклянную трубу 2 выпускалась вода; количество протекающей вод зі регулировалось при помощи крана 3. Для того чтобы наблюдать характер движения жидкости, в трубу 2 через вставленную трубку 4 вводилась подкрашенная вода из бачка 5.
В определенных условиях струйка подкрашенной воды вытягивалась в трубе 2 в тонкую нить и двигалась, не смешиваясь с основной массой жидкости. Это показывало, что движение жидкости в трубе происходит параллельными несмешивающимися слоями (струйчатое или ламинарное). С уменьшением вязкости жидкости или увеличением ее скорости и диаметра трубы (труба 2') подкрашенная струйка размывалась и смешивалась с основной массой жидкости, т. е. ламинарное движение переходило в вихревое—турбулентное.
У— Режим движения жидкости может быть установлен по значению без - // размерной зависимости между скоростью движения жидкости w м/сек, / диаметром трубы с? ж, плотностью жидкости р кг-сек*/м* и ее вязкостью и кгс • сек/м2:
.M-s
Для случая движения жидкости по трубопроводам, на основании опытных данных Рейнольдса, уточненных впоследствии другими исследователями, можно принять, что при числовом значении безразмерной
|
Из водопровода |
|
Рис. 5. Определение режима движения жидкости опытным путем: /—напорный бак; 2, 2'—стеклянные трубы; 3, 3'— краны. 4, 4'—трубки; 5—бачок для подкрашенной воды; 6—сборник; 7—термометр. |
Величины (комплекса) меньшем 2320, устанавливается ламинарное движение, а при значении, большем 2320, устанавливается турбу - Ч.^.лентный режим движения.
Состояние движения, при котором ламинарный поток сменяется' турбулентным, называется критическим и значение комплекса (2320), соответствующее этому состоянию, также называется критическим.
Гтл ^ Wdp
|
КЄКр. Іг ZOZUfA. n ШкР. ■= —= ~-zr~ (1—19а) |
Таким образом, комплекс является основной величинои, определяющей вид движения вязкой жидкости, и поэтому он служит критерием движения реальной жидкости; для всех потоков, протекающих в подобных условиях, сохраняется постоянное его значение. Этот комплекс носит название критерия или числа Рейнольдса и соответственно обозначается
= Re (1-19)
Следовательно, критическое значение критерия Рейнольдса при движении жидкостей по прямым трубопроводам:
ReKP. = 2320
Из этого условия можно при данных значениях d, р и jx определить критическую скорость, соответствующую переходу от ламинарного движения к турбулентному:
ReKp. tu ___ 2320,u
Р D Р D
Следует, однако, иметь в виду, что критическое значение числа Рейнольдса зависит от ряда условий, в частности также от условий входа жидкости в трубу, от степени шероховатости стенок трубы и т. д. Поэтому при числах Re, близких к критическим, необходимо тщательно учитывать все условия, влияющие на режим движения жидкости.
Турбулентное движение становится вполне устойчивым только при Re^lO ООО. Прих2320</?е<10 ООО движение неустойчиво и оба вида движения могут проявляться совместно и легко переходить один в другой.
Гидравлический радиус. Диаметр труб и каналов нецилиндрического сечения выражают через. так называемый гидравлический радиус,- под которым понимают отношение площади свободного сечения трубопровода или канала, заполненного протекающей средой, к его смоченному пер ичм е т р у
Гг = 4т (1-20)
Где гг—гидравлический радиус в м\ /—площадь сечения в м2; П—смоченный периметр в м.
Для круглой трубы с внутренним диаметром d и, следовательно,
^ с itd2
Площадью свободного сеченияпри сплошном заполнении сечения жидкостью получаем значения: смоченный периметр
11 = Izd
Гидравлический радиус
7id2
F 4 D
Диаметр, выраженный через гидравлический радиус, называют эквивалентным диаметром:
D = d3 кв. = 4 гГ (1—20а)
Сопоставляя уравнения (1—20) и (1—20а), получим следующее общее выражение для эквивалентного диаметра:
4кв. — ТГ ж (1-206)
Для тррбы прямоугольного сечения со сторонами а и b гидравлический радиус равен
_ / ____ Ab _________ Ab
Гг ~ ТГ ~~ 2а - f 26 ~~ 2 (а + Ь)
И эквивалентный диаметр
І Л 4а£> 2Ab ., Nn Ч
Экв • = 4 гг - ^^ = JJ^ (1 20в)
Установившийся и неустановившийся поток. Поток любой жидкости, который движется достаточно долго по трубопроводу под действием не изменяющегося со временем давления, приходит в установившееся состояние. При этом в любом месте потока течение остается неизменно одним и тем же, т. е. все влияющие на движение величины не зависят от времени
£ =0
Ат
Де и—совокупность физических величин, влияющих на движение жидкости.
Такое движение жидкости называется установившимся или стационарным.
В отличие от стационарного, при неустановившемся движении величины, влияющие на движение, изменяются во времени. Так, например, скорость жидкости при неустановившемся движении будет меняться в зависимости от времени в каждой данной точке и при переходе из данной точки (xv yv zt) в любую другую (х2, у2, г2).
В этом случае скорость движения жидкости является функцией координат и времени:
W~f[(x, у, г, т) (1-21)
Примером неустановившегося движения является истечение жидкости из отверстия при переменном уровне ее в резервуаре.,В данном случае скорость истечения будет все время меняться в зависимости от изменения высоты напора, поэтому для скорости должен быть указан также и момент времени, которому она соответствовала.
Функциональная зависимость (1—21) показывает, что задание скорости движения временем, к которому она относится, а также геометрическими элементами, в пределах которых движется жидкость, полностью характеризует неустановившееся движение. Однако такая функциональная зависимость не выражает характера связи между величинами, определяющими неустановившееся движение.
Связь между этими величинами будет показана на основе теории подобия и теории размерности..
