Моделирование и исследование пусковых, остановочных, Циклических и других режимов работы машин и комплексов В технологическом процессе
Производим и продаем электроприводы ЭТУ, ЭПУ для двигателей постоянного тока, тел./email +38 050 4571330 / rashid@msd.com.ua
К типовым режимам управления электроприводами машин и комплексов относятся [8|: стабилизация, слежение, позиционирование, программное управление, синхронизация скоростей и положений, управление нагрузкой.
Разнообразие режимов работы электроприводов обусловлено различными режимами работы промышленных установок в технологическом процессе. Наиболее характерным является режим длительной работы электроприводов в установках с непрерывным технологическим процессом, т. е. непрерывных прокатных станах, бумагоделательных машинах, установках для производства полимерных материалов, кордных тканей и др. Как правило, такие промышленные установки являются многодвигательными и содержат от нескольких единиц до нескольких десятков электроприводов.
Режимы работы машин и комплексов могут быть кратковременными с программным управлением скоростью в широких пределах. Стабилизация скорости в таких случаях является частным режимом на небольших временных интервалах, что характерно для электроприводов ряда металлообрабатывающих станков и реверсивных прокатных станов.
При длительных непрерывных режимах работы машин и комплексов особых требований к режиму пуска электроприводов не предъявляется. Режим пуска здесь является вспомогательным, так как машины и комплексы проектируются исходя в основном из условий обеспечения заданной точности стабилизации скорости в установившемся режиме.
В современных системах управления электроприводами в качестве регуляторов используются модули КП.
При программной реализации регуляторов предусматривается анализ уровней заданных сигналов и ошибок систем, границ допустимых значений переменных, коррекция ограничений и другие дополнительные функции, обеспечивающие заданные или предельно достижимые динамические свойства систем.
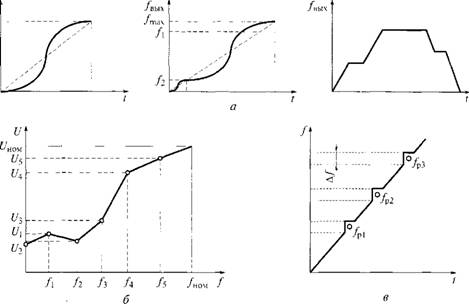
Позиционные режимы с прямоугольными временными диаграммами ускорений, обеспечивающие наибольшее быстродействие, неоптимальны по электропотреблению [7J и, самое главное, являются возбудителями полигармонических колебаний механизмов и источником дополнительных погрешностей движения исполнительных органов. Поэтому при обработке заданных перемещений используют алгоритмы формирования треугольных, трапеции-
дальных или гармонических временных диаграмм ускорений. При этом некоторая потеря быстродействия систем принципиального значения не имеет.
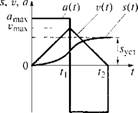
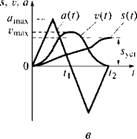
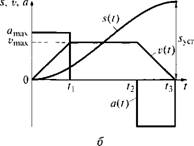
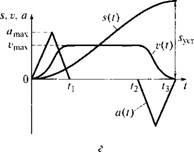
Применительно к линейным перемещениям на рис. 6.8, а, б показаны прямоугольные временные диаграммы ускорений a(t), а также диаграммы скоростей v(t) и перемещений s(t) для режимов малых и больших позиционирований механизмов, а на рис. 6.8, в, г — треугольные (при усилии сопротивления, равном 0).
Доминирующее применение частотно-регулируемых электроприводов с асинхронным короткозамкнутым двигателем при разработке технологического оборудования позволяет реализовывать их различные режимы работы. Преобразователь частоты совместно с модулями управления представляет собой интеллектуальный блок управления приводом, свойства которого довольно разнообразны.
Во многих преобразователях (Altivar ATV-66, FR-A500 и др.) предусмотрена возможность реализации законов управления с различными типами ускорения и торможения, например линейного (см. рис. 6.8, а, б) и S-образ- ного (рис. 6.9, а).
|
|
|
|
Например, S-образная характеристика Л (рис. 6.9, а) применяется при разгоне/торможении двигателей шпинделей станков, работающих обычно на номинальной скорости вращения (50 Гц и выше). В этом случае номинальная частота является конечной точкой кривой разгона. Приведенная S-образная характеристика В обеспечивает требуемый момент трогания и предотвращение
|
|
|
|
Риє. 6.8. Временные диаграммы ускорений a{t), скоростей v(t) и перемещения s(t):
А, б — прямоугольные соответственно для режимов малых и больших позиционирований механизмов; в, г — треугольные соответственно для режимов малых и больших позиционирований механизмов при усилии сопротивления, равном нулю
|
S-образная характеристика (А) ./пых Ушах |
|
|
|
S-образная характеристика (В) |
|
Компенсация люфта |
|
Нагрузка с постоянным моментом (конвейеры, станки) |
|
Ивых, % |
|
/ном /вых |
|
Ц. ЫХ. % 100 |
|
/ном /[(( |
Нагрузка с переменным моментом (насосы, вентиляторы)
|
Подъемник (стартовое напряжение: прямое вращение, реверсное)
Рис. 6.9. Законы управления с различными типами ускорения и торможения: |
|
Подъемник (стартовое напряжение: прямое вращение, реверсное)
|
А — S-образный; б — вида £///; в — функция, позволяющая вырезать из рабочего диапазона резонансные частоты; г — в зависимости от типа нагрузки
Повреждения грузов на конвейере, т. е. S-образное изменение частоты при переходе от текущего значения/, к заданному/2 определяет максимальную плавность хода.
Преобразователи частоты могут также реализовывать функцию компенсации люфта (см. рис. 6.9, а). Данная характеристика обеспечивает временную остановку изменения скорости при разгоне/торможении, что смягчает удар, возникающий при выборе люфта.
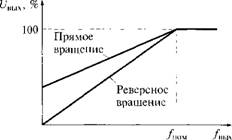
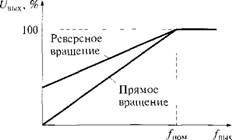
В приводах существует возможность формирования характеристики вида U/f с требуемыми стартовым и номинальным напряжениями (рис. 6.9, б) ив зависимости от типа нагрузки (рис. 6.9, г).
В некоторых случаях при управлении двигателем на отдельных частотах могут возникать резонансные колебания механической системы исполнительного механизма. Для избежания этих явлений в преобразователе существует функция позволяющая вырезать из рабочего диапазона резонансные частоты /рЬ /р2, /р3 (рис. 6.9, в).
Таким образом, формирование различных законов управления (требуемых входных воздействий) позволяет реализовывать различные режимы работы ЭП. При компьютерном моделировании с использованием MATLAB Simulink для этого можно применять как стандартные S-функции из разделов Sources (источники), Functions & Tables, Nonlinear, так и S-функции, разработанные пользователем. Стандартные S-функции из раздела Sources предназначены для описания рабочей нагрузки моделируемой системы, а также для формирования сигналов, обеспечивающих управление работой S-модели в целом или отдельных ее частей. Все блоки — источники сигналов имеют по одному выходу и не имеют входов (рис. 6.10).
В качестве источников сигналов (входных величин) могут использоваться следующие блоки:
Band-Limited White Noise (белый шум с ограниченной полосой) — генератор белого шума с ограниченной полосой;
Chirp Signal (гармонический сигнал) — источник гармонических колебаний переменной частоты;
Clock (часы) — генератор непрерывного временного сигнала;
Constant (константа) — источник постоянной величины (скаляра, вектора или матрицы);
Digital clock (цифровые часы) — источник дискретного временного сигнала;
Discrete Pulse Generator (дискретный импульсный генератор) — генератор дискретных импульсных сигналов;
Pulse Generator (импульсный генератор) — генератор импульсных сигналов;
Ramp (возбудитель) — генератор линейно возрастающего (убывающего) сигнала;
Random Number (случайное число) — источник дискретного сигнала, амплитуда которого является случайной величиной, распределенной по нормальному закону;
Repeating Sequence (периодический сигнал) — генератор периодического дискретного сигнала произвольной формы;
Signal Generator (генератор сигнала) — генератор непрерывного сигнала произвольной формы;
File Edit View Help
- Щ Simulink л
P - Commonly Used Blocks
Continuous ~h- Discontinuities ±-j Discrete
~h - Logic and Bit "Operations Lookup Tables Math Operations ІЗ- Model Verification ±i - Model-Wide Utilities ~h - Ports & Subsystems ~h - Signal Attributes b - Signal Routing
Sinks Ъ - Sources
|
[Ж |
|
EI |
User - Defined Funcbons + ~h- Additional Math & Discrete + fp| Aerospace Blockset + Щ CDMA Reference Blockset + Communications Blockset Щ Control System ТооІЬоч + Щг Embedded Target for Infineon C166fj + Щ Embedded Target for Motorolai. Ii HC1 + Щ Embedded Target for Motor olai. I.i MP1'.v
Band-Limited White Noise Chirp Signal
Constant
Counter Free-Running Counter Limited Digital Clock From File From V/uil space b round ilnl
Pulse Generator Flamp
Fiaridom Murriber Flepeating Sequence Flepeating Sequence Interpolated Repeating Sequence Stair Signal Builder Signal Generator S me Vv' d v'e Step
Uniform Random Number
Рис. 6.10. Раздел Sources MATLAB Simulink
Step (такт) — источник единичного дискретного сигнала с заданными параметрами;
Sine Wave (генератор гармонических колебаний);
Uniform Random Number (равномерное случайное число) — источник дискретного сигнала, амплитуда которого является равномерно распределенной случайной величиной.
Два блока из раздела Sources отличаются от перечисленных блоков тем, что обеспечивают использование в модели различных числовых данных, полученных ранее как с помощью Simulink, так и другими средствами MATLAB:
Блок From File (ввод из файла) обеспечивает ввод в S-модель данных, хранящихся в МАТ-файле;
Блок From Workspace (ввод из рабочей области) обеспечивает ввод в модель данных непосредственно из рабочей области MATLAB.
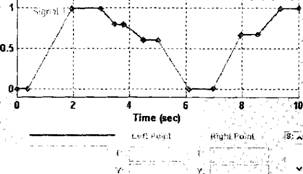
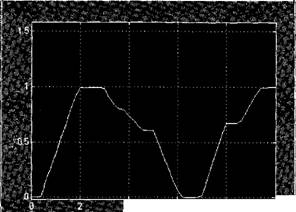
Структура данных в МАТ-файле представляет собой многомерный массив с переменным числом строк, которое определяется числом регистрируемых переменных. Элементы первой строки содержат последовательные значения модельного времени, элементы других строк — соответствующие значения переменных. Например, с помощью блока Signal Generator формируется сигнал, представленный на рис. 6.11.
В состав Functions & Tables входят три мощных и универсальных блока (рис. 6.12): Fen (функция), MATLAB Fen (функция MATLAB) и S-function (S-функция).
File Edit Group Siqnal Axes Help
|
U X ► |
Ц * Ъ Л 1' ~ ~ S A # M J
У Group 1
|
|
|
/Name: SignaM Index: 1 j-j |
|
Pick to select point or segment Shift+cficte to add points |
|
І Signal |
A
Figures - Scope
|
J File Edit Debug Desktop Window Help * * x |
|
Mmmmm. |
|
тш-р pm л a в eif ІШВ9П |
Рис. 6.11. Блок Signal Generator MATLAB Simulink:
A — сформированная диаграмма изменения скорости привода; б — модель изменения скорости привода
File Edit View Help
- ЛІ Simulink
ІН Commonly Used Blocks Continuous Discontinuities ;Ы Discrete
I^j Logic and Bit Operations i> Lookup Tables i> Math Operations Model Verification ;Ы Model-Wide Utilities :Ы Ports Et Subsystems i> Signal Attributes І5-: Signal Routing ly Sinks i>! Sources
Embedded MATLAB Function
M-file |level-2) S - Function MATLAB Fen S-Function Function Builder Function Examples
Рис. 6.12. Состав S-Functions MATLAB Simulink
В качестве параметра настройки блока Fen можно ввести любое вычисляемое выражение, аргументом которого является значение входного сигнала. В качестве операндов вычисляемого выражения блока Fen могут также использоваться переменные, находящиеся в рабочей области MATLAB.
Блок MATLAB Fen позволяет применить к входному сигналу любую процедуру обработки, реализованную в виде М-файла. Это может быть как библиотечная функция пакета MATLAB, так и подпрограмма, созданная разработчиком S-модели.
Блок S-function обеспечивает использование в блок-диаграмме так называемых S-функций. Такая функция является самостоятельной программой, написанной на языке MATLAB или C/C++, которая имеет определенную структуру и хранится в М-файле или в МЕХ-файле.
Стандартными аргументами S-функции являются:
Т — вектор значений модельного времени;
X — множество состояний моделируемой системы (непрерывное или дискретное);
U — вектор входных воздействий;
FLAG — признак, определяющий формат представления результата [61].
S-функция может также иметь произвольное число дополнительных аргументов, назначение которых определяется разработчиком. Примеры S-функций, реализованных в виде М-файлов и хранящихся в папке matlabtoolbox simulinkblocks, могут быть использованы в качестве шаблонов для создания собственных S-функций.
В качестве примера рассмотрим S-функцию, реализующую график движения кабины лифта [8]. Исходными данными для рассчета являются: vycT — установившееся скорость движения лифта; а — ускорение; р — рывок.
S-функция lift:
Function (sys, хО, str, ts] = lift(t, x,u, flag, vust, a, ro)
-з
% Шаблон для создания S-функции — файл sfuntmpl. m
Switch flag, % В зависимости от значения переменной flag происходит % обращение к той или иной процедуры ответного вызова:
% Инициализация
Case О
[sys, хО, str, ts] = mdl Init iali zeS і zes (vust, a, ro);
® Вычисление вектора выходных сигналов
Case З
Sys = mdlOutputs(t, х, u, vust, a, ro);
% Неиспользуемые значения переменной flag
% В примере не используется процедура завершения S-функции, нет % непрерывных и дискретных переменных состояния, поэтому значения % переменной flag = 1, 2, 4, 9 не задействованы.
% Результатом работы S-функции в этих случаях является пустой массив.
~б
Case { 1, 2, 4, 9 } sys = [ ];
% Неизвестное значение-переменной flag
Otherwise
Error ([' Unhandled flag = ', num2str(flag)]); end
% Конец функции lift
-б
% mdlInitializesіzes % mdlInitializesіzes % Функция инициализации
% Расчет начальных условий, тактов дискретности, размеров векторов сигналов,
% массива тактов и задержек
О.
Function [ sys, хО, str, ts] = mdllnitializeSizes(vust, a, ro)
Sizes = simsizes; sizes. NumContStates = 10; sizes. NumDiscStates = 0; sizes. NumOutputs = 7;
Sizes. Numlnputs = 3;
Sizes. DirFeeathrough = 1;
Sizes. NumSampleTimes = 1;
Sys = simsizes(sizes) ;
Число непрерывных переменных состояния Число дискретных переменных состояния Число выходных переменных Задается динамически. Число входных переменных Задается динамически.
Прямая передача входного сигнала на выход.
Размер вектора тактов квантования.
Str = [ ] ; хО = [ ] ; ts = [0 Ob-
Sizes = simsizes; % Конец процедуры mdllnitializeSizes % mdlOutputs
% Функция вычисления вектора выходных сигнал:в
Function sys = mdlOutputs(t, х, u, vust, a, rc)
X(1) = a*a/(2*ro);
X (2) = vust — a*a/ (ro) ;
X (3) = a *a/(2 * ro) ;
X(4) = vust;
X(5) = - a*a/(2*ro);
X (6) = — vust + a*a/(ro);
X(7) = - a*a/(2*ro) ;
Sys = x;
End
% Конец процедуры mdlOutputs
|
» Параметр заразервирован для будущего % использования. ^ Задание вектора начальных значений % переменных состояния. % Такт квантования и задержка. % Такт наследуется от предшествующего блока. |
Для моделирования ограничений на выходные сигналы регуляторов и технологические параметры можно применить раздел MATLAB Simulink Nonlinear (рис. 6.13).
Сочетания приведенных ранее разделов MATLAB Simulink позволяют реализовывать различные режимы работы ЭП.
Sim ulinkLibraryB rowse г
File Edit View Help
Ъ-' Discontinuities
Discrete Ъ - Logic and Bit Operations |>i Lookup Tables
Math Operations Ъ-'. Model Verification
Model-Wide Utilities ІН Ports & Subsystems
|
Coulomb & Viscous Friction Dead Zone І И^ j Dead Zone Dynamic |
|
M |
|
Hit Crossing Quantizer Rate limiter ) 1 Rate Limiter Dynamic Relay Saturation Saturation Dynamic Wrap To Zero |
Signal Attributes ІЗ-; Signal Routing 5inks Sources br User-Defined Functions
Рис. 6.13. Раздел MATLAB Simulink Nonlinear, библиотека Discontinuities
В качестве примера рассмотрим компьютерное исследование системы управления ножницами с катящимся резом. Описание автоматизированных электроприводов и системы управления см. в [8].
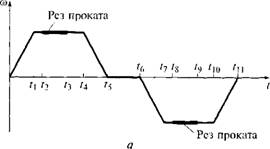
Выбором параметров кинематической схемы ножниц и профиля ножа обеспечиваются требуемые условия реза листа при качении ножа относительно проката при минимальном угле реза. Исключение скольжения ножа относительно металла обеспечивает минимизацию затрат энергии при резе. Система управления в соответствии с заданием реализует циклические движения ножниц при резе в прямом и обратном направлениях. Временные диаграммы изменений скорости со, угла а. и момента М кривошипа при прямом и обратном резе показаны на рис. 6.14. На участках 0.../,, ?4...?5, t6...t1, tm...tn изменение угла происходит по параболе.
|
|
|
|
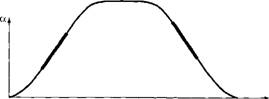
Для обеспечения плавности разгона и торможения целесообразно использовать S-образную характеристику изменения скорости (рис. 6.15), входящую в меню параметрических настроек приводов Simovert. График изменения
|
|
Рез проката
Рис. 6.15. Временная диаграмма изменения скорости с S-образными характеристиками разгона и торможения
Ускорения в режимах разгона и торможения в этом случае имеет вид треугольника (в отличие от прямоугольного графика изменение линейной скорости).
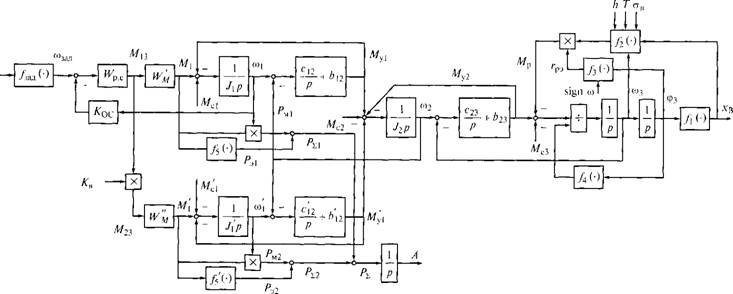
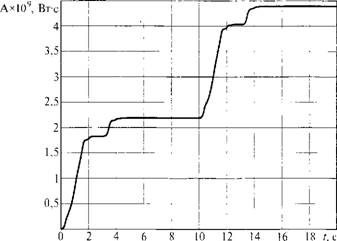
Математическая модель системы управления движением однокривошип - ных ножниц показана на рис. 6.16. Модель отражает динамические процессы в системе управления с учетом упругих деформаций в механической части электропривода и выравнивания нагрузки электродвигателей. Так как кроме исследования динамических характеристик системы необходимо выполнить оценку энергозатрат на цикле реза, структурная схема дополнена элементами оценки энергии А в интервале времени цикла 7^. Все параметры и переменные системы управления приведены к валу кривошипа.
На схеме обозначены:
WM, W"M, Wpc — передаточные функции соответственно замкнутых контуров регулирования моментов Mh М2 и регулятора скорости;
Кв — коэффициент выравнивания нагрузки двигателей (при Кп= 1 двигатели имеют по половине номинальной нагрузки кривошипа);
^ос — коэффициент обратной связи по скорости (Кос = АдС/р (где Кж — коэффициент датчика скорости, /р — передаточное число редуктора);
/тад(') — функция задания управляющего воздействия созал;
Fs(')i fs(') — функции, определяющие электрические потери в приводе;
Мц, М2І — сигналы задания моментов электродвигателей;
А/с1, M'cU Д/с2, Мс3 — моменты сопротивлений в элементах привода, обусловленные силами трения;
^эь Рп, Pa, Pz — мгновенные мощности соответственно механические, электрические и суммарные;
А — энергия на цикле реза.
Регулятор скорости и замкнутые контуры регулирования моментов являются частью комплектных электроприводов Simovert VC. Следует параметри - ровать регулятор скорости как ПИ-регулятор.
Для моделирования используется ПИ-регулятор скорости с следующими параметрами передаточной функции:
|
|
UJ
Ю
|
Рис. 6.16. Математическая модель системы управления движением однокривошипных ножниц |
Ррс=_______ ^Р______ ; Трс= —,
Р'С AT^d/У, )ЛГос ' pt соср
Где соср — частота среза, определяемая в соответствии с минимальной частотой упругих колебаний привода; Км — передаточный коэффициент замкнутого контура регулирования момента.
Для двигателя, имеющего />ном = 400 кВт, яном = 1000 об/мин, Мнт, = 3826 Н м, Мтах = 8800 Н м, и редуктора с /р = 117,2 получим: Км = 1,03 х 105 Нм/В; J, ~ = 313 103 кг м2; Кос = 11,7 В/рад/с; cowllill = 160 1/с; соср = 20 1/с; трс = 0,1 с; Рр. с = 5,19.
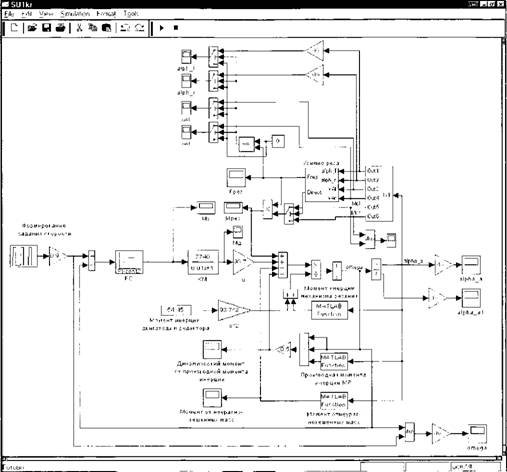
Компьютерная модель системы управления, реализованная в Simulink MATLAB в соответствии с математическим описанием, приведенным на рис. 6.16, показана на рис. 6.17.
Функциональные зависимости /j(-) ...fs(-) вводились отдельными программами, написанными в среде MATLAB. Модель может быть расширена, если
|
Рис. 6.17. Компьютерная модель системы управления, реализованная в MATLAB Simulink в соответствии с математической моделью, показанной на рис. 6.16 |
Необходимо выполнить исследование динамических нагрузок (упругих момен тов) любых выбранных элементов механической части электропривода. С ис пользованием разработанной модели можно исследовать:
П, об/мин 10
8
6
4
2
0 -2
|
Рис. 6.19. Переходный процесс по углу резания |
|
О-а, ° 350 300 250 200 150 |
|
Рис. 6.21. Переходный процесс энергии, затрачиваемой на резание заданные диаграммы движений ножниц; Динамические нагрузки, возникающие в суммирующей шестерне редуктора при отличии друг от друга динамических характеристиках замкнутых контуров регулирования моментов двух приводов; Динамические процессы в системе и ножницах при воспроизводстве заданных движений; Энергетические характеристики привода в виде изменений отдельных составляющих мощности, суммарной мощности и энергии в процессе реза листового проката разного сортамента; Кинематику, динамику и энергию ножниц, задав произвольного вида функциональные зависимости /і(-) •••/((•)• Результаты исследования динамических характеристик представлены на рис. 6.18...6.20, а энергетических — на рис. 6.21. |