Строительные машины и оборудование
Конструктивный расчет вибрационных грохотов
Расчет включает определение параметров деталей вибропривода (дебалансов, подшипников, вала), опорных амортизационных устройств (пружин), мощности электродвигателя привода,,а также массы опорного основания, исходя из условий виброизоляции рабочих мест обслуживающего персонала.
Работа виброгрохотов происходит, как правило, в зарезонанс - ном режиме, при частоте вынужденных колебаний f, значительно превышающих частоту собственных колебаний fo(f^>fo)-
У грохотов с круговыми колебаниями при вращении дебалансов возникают центробежные силы, сумма которых составит вынуждающую силу вибратора (Н):
Fa—mR(e—а)/2,
Где тя — суммарная масса установленных на грохоте дебалансов, кг; е — эксцентриситет дебалансов, м; а — амплитуда колебаний короба грохота, м; f — частота вынужденных колебаний, Гц.
Величина вынуждающей силы является определяющей при расчете вала вибратора, подшипников. Расчетная схема вала приведена на рис. 8.15. На один конец вала действует сила Fn/2, на второй — сумма сил Ря/2 и окружного усилия Р клиноременной передачи. Расчет вала производится по методике, изложенной в курсах деталей машин. При расчете подшипников на долговечность по общепринятой методике следует иметь в виду, что возмущающая сила является циркулирующей по отношению к наружному кольцу подшипника и неподвижной по отношению к внутреннему кольцу. Это обстоятельство должно учитываться соответствующим коэффициентом и посадками колец подшипника.
Расчет дебалансов (определение их размеров) производится с учетом инерционных сил, возникающих при круговом движении короба грохота с материалом вокруг точки С (центр масс грохота) (рис. 8.16). Инерционная сийа (Н) равна Л, о=«ва/2, где 98
Тв — вибрируемая масса, кг; mB=mK+K/rmM, кг; тм —масса короба грохота с закрепленными в нем ситами; тк —масса материала, находящегося на ситах грохота; К'—Ь,15... 0,2 — коэффициент присоединения сортируемого материала. Пренебрегая силами сопротивления упругих опор короба грохота (Pci), как предельно малыми по сравнению с FR, рассматриваемые силы (/•'д и Ріа) в каждый момент времени будут равны, что и обеспечивает неподвижность точки С:тл—(е—a)f2 = mBaf2. Преобразуя выражение, получим mnef2= {mA+mB)af2. Поскольку масса деба - лансов тд обычно мала по сравнению с массой короба грохота и находящимся в нем материалом, в дальнейших расчетах при рассмотрении инерционной силы ею пренебрегаем. Тогда mnef2 = = mBaf2 или тле—тва.
Левая часть уравнения представляет собой суммарный статический момент установленных на валу дебалансов, равный n>SA, а правая часть — кинетический момент виброгрохота К, т. е.
NSx=K, (8.9)
Где п — число дебалансов вибратора; SR — статический момент одного дебаланса. Следовательно, кинетический момент виброгрохота равен сумме статических моментов дебалансов.
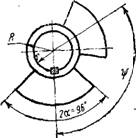
Статический момент одного дебаланса (Н-м) 5д=Сва/га. По найденному значению определяют геометрические размеры дебаланса. Обычно из условия, что дебаланс должен обладать наибольшим статическим моментом при минимальном моменте инерции, его изготовляют в виде сектора с центральным углом (рис. 8.17), равным 96°. При такой геометрии дебаланса его статический момент определится из следующей зависимости: S^=2/3(R3—r3)8p sin ф/2, где
6 —толщина дебаланса; р —плотность рис. g.17. Дебалансы материала. Обычно задаются величина - вибратора
|
|
|
Рис. 8.16. Схема к расчету де- балансов грохота с круговыми колебаниями |
|
Рис. 8.15. Схема к расчету вала вибратора грохота с круговыми колебаниями |
7* 99
ми і? и г и определяют значение толщины (м):
2 (.Ra-^-r») Р sin у/2)'
В связи с необходимостью изменения амплитуды колебаний при сортировке смесей различной крупности конструкции дебалансов должны допускать легкую регулировку статического момента. Наиболее целесообразной конструкцией дебаланса можно считать сдвоенный дебаланс (рис. 8.17,6), состоящий из двух самостоятельных дебалансов. Один из них неподвижно закреплен на валу, а второй может проворачиваться и фиксироваться в нужном положении. В зависимости от угла поворота - ф подвижного дебаланса изменяется результирующий статический момент,
Который равен 5дСум=^-(/?3—r3)6sin-|- cosр. При - ф=0 возникает наибольший статический момент," который определится из условия, что значение динамического коэффициента режима работы грохота будет принято по верхнему пределу, а частота вращения вала вибратора — по нижнему.
Расчет пружинных амортизаторов сводится к определению жесткости опорных конструкций и рабочих мест обслуживающего персонала. Для этого необходимо, чтобы сила, передаваемая через опорные пружины, была малой величиной. При установке в качестве амортизаторов винтовых пружин их упругая сила будет пропорциональна амплитуде колебаний (Н): Pc, a=c„a, где Сд —Общая жесткость опорных пружин грохота, Н/м.
C„=mBf о2, (8.10)
Где f0 — частота собственных колебаний грохота на опорных пружинах (Гц). Из выражения (8.110) следует, что жесткость опорных пружин может изменяться только за счет собственной частоты колебаний, так как вибрируемая масса (тв) определяется размером грохота. Следовательно, для обеспечения малой величины жесткости опорных пружин необходимо иметь малую fo.
Исследованиями установлено, что значение fo/f должно назначаться с учетом вынужденной частоты собственных - колебаний. При /=14 ... 20 Гц отношение fo/f должно находиться в пределах f0/f=l/4 ... 1/6 или fo=(l/4 ... l/6)f. Тогда жесткость опорных пружин (Н/м) Сд=тд(1/16 ... 1/36)f2 и соответственно упругая сила опорных пружин, передаваемая на опорные конструкции (Н), Рс, а=( 1/16 ... 1/36) mBaf2. Полученное выражение можно записать в следующем виде: Pc, a=fo2FB/f2, где /о2//2 — коэффициент передачи упругой силы через опорные пружины на основание (фундамент). Зная величины Рс, а и — силу тяжести фундамента с учетом неподвижной рамы грохота, можно определить величину амплитуды колебаний, передаваемых на основание (фундамент). Взаимосвязь упругой силы (Рс, а) с кинетическим 100
Моментом Кф будет равна Pc, a=K$t2/g, откуда K^~Pc, agf!2. Кинетический момент
Кф^вфОс ан, ' (8J11)
Где оф — сила тяжести фундамента с учетом неподвижной рамы грохота, аСаи — амплитуда колебаний, допускаемая санитарными нормами, м.
Мощность двигателя (кВт) привода виброгрохота расходуется на колебания короба грохота с материалом и на преодоление сопротивлений в подшипниках грохота, т. е.
ЛГДВ= {Nt+N^/n ПР> (8.12)
Где тіпр — кпд привода.
Первая составляющая мощности (Nі) представляет собой работу вынуждающей силы Рд, совершаемой в единицу времени, т. е. Ni—Fnaco/1000, где ш —угловая скорость, рад/с. Мощность, расходуемая на преодоление сопротивлений в подшипниках, #2= =МтрСо/1000, где Мтр=РдцО/2, Н-м; р, — приведенный коэффициент трения для подшипников качения (р,=0,005 ... 0,001); D — диаметр вала, м; со — угловая скорость, рад/с. В инженерной - практике для определения мощности приводного электродвигателя пользуются экспериментально найденной удельной энергоемкостью AN= (0,015 ... 0,02) Вт/(Н-м), т. е. затратой мощности на единицу кинетического момента виброгрохота. Тогда
N=AlN Ктах/1000. (8.13)
|
(Н) Pitt=—mjc, где х — (виброускорение), х = |
|
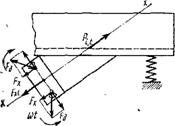
Рис. 8.18. Схема к расчету грохота с направленными колебаниями |
У грохотов с направленными колебаниями (рис. 8.18) синхронно-синфазное вращение дебалансов создает вынуждающую силу Fx, t, равную сумме составляющих центробежных сил дебалансов (Н) в направлении оси колебаний (Fx) : Ft, x=nFncosat, где п — число дебалансов двухвального вибратора. Под действием вынуждающей силы в колеблющейся системе (короб грохота с материалом) возникает сила инерции ускорение колеблющихся частей = (a cos Ш) =— асо2 cos со^. Следовательно Р4,г=твасо2 cos со£. Пренебрегая упруговязкими силами сопротивления опор и рабочего органа, как весьма малой величиной по сравнению с вынуждающей силой, запишем условие равновесия колеблющейся системы: nFbCos coЈ + mBaco2 cosco/=0 или по амплитудному значению + + mBa<a2=0. Отсюда Fa>x=—mBaco2, где знак «—» означает, что принятое направление силы Ft, x (см. рис. 8.18) будет обратным, так как колебательная система работает на мягких опо-
pax в зарезонансной области, когда вынужденные колебания совершаются в противофазе с вынуждающей силой.
Методика расчета остальных параметров виброгрохота с направленными колебаниями аналогична приведенной выше при расчете виброгрохотов с круговыми колебаниями, кроме расчетной схемы нагружения вала вибратора. Для обеспечения синхронно-синфазной работы обоих вибровалов обычно применяется зубчатая пара в закрытом исполнении, и на вал будут действовать следующие силы: вынуждающая Fa, радиальное усилие зубчатой передачи Fz и окружное усилие клиноременной передачи Р.