КОТЕЛЬНЫЕ УСТАНОВКИ И ПАРОГЕНЕРАТОРЫ
Свободная энергия Гиббса
Из курса термодинамики известны такие параметры системы, как давление р, температура t (Т), объем V, внутренняя энергия £/, эйтальпия Я, энтропия S и т. д.
Чистое вещество обладает основным термодинамическим свойством — свободной энергией.
Свободная энергия зависит от:
— химической природы вещества;
— количества вещества в образце;
— фазового состояния вещества (твердое, жидкое, газ);
— температуры;
— давления.
В зависимости от условий совершения работы над объектом используют два подхода к расчету свободной энергии вещества:
А) при постоянном давлении и температуре рассчитывают свободную энергию Гиббса, кДж/кг,
G — Н - Т5;
Б) при постоянном давлении и объеме системы — свободную энергию Гельмгольца, кДж/кг,
F = U — TS.
В дальнейшем будем рассматривать, в основном, свободную энергию Гиббса.
Рассмотрим значения параметров в точке Т = О К, р — 0:
А) С?(0) — Я(0); F(0) — U(0); в этой точке свободная энергия Гиббса равна энтальпии, а свободная энергия Гельмгольца — внутренней энергии системы.
Б) Учитывая, что H—U+pV, в нулевой точке Н(0) — 17(0), т. е. энтальпия и внутренняя энергия равны. Это приводит к равенству G(0) = F{ 0).
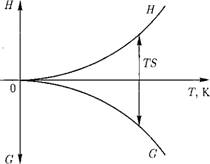
Как изменяются энтальпия и свободная энергия Гиббса при увеличении температуры системы при постоянном давлении (р Ф 0)?
В точке Т = OK G{0) = = #(0) примем G(0) - Я(0) - 0 (рис. 12.5).
|
Рис. 12.5. Зависимость энтальпии Н и свободной энергии Гиббса G от температуры Т. |
При подводе теплоты Q к системе увеличиваются ее энтальпия и температура. Мерой изменения энтальпии системы является теплоемкость Ср,
КДж/(кг-К),
|
|
При Т > О К ср > О; Т О К ср О.
С ростом температуры изменяется структура вещества, возрастают подвижность молекул, хаотичность их движения, т. е. увеличивается энтропия системы S.
Энтропия является мерой изменения свободной энергии
DG _ с df-~b-
При Т > OK S > 0; при T-+0KS-+0.
С увеличением температуры и энтропии системы свободная энергия Гиббса (аналогично — свободная энергия Гельмгольца) уменьшается (рис. 12.5).
Таким образом, изменение свободной энергии связано с изменением структуры системы, с хаотичностью движения молекул вещества.
|
При увеличении температуры Т. бодной энергии Гиббса G при увеличе Нии температуры Т. |
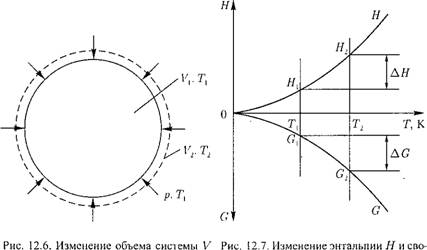
Возьмем систему объемом Vi с температурой Т (рис. 12.6), находящуюся под внешним давлением р. Этим условиям отвечают значения энтальпии #1, свободной энергии G1 (рис. 12.7). Окружающая среда имеет также температуру Т[.
Подведем к системе теплоту в количестве Q. Энтальпия изменится на величину
М'
Где М — масса системы.
Температура системы увеличится на величину
АТ = —
Где Ср — средняя теплоемкость в данном интервале температуры.
Новое значение температуры Т2 будет равно
Т2 = Ті + AT.
Свободная энергия Гиббса примет новое значение G2 (рис. 12.7). Изменение свободной энергии AG будет составлять
AG = Gi-G2> 0.
Следовательно, при подводе теплоты к системе (совершения работы над ней) изменение свободной энергии Гиббса положительно, т. е. AG > 0.
Какое соотношение между АН и AG?
При увеличении температуры Системы увеличивается ее объем до V2 (р = const), на что расходуется часть подводимой энергии в количестве pAV, где AV = V2 — V. Для совершения работы остается АН —pAV, что соответствует изменению свободной энергии Гиббса
AG = AH-pAV.
Изменение свободной энергии измеряется максимально возможной полезной работой, совершаемой в ходе процесса.
При подводе теплоты к системе полученная температура Т2 выше первоначальной Ті, соответствующей температуре среды, окружающей выделенную систему. «Отпустим» систему, при этом будет происходить самопроизвольное снижение ее температуры до температуры окружающей среды Ті, т. е. система будет самопроизвольно восстанавливаться в первоначальное состояние. Изменение свободной энергии при этом будет иметь отрицательное значение
AG = G2 - Gі < 0.
В процессе, протекающем самопроизвольно, изменение свободной энергии Гиббса отрицательно AG < 0.
При равновесии системы с окружающей средой изменение свободной энергии Гиббса равно нулю (ДО = 0).
Свободная энергия Гиббса измеряется в кДж/кг. Часто используют мольную величину свободной энергии Гиббса д, кДж/моль,
Д — h — Ts,
Где /і, s — мольные значения энтальпии и энтропии, соответственно, кДж/моль, кДж/(моль-К). Соотношение д — G/n.
Число молей п в килограмме вещества определяется через молекулярный вес т, г/моль,
П= 1000
П т •
Для воды (Н2О) т — 18 г/моль, число молей в 1 кг п = =55,5(5).
12.2.2. Понятие о химическом потенциале
Рассмотрим однокомпонентную систему (состоящую из одного чистого вещества).
Полезная максимальная работа, совершаемая в ходе процесса в одно - компонентной системе, определяется изменением свободной энергии Гиббса dG.
Свободная энергия Гиббса
G — Н — TS. (12.6)
Полный дифференциал этой величины
DG = dH - Td, S - SdT. (12.7)
Так как Я = U + pV, то
DH = dU +pdV + Vdp. (12.8)
По 1 и 2 законам термодинамики изменение свободной энергии dU выражается следующим образом:
DU = TdS-pdV. • (12.9)
DG = Vdp-SdT.
При равновесии системы dG = 0, для этого должны выполняться условия dp = 0, dT = 0, т. е. р = const, Т = const.
Возьмем многокомпонентную систему, например, раствор примесей в воде. Объем системы V (рис. 12.8). Компоненты і = 1 - N масса г-й компоненты М*; молекулярный вес ти число молей щ = Mi/rrii. Масса всей системы
N
Общее число молей
N
П
Мольная доля г-й компоненты
В многокомпонентной системе величина свободной энергии Гиббса зависит не только от давления и температуры, но и ее состава. Работа расширения и изменения состава системы будет определяться полным дифференциалом свободной энергии Гиббса
DG=(6-f) - dp+Ш) .dT + jr(M-) - dMi. (12.11)
�р J TMi оТ J рМ, j v 0 ЛІ г J p, T, A'J — M,
Индекс M — Мі означает постоянство массы всех компонент, кроме г-й. Сопоставление (12.10) с (12.11) показывает, что
(¥) =У-< (і)
др /ТМ, Ы / р, М;
|
(12.10) |
|
Рис. 12.8. Схема многокомпонентной системы объемом V. |
|
Из (12.6)—(12.9) получаем, что |
В чем смысл третьего члена выражения (12.11)?
Введем обозначение
Иг = (щ-) ■ (12.12)
Величину рг называют химическим потенциалом. Какими свойствами обладает величина
1. Самопроизвольное перемещение части массы г-го компонента из точки 1 в точку 2 возможно, если Ф т. е. если имеется неоднородное, поле потенциалов pi.
2. Перемещение массы dMi происходит в сторону убывания щ.
3. Равенство = р^ выражает условие равновесия, при котором самопроизвольного перемещения массы не существует.
Таким образом, химический потенциал г-ой компоненты показывает изменение свободной энергии Гиббса г-ой компоненты при изменении ее массы, когда давление, температура системы и масса остальных компонент остаются постоянными.
Полный дифференциал свободной энергии Гиббса для многокомпонентной системы будет иметь вид
N
DG = Vdp-SdT + Y^VidMi. (12.13)
2=1
Условия равновесия системы (dG = 0):
Dp = 0; dT = 0; ±і = const; dMi = 0; т. е. p = const; T = co;ist; pi — const; Mi = const.