КОТЕЛЬНЫЕ УСТАНОВКИ И ПАРОГЕНЕРАТОРЫ
Виды движения жидкости
При движении однофазного потока в трубе жидкая (или паровая) фаза заполняет все сечение трубы неразрывно, ограничивающей поток поверхностью является стенка трубы, свободная поверхность отсутствует. Скорость потока при обогреве изменяется по радиусу и длине трубы, средняя скорость в любом сечении положительна (по направлению потока). В двухфазном потоке, в общем случае от х — 0 до х = 1, при установившемся движении скорости жидкости и паровой фаз положительны, обе направлены по ходу среды, количество и распределение их по сечению характеризуются Расходными и истинными параметрами течения. Отсутствует свободная по - ВеРхность, ограничивающая поток сверху (или снизу). Движение жидкости, при котором она заполняет все сечение трубы, скорости фаз отличны от
нуля и поток по направлению течения не ограничен свободной поверхностью, называется напорным. При напорном движении относительная скорость w0Tн = w* - wl может быть положительной или отрицательной. Какой режим движения будет, если скорость воды или пара будет равна нулю?
|
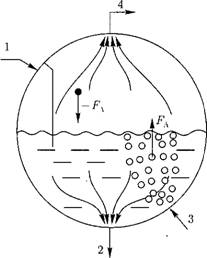
Рис. 8.14. Схема потоков воды и пара в барабане котла: 1 — вода из экономайзера; 2 — вода в опускные трубы; 3 — пароводяная смесь из подъемных труб; 4 — насыщенный пар в пароперегреватель. |
Рассмотрим схему потоков воды и пара в барабане парового котла (рис. 8.14). Нижнюю половину барабана занимает жидкая фаза (вода), верхнюю — пар. Жидкая фаза имеет сверху свободную поверхность. Часть воды непрерывно подается в опускные трубы контура циркуляции, а пар удаляется в пароперегреватель. Скорости движения воды и пара в барабане относительно невелики. Из подъемных труб в барабан поступает пароводяная смесь. На паровые пузырьки, попадающие в относительно неподвижную жидкую фазу, действует сила Архимеда, и они всплывают вверх. Это явление называется барботажем пара через воду. С другой стороны, на каплю воды, попадающей в паровой объем барабана, также действует сила Архимеда, но так как плотность капли (воды) больше плотности окружающего ее пара, сила Архимеда направлена вниз. При малой скорости пара капля воды будет падать в водяной объем. Процесс отделения воды от насыщенного пара называется сепарацией пара. Барботаж пара и сепарация пара имеют общие закономерности. Движение одной фазы потока в неподвижном или медленно движущемся слое второй фазы, при котором сверху имеется свободная поверхность, разделяющая фазы, называется безнапорным движением двухфазной среды. Определяющей силой в безнапорном движении является сила Архимеда.
Напорное движение создается разностью давлений в различных поперечных сечениях потока. Перепад давления между этими сечениями Ар определяется сопротивлением трения, местным сопротивлением, сопротивлением ускорения и нивелирным сопротивлением:
Ар = Дрф + Дрм + Друек + Ар,
|
Насос Л ~ Л |
-ф- 9 АР|' ? АР2 * 9 рх flip, I ^ ^
Насос р р
|
Я |
|
Н |
|
Я, |
|
Я> "а Р> |
|
_ АР* в) |
|
ДР2 |
|
АР, |
|
2Т |
|
Б) |
Рис. 8.15. Схемы принудительного движения (я, б) и естественной циркуляции (в).
Возьмем два участка, включенных последовательно по схемам а и б рис. 8.15. Давление среды в сечениях 1, 2 и 3 равно, соответственно, рь P2 и р3. Перепад давления на участках Арі = pi - р2, Др2 = Р2 - Рз, суммарный перепад давления Ар = Арі - f Др2 — Pi — Рз - Для преодоления сопротивления насос должен создать напор, равный Ар; следовательно, движение потока по учаеткам 1 и 2 происходит под воздействием сил давления, развиваемых насосом. Такое движение потока называется принудительным.
Соединим сечения 1 и 3 участков 1 и 2 (схема «в» рис. 8.15) таким образом, чтобы эти участки образовали замкнутую систему. При этом суммарный перепад давления равен нулю:
Ар - Арі + Ар2 = 0.
Будет ли движение среды по участкам 1 и 2? Раскроем выражения для сопротивлений Арі и Др2:
ДрТр.1 + Дрм. і + Друск.1 + Дрнив I + Дртр.2 + Друск 2 + Дрнив.2 = 0. (8.92)
Сопротивление трения и местные по своей физической природе требует затрат энергии на их преодоление при движении потока; сопротивление Ускорения может быть равно нулю при адиабатном потоке, больше нуля при нагреве и меньше нуля при охлаждении потока, в нашем случае происходит нагрев потока, Друск > 0; нивелирное сопротивление при подъемном
движении в вертикальной или наклоненной трубе положительно, энергия потока, затрачиваемая на преодоление этого сопротивления, идет на увеличение потенциальной энергии потока; при опускном движении нивелирное сопротивление отрицательно, т. е. потенциальная энергия потока превращается в энергию движения потока. Таким образом, нивелирное сопротивление (его называют нивелирным напором) на опускном участке может быть источником энергии в замкнутой системе типа «в» на рис. 8.15. Запишем выражения ДрНив в формулу (8.92):
- рсрлдН 4- рср. гдН 4- Дргр. і 4- Дртр.2+
+ Дрм.| + Дрм.2 + Друск.1 + Друск.2 = 0. (8.93)
Перегруппируем слагаемые этой формулы:
(Рср.1 - Рср.2)0# =
= ДрТр.1 + ДрТр2 + Дрм.1 4- Дрм.2 4- Друск.1 4- Друск.2- (8.94)
Левую часть выражения (8.94) называют движущимся напором 5ДВ:
SaB = (pcpA-pcp.2)gH. • (8.95)
Тогда
5ДВ = АРтр + + J2 Ару™- (8-96)
Возможны случаи:
1) участки 1 и 2 необогреваемы, q = q2 = 0; при этом рср. і = рср.2 и 5дВ.| = 0, движения потока по участкам 1 и 2 не будет;
2) на участке 1 q = 0, на участке 2 q2 > 0; pCp. i > Рср.2 и 5ДВ.2 > 0, движение потока происходит по направлению: участок 1 — участок 2 (против часовой стрелки);
3) на участке 1 q > 0, на участке 2 q2 > 0: pCp. i > Рср.2 и 5дв. з > 0, но 5дв. з < 5дВ.2, интенсивность движения будет меньше, чем в случае 2.
Следовательно, для увеличения движущегося напора SaR надо увеличивать рСр.| (qi уменьшать до нуля) и уменьшить рср. г (увеличивать q2). Подводимая теплота является внешним источником энергии, необходимой для преодоления сопротивления движению потока в замкнутом контуре. Движение среды по замкнутому контуру называется циркуляцией потока. Циркуляция, возникающая вследствие разности плотностей среды в необо - греваемых или слабонагреваемых трубах с опускным движением и в обогреваемых трубах с подъемным движением, называется естественной. Если в контур циркуляции встроить насос, то получим контур с многократной принудительной циркуляцией.
Все указанные виды движения жидкостей (однофазной и двухфазной) описываются уравнениями неразрывности, движения, энергии, состояния. Однако начальные и граничные условия для разных видов движения имеют свои особенности, что приводит к различным решениям основных уравнений. Особенности применения уравнений неразрывности, движения, энергии и состояния рассматриваются в последующих главах.