КОТЕЛЬНЫЕ УСТАНОВКИ И ПАРОГЕНЕРАТОРЫ
Режимы течения двухфазного потока
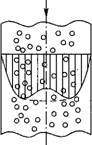
Рассмотрим изменение структуры двухфазного потока и его характеристик по длине I вертикальной обогреваемой трубы с подъемным движением среды. Принимаем, что интенсивность обогрева трубы по ее длине и периметру постоянна (qi = const). На вход в трубу (рис. 8.7) подается вода с массовым расходом G, кг/с, и энтальпией ho, кДж/кг, причем энтальпия на входе ho меньше энтальпии воды на линии насыщения h!. Величина недогрева воды равна AhHea = h! — ho. Учитывая, что изменение давления Ар в трубе мало по сравнению с его абсолютным значением р, примем давление р по длине трубы постоянным.
В общем случае течение двухфазного потока термодинамически неравновесное, и, как уже отмечалось ранее, для расчета истинных характеритик потока необходимо привлекать экспериментальные данные. В гомогенной модели потока он считается термодинамически равновесным, и для него можно расчитать ряд важных расходных характеристик. При этом уравнение энергии для участков с qi = const можно использовать в виде уравнений теплового баланса, а получающиеся в результате расчета характеристики будем называть балансовыми.
Балансовая (средняя) энтальпия потока /г6 = h на участке длиной I
Л6 = Л = А0 + ^, (8.68)
При qi — const линейно изменяется по высоте трубы (рис. 8.8)
|
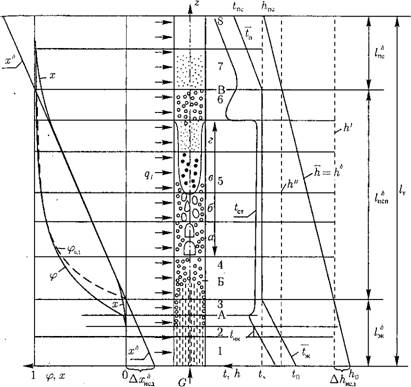
Рис. 8.7. Изменение режимов и параметров течения двухфазного потока по длине обогреваемой трубы. |
В сечении, где h = h по балансовым соотношениям должно было бы начаться парообразование. До этого сечения средняя температура жидкости £ж меньше температуры насыщения ts. Расстояние от начала трубы до точки закипания /т.3. (длина балансового экономайзерного участка Цк) мы Уже определяли (см. (8.38)):
L63K = k, = G-Ahnejl/qi. (8.69)
Балансовая длина испарительного участка lflcn (от сечения h — h! до сечения h = h", где h" — энтальпия пара на линии насыщения) определяется
Также из теплового баланса:
Tn = G(h"-h')/qi = Gr/m. (8.70)
Балансовая длина перегреватель - ного участка определяется необходимой температурой £пе (энтальпией /іпе) перегретого пара:
Lm = G{hM-h't)/qi. (8.71)
В сумме
/б _1_ /б I /б _ 7
Эк ^ исп ^ пе ~~
Балансовое массовое паросодер - жание х6 определяется по h
Хб = (h-hf)/r. (8.72)
Величина хб также, как и h, линейно изменяется по высоте трубы (qi = const). На экономайзерном участке х6 < 0, на перегреватель - ном — х6 > 1.
В реальном потоке при внешнем обогреве трубы температура по сечению не постоянна. Максимальная температура жидкости достигается у стенки и соответствует температуре внутренней поверхности стенки tCT. На рис. 8.7 показано изменение tcт по высоте трубы.
На входном участке 1 (до сечения, где tCT = ts) температура стенки и жидкости меньше ts. Это область однофазного потока жидкости. На участке 2 температура стенки выше ts, но парообразования нет, так как для начала кипения должен быть определенный перегрев жидкости. Парообразование на поверхности трубы начинается при tCT = іик, где tHK — температура начал кипения жидкости. На участке 2 жидкость не догрета до температуры насыщения, поток — однофазный.
|
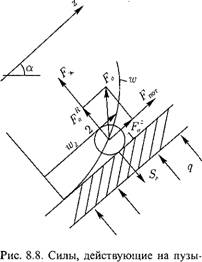
Рек пара в двухфазном потоке. |
На третьем участке балансовые значения температуры 1Ж и энтальпии h потока достигают значений на линии насыщения, при этом х6 = 0. В действительности, ядро потока еще не догрето до ts, а пристенный слой перегрет, т. е. tCT > ts. При tCT ^ tHK на стенке происходит образование паровых пузырей, в начале слабое, а после сечения А — интенсивное парообразование. При этом интенсивность теплоотдачи повышается, температура стенки незначительно уменьшается.
Что происходит дальше с паровым пузырем?
Формирование пузыря пара происходит вследствие роста его на зародышах, образующихся в микровпадинах твердой стенки. На пузырь пара радиусом гп, находящийся у стенки, действуют силы (рис. 8.8):
— динамический напор потока жидкости
T 2
^ПОТ^І^-ТГГІ (8.73)
Где — коэффициент сопротивления пузыря;
— сила Архимеда
Fk=gVn{p'-р"), (8.74)
Где Vn — объем пузыря пара; ее составляющие:
F= Fa • sin а — по направлению потока; F^ = Fa • cos о; — по радиусу трубы,
Где а — угол наклона трубы;
— сила поверхностного натяжения у основания пузыря
5б = сг • /нат, (8.75)
Где а — коэффициент поверхностного натяжения, /нат — длина линии действия сил поверхностного натяжения;
— аэродинамическая сила аналогичная силе Жуковского. Физический смысл ее заключается в следующем. Из гидродинамики известно, что полное давление в потоке жидкости р равно сумме статистического давления рст и динамического напора рдин:
2
Pw
Р = Рст+ Рдин = Рст + - у - • (8.76)
Запишем выражение для полного давления в точках 1 и 2, расположенных на противоположных концах диаметра пузырька пара (диаметр пузырька направлен по радиусу трубы):
Ft™ і
Pi = Рст. і - f —(8.77,a) / о
F) Wn
Р2=Рст2+Чг-- (8.77,6)
Принимая, что полное давление потока жидкости по сечению трубы постоянно, т. е. Pi = P2, получим
/2 /2 pwf PW2 Рст1 + "IT" = Рст.2 Н q •
Отсюда
/2 /9 pw о
Арст = Рсг.1 - Рст.2 = ^ - (8.78)
Для пузырька, сидящего на стенке трубы, w = 0:
/ 2
ДРст = (8.79)
Аэродинамическая сила действующая на пузырек пара, пропорциональна разности статических давлений Арст и сечению пузыря /п = 7гг„:
Ftk — а - Арст • /п, (8.80)
Где а — коэффициент, зависящий от формы пузыря, его размеров, скорости и других факторов.
При Fx = > 5б произойдет отрыв пузыря пара от стенки и он будет находиться в потоке жидкости.
Составляющая силы Архимеда направленная по оси трубы, изменяет скорость движения пузыря пара по отношению к скорости жидкой фазы. При постоянном движении потока сила наравлена по движению потока, пузырь пара имеет скорость w* больше, чем скорость воды wи относительная скорость w0TU — W* — w* > 0. Максимальная величина w0Tн соответствует вертикальной трубе (sinа = 1): FЈ = FA. При опускном движении потока сила направлена против движения жидкой фазы, относительная скорость w0TH < 0.
Таким образом, на 3 участке (рис. 8.7) образовавшиеся пузырьки пара из пристеночного слоя выносятся в холодное ядро жидкости, где они могут некоторое время (до конденсации пара) двигаться в потоке холодной жидкости. Потоки, в которых одновременно существуют пар и недогретая до ts жидкость, называют неравновесными. На третьем участке х6 < 0 (только на верхней границе хб = 0), но фактически у стенки х > 0 (поверхностное кипение), и истинное паро содержание ір > 0.
На 4 участке происходит постепенный прогрев ядра потока, толщина пристенного слоя с паровыми пузырьками увеличивается и в сечении Б пристенные двухфазные слои смыкаются. Поток становится термически равновесным.
На 3 и 4 участках паровая фаза существует в виде отдельных пузырей, находящихся в потоке жидкости. Под влиянием действующих на них сил пузыри стремятся расположиться в центре трубы. Такой режим течения двухфазного потока называется пузырьковым.
С ростом паро содержания количество пара в потоке увеличивается, а количество жидкости уменьшается. Пузырьки пара начинают объединяться в крупные конгломераты, и пузырьковый режим сменяется снарядным (участок 5,а). При этом режиме крупные пузыри пара («снаряды») по своим размерам соизмеримы с диаметром трубы. От стенки пузыри отделены слоем жидкости, а друг от друга — жидкостными пробками. Снарядный режим может существовать только при низких давлениях (до 3 МПа); при р > 3 МПа крупные пузыри пара не образуются.
Снарядный режим или (при повышенных давлениях) непосредственно пузырьковый, минуя снарядный режим, переходит в эмульсионный режим течения (участок 5,6). Эмульсионный режим характерен тем, что паровая фаза распределена в потоке в виде небольших объемов, между которыми находится слой жидкости.
При дальнейшем увеличении паро содержания и, соответственно, уменьшении водосодержания происходит разрыв жидких пленок между паровыми объемами, паровой объем образует в центре трубы сплошной паровой поток, в котором содержатся водяные капли. На стенках трубы движется жидкая пленка (участок 5, в). Такой режим носит название дис- персно-кольцевого (по распределению жидкой фазы).
На участке 5,г водяных капель в паровом объеме становится мало (испарились, выпали из потока пара на стенки трубы), жидкая фаза сосредоточена в виде пленки на стенке трубы — кольцевой режим течения.
Для всех режимов течения на участках 5, а, б, в и г характерно то, что паровая и жидкая фазы в ядре потока имеют одинаковую температуру, т. е. поток равновесный.
В конце участка 5, г по мере испарения воды жидкая пленка на стенке разрушается, образуются отдельные ручейки. Остатки воды испаряются или, частично, срываются с поверхности потоком пара и уносятся в центр тРУбы. Стенка омывается не жидкой фазой, а паровой. Теплообмен ухудшайся, наступает кризис теплоотдачи. Температура стенки резко возрастает в сечении кризиса теплообмена.
В закризисном участке 6 стенка омывается паром, жидкая фаза распределена в виде мелких капель в паровом потоке — дисперсный режим течения. Перенос теплоты от стенки к жидким каплям происходит за счет частично перегретого пара, при этом поток снова становится неравновесным Температура фаз различна). Средняя температура потока? ж равна практиче - В сечении В балансовое массовое паросодержание л;6 = 1, a h — h". Действительные значения х < 1 и < 1.
Дисперсный режим течения может распространяться и на участок 7, где х6 > 1, средняя температура потока tn > ts. В этом случае испаряющиеся капли воды какое-то время находятся в перегретом паровом ядре — неравновесный поток.
После испарения всех капель воды (х = 1) наступает режим течения однофазного парового потока (участок 8).
На рис. 8.7 показано изменение
Истинного паросодержания для адиабатного двухфазного потока область существования которого соответствует изменению X6 от 0 до -1. Действительное значение ср для обогреваемой трубы, также как и х, охватывает большую длину трубы; от х6 < 0 (участок 3) до х6 > 1 (участок 7). В этом диапазоне хб существует двухфазный поток.
|
|
|
4- |
|
2- |
|
Pw-10 , кг/(м~с) |
|
0,4 |
|
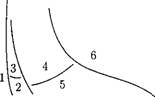
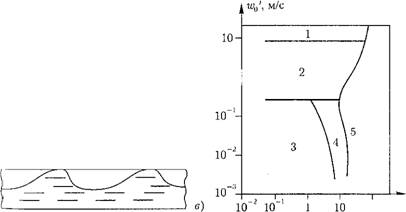
Рис. 8.9. Диаграмма режимов для вертикального двухфазного потока (р = = 7 МПа, d— 12, 7 мм): 1 — пузырьковый; 2 — снарядный; 3 — эмульсионный; 4 — дисперсно-кольцевой; 5 — кольцевой; 6 — дисперсный. |
|
—і— 0,2 |
|
0,6 о; |
Определить четкие границы существования рассмотренных режимов течения двухфазного потока сложно. На рис. 8.9 показана примерная диаграмма режимов для вертикального потока в зависимости от массовой скорости в трубе и доли паросодержания по ее длине.
|
|
|
|
|
|
|
|
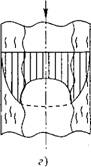
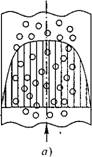
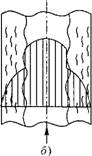
Рис. 8.10. Эпюра скоростей двухфазного потока: а и б — подъемное движение; виг — опускное движение; а и в — пузырьковый режим; б иг — кольцевой режим.
Распределение скоростей пара и воды по сечению в вертикальной трубе при подъемном движении потока зависит от режима течения. На рис. 8.10 показаны эпюры скоростей для пузырькового (а) и кольцевого (б) режимов.
|
|
|
А) 1- |
|
|
При опускном движении режимы течения аналогичны, но профиль скорости имеет другой характер. При пузырьковом режиме (рис. 8.10, в) по первоначальному профилю (пунктир) паровая фаза стремится к оси трубы, при этом за счет силы Архимеда движение центральной части потока замедляется и профиль скорости искажается (сплошная линия). Паровые пузырьки, находящиеся в центре потока, под действием аэродинамической силы
|
10- V, м/с Рис. 8.11. Режимы течения с расслоени - Рис. 8.12. Карта режимов двухфазных поем двухфазного потока в горизонталь - токов в горизонтальных трубах: 1 — пу - ных трубах: о — слоистый; б — волно - зырьковый; 2 —снарядный; 3 —расслоен - вой; в — поршневой. ный (слоистый); 4 —волновой; 5 — коль Цевой. |
Направляются от оси трубы в сторону возрастания скорости. В результате основная масса пузырей будет расположена в виде кольца на определенном Расстоянии между осью трубы и ее стенкой. При кольцевом режиме течения (рис. 8.10, г) паровое ядро имеет скорость меньше, чем пограничные с ним слои жидкой фазы.
В горизонтальных трубах распределение фаз по сечению зависит от соотношения сил инерции и Архимеда, определяемое критерием Фру - Да W2/gdBH. При малых значениях скорости потока это может привести к расслоению двухфазного потока на жидкую фазу и паровую фазу. При этом возможны режимы течения (рис. 8.11): слоистый (а), волновой (б) и
поршневой (я). По условиям температурного режима обогреваемых труб эти режимы не допустимы (см. главу IX). При увеличении скорости двухфазного потока имеют место режимы течения, аналогичные режимам в вертикальных трубах. На рис. 8.12 показано примерное соотношение режимов течения в горизонтальной трубе (wq и Wq — приведенные скорости воды и пара).
В трубах с углом наклона менее 30° (слабо наклоненные) режимы течения можно принимать аналогично горизонтальным трубам. Для сильно наклоненных труб (более 30°) режимы течения близки к режимам вертикальных труб.