КОТЕЛЬНЫЕ УСТАНОВКИ И ПАРОГЕНЕРАТОРЫ
Общие уравнения движения жидкости в трубах
Рассмотрим движение жидкости в обогреваемой трубе диаметром d (рис. 8.2). Считаем жидкость химически однородной, т. е. в ней нет примеси других веществ. Для описания состояния потока жидкости необходимо определить поля температуры Т, давления р и скорости w:
Т = Т(х, у, г);
W = w(x, у, г), где х, у, z — координаты, т — время.
|
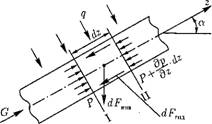
Рис. 8.2. Схема сил, действующих в потоке обогреваемой жидкости. |
Зная поля температуры, давления и скорости, можно рассчитать характеристики теплообмена и гидродинамики (тепловой поток, гидравлическое сопротивление и т. д.).
Поля температуры, давления и скорости называются нестационарными, если они зависят от времени, или стационарными, если Т, р и w не изменяются во времени.
Для определения Т, р и w используются уравнения неразрывности, движения и энергии. Эти уравнения получены из основных законов физики — закона сохранения массы, закона сохранения количества движения и закона сохранения энергии — с учетом специфичеких законов, характеризующих движение вязкой теплопроводной жидкости.
Запишем уравнение неразрывности, движения и энергии для одномерного потока (по оси z).
Уравнение неразрывности:
ОТ UZ
Где р — плотность жидкости, зависящая от Т и р.
При стационарном движении = 0 и уравнение неразрывности при
Мет вид
D{pw)z
TOC o "1-3" h z = 0. (8.3)
Dz
Таким образом, для установившегося движения при постоянном сечении трубы /, м2, и отсутствии притока (или оттока) жидкости, получаем
Pw = const, (8.4)
Т. е. массовая скорость потока pw, кг/(м2-сек), в указанных условиях есть величина постоянная.
Расход жидкости через трубу G, кг/сек, равен
G = pw • f. (8.5)
Уравнения движения. Выделим из потока жидкости в трубе (рис. 8.2) двумя сечениями I и II, расположенными на расстоянии dz, элементарный объем движущейся жидкости dv = f - dz. Применяя к нему теорему о количестве движения (изменение количества движения материальной системы равно сумме приложенных к системе внешних сил), запишем
Dl< = 4-mw = y^Fn. (8.6)
Dr
Для потока изменение количества движения dK массы жидкости, проходящей через сечение трубы /, и количества движения, связанного с изменением во времени плотности жидкости в объеме dv, равно
DK = a'f^f. dz + f-^.dz, ' (8.7)
Где а' — коэффициент, учитывающий неравномерность распределения скоростей по сечению трубы. Для развитого турбулентного потока о! = 1.
Внешними силами, приложенными к объему dv, являются: силы давления потока, силы вязкостного сопротивления, силы земного притяжения. Изменение этих сил на элементе dz в проекции на ось г: а) изменение силы давления:
DF, аш1 - f(p - (Р + |f • dz)) = -/ • |f • dz: (8.8)
Б) изменение сил вязкостного сопротивления (сил трения, сил гид- равлического сопротивления) dFnmp определяется касательным напряжением <тст у стенки. По экспериментальным данным
<^ст — А • pw2/8,
Где А — коэффициент сопротивления трения. С учетом этого
2
Pw
DFnmp = —<гст7ге/ • dz = — A • —— • nd • dz; (8.9)
В) изменение сил земного притяжения (нивелирная составляющая):
DFmn = —gpf - dz • sin а, (8.10)
Где а — угол между горизонталью и осью z (рис. 8.2).
Приравнивая (8.7) сумме (8.8), (8.9) и (8.10) и поделив обе части выражения на dz и /, получим
(„„
Уравнение (8.11) можно представить для установившегося потока в виде обыкновенного дифференциального уравнения:
2
Dp - f А^- • dz + дрsina ■ dz + d(pw2) = 0. (8.12)
Интегрируя уравнение (8.12) с учетом (8.4), получим формулу для расчета перепада давления на длине трубы м:
I (pw)wc р
Ар = А - •----------------- h Ідрср sin a + pw(w2 - wi), (8.13)
Где pep (аналогично, шср) — среднеинтегральное значение плотности (скорости); w, wo — значения скорости в начале и конце участка трубы. Выражение (8.13) обычно записывается в общем виде:
Ар = Дртр + АРм + Друск + Дрнпв, (8.14)
Где АрГр — сопротивление трения:
/ (pw)wCD
ДЛр = АІ • (8.14,а)
Арм — местное сопротивление (сопротивление входа в трубу и выхода из нее, шайб, поворотов и т. п.):
= (8.14,6)
Где — коэффициент местного сопротивления; ЛРуск — сопротивление ускорения:
АрУск = pw(w2 - Wi); (8.14,в)
Лрнив — нивелирное сопротивление:
Арнив = Igpcp sin а; (8.14,г)
Для вертикальной трубы при подъемном движении среды sin а = 1, при опускном движении sin а = —1.
Уравнение энергии. К потоку жидкости на участке dz подводится теплота QB в количестве
Qs = Qbh • пвн • dz = а2Пвн dz • (tBH - t), (8.15)
Где qBH — плотность внутреннего теплового потока, кВт/м2; П8Н — внутренний периметр трубы, м; а2 — коэффициент теплоотдачи от стенки к потоку жидкости; tBH — температура металла на внутренней поверхности стенки, °С; t — средняя температура жидкости, °С. Периметр трубы
Можно выразить через внутренний диаметр сівц, м,
Трубы:
Пвн ~ тг • dBn.
В (8.15) использовано уравнение теплопередачи в виде
Яви = Oi2(tBll - t).
Количество теплоты, переносимой потоком жидкости, изменится на отрезке трубы длиной dz на величину:
D(pwh) d{ph)
Где h — энтальпия жидкости, кДж/кг.
Уравнение (8.16) перепишем в другом виде:
D(pwh) d(ph) QBU сувиПвп dz
------------ 1--------- — —7- — ------- Z---- . . («.1 /)
Dz dr j f
Dh, 1 9{ph) qBHП вн dz,„ ,
Dz р™ ' ~ pw ■ / ' ^ '
Г/ Т
|
(8.20) |
Для установившегося потока ' = 0; тогда из (8.19)
Dh = ^внПвн dz
Dz pw • f
При qBH = const на участке трубы длиной /, приращение энтальпии потока жидкости равно
= = 1 (8.21) Р™ ' f
Обычно при расчете теплообмена в поверхностях нагрева парового котла задается (рассчитывается) величина теплового потока с наружной поверхности трубы qH. Определение внутреннего теплового потока qBH с учетом аккумуляции в металле трубы определяется по формуле
ЯвнПвн = <7нП„ - cMpMfM • (8.22)
Где П„ = 7гс/н — наружный периметр трубы, м; du — наружный диаметр трубы, м; см ~ теплоемкость металла трубы, кДж/(кг-К); рм — плотность металла, кг/м3; /м — поперечное сечение трубы по металлу, м2; tM — средняя температура металла (по толщине стенки) трубы в данном сечении, °С. Из (8.22)
DH Рм/м 9tsl /о
Яви = Ян ■ - т - - См— ТГ--
«ви Пвн ОТ
При стационарном режиме
<7вн = СЫ ■ - f - = Ян • /?. (8.24)
|
Учитывая, что pw - const, получим из (8.17) OZ ОТ f Или |
Wrh
Т. е. плотность теплового потока на внутренней поверхности трубы больше, чем на наружной поверхности в соотношении наружного и внутреннего диаметров /3.
Уравнения состояния. При решении уравнений неразрывности, движения и энергии необходимо знать такие физические параметры жидкости, как плотность р, теплоемкость ср, вязкость /і, теплопроводность А и др. Параметры р, ср, р, А в общем случае зависят от температуры и давления. Эти зависимости выражают уравнения состояния, которые могут быть представлены в табличном, графическом виде или в виде формул. Для реальных жидкостей уравнения состояния основываются на экспериментальных данных.
Начальные и граничные условия. При выводе уравнений неразрывности, движения и энергии не учитываются конкретные условия, в которых осуществляются движения жидкости и процесс теплообмена. Для решения задач о движении жидкости и теплообмене к основным уравнениям необходимо присоединить ряд условий, конкретизирующих задачу. Начальные условия состоят в задании полей скорости, температуры и давления во всем объеме рассматриваемой области (в том числе и на ее границах) в начальный момент времени. Начальные условия не задаются, если рассматривается стационарная задача. Граничные условия сводятся к заданию геометрической формы области и условий движения жидкости и теплообмена на ее границах.
Совокупность основных уравнений, уравнений состояния, начальных и граничных условий составляет замкнутую систему математического описания процесса движения жидкости и конвективного теплообмена в обогреваемых трубах.