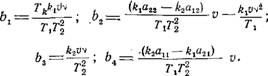ВЕТРОЭЛЕКТРИЧЕСКИЕ СТАНЦИИ

Периодическое изменение скорости ветра при постоянном моменте нагрузки

В действительности скорость ветрового потока в ре­зультате перемещений воздуха, связанных как с общи­ми атмосферными условиями, так и с вихреобразова - ниями, вызванными местными условиями у поверхности
земли, подвержена непрерывным пульсациям— поры­вам. Структурная характеристика порывов ветра чрез­вычайно разнообразна, но, несмотря на это, в аэроло­гии установлены некоторые приближенные закономер­ности, характеризующие ход порывов во времени.

Для уяснения характера движения системы при пульсациях скорости ветра рассмотрим случай, когда среднее значение максимальной • скорости ветра и ча­стота ее колебаний (частота порывов) могут быть вы­ражены приближенной зависимостью [JI. 10]:

V = 1,2и 4-7,2:

Макс ' CD I ' '

= 0,0038а' " і

Среднее значение порывов ветра; v — число порывов в секунду. На основании этих соотношений на рис. 2-23 построе - диаграмма, показывающая, в какой степени могут

Изменяться частота и крат­ность порывов для заданно­го диапазона рабочих ско­ростей ветра. Представим далее внешнее возмущение со стороны ветра в виде пе­риодического изменения ско­рости воздушного потока с частотой, равной частоте по­рывов ветра, и предполо­жим, что при постоянном моменте Мт колебания ско­рости - ветра происходят по синусоидальному закону Да = v sin v^,

Где v — амплитуда колеба­ния скорости ветра; v — частота колебания. При этом условии уравнения (2-34) запишутся в виде:

(р3 - f - ахрг + а2р - f а3) х1 = Ьг cos v* -f b2 sin vf,

Из максимумов скорости

Найдем частное решение для координаты В силу линейнос. ти уравнений (2-43) можно аналогично (2-35) положить, что

Хі—х.

Представив, здесь частное решение л:10 в форме

-£10 = <3 COS Vt 4 х sin

Где о и х — постоянные коэффициенты, подбираемые так, чтобы при их подстановке уравнения (2-43) обращались в нуль.

Заменяя в (2-44) л:1о его выражением (2-45), дифферен­цируя последовательно 3 раза и подставляя в (2-43), получим:

Р3х^ -}- v3a sin vt — tv3cosv/-|-

-f - at (p2Xtl — v2e cos v* — tv2 sin it) - f

4 a2 (px x — 5v sin 4t 4 cos vf) 4

4 «з j 4 з cos v^ 4 x sin vf) = bx cos чі 4 b2 sin vf.

Путем несложных преобразований это равенство приво­дится к виду:

(.Р3 + а, р2 4 агр + а3) хщ1 = [(v3 — а2у) % 4

+ (a, v2 — a3) з 4- bt] cos vf 4 [(ay — a3) % — (v3 —

— aav)<7-f-62]smv/.

Для того чтобы правая часть этого выражения обра - тилась в нуль, необходимо одновременно:

(v3 — a2v) x 4 (аУ — a,) a 4 bx = 0; (a. v2 - a,) (v3 - a2v) a 4 = 0.

Отсюда находим значения постоянных коэффициен­тов

_ (ч3 — a2i) Ь2 — (а, у2 — а,) 6, _ ° (V3 ~ a24f + (a, v« - а,)2 '

(у* —а, у)»1 + (а1у«—

Х (>3 — е2у)2 + (е, у2 — а3)2 '

Чтобы получить выражение для частного решения в раскрытом виде, надо пол ученные значения коэффи­циентов а и т подставить в уравнение (2-45).

Если до начала действия возмущающей силы систе­ма находилась в установившемся движении, то можно принять прежние начальные условия [*і(0)=0, *г(0) = — О, рхг(0)=0]. Исходная система уравнений (2-20) § 2-4 дает:

/tt,(0) = 0, р'хЛ 0) = ^-.

Подставляя эти значения производных в уравнения (2-37) и замечая, что

*1С(0) = о, Pxl0 (0) = vt, /Ле10(0) = - оЛ -

Получим следующую систему уравнений для определе­ния произвольных постоянных:

С + Л = -3;

— СЯ — Aw - f - Bq = — vt;

СЯ2 -f- А К - ?2) — 2Bqw=^- - f - v2a.

Определив произвольные постоянные, можно вычис­лить общий интеграл движения, который в данном слу­чае имеет вид:

Хг = Се~и-f e~wt (A cos qt--B sin qt) - f

+ (a cos v/ - f x sin v^). (2-47)

Первые два члена характеризуют свободные колеба­ния системы с затуханием, а третий член ■— вынужден­ные колебания от периодически меняющейся скорости ветра. Амплитуда свободных колеба«ий зависит только от начального состояния движения. В первый момент

Времени после нарушения установившегося движения амплитуда колебания системы будет определяться раз­ностью частот обоих колебаний, но после того как сво­бодные колебания исчезнут, она будет определяться величиной амплитуды колебания вынуждающей силы.

Напишем выражение для частного решения уравне­ний (2-43) по координате х2:

Х20 = Sj COS v/ - f - tj sin v/.

Применяя тот же метод, найдем значения коэффи­циентов и

__ (у3 —а2у)64 —(д, у2 —д3)63 .

• 1 (v3_a24)2+(aiv2_a3)2 .

_ (v3 —а2у)63 + (д1у2 —д3)64 1 (У3 — Д2У)2 + (д, У2 — Д3)2 '

При подстановке в исходную систему (2-20) § 2-4 начальных условий, принятых для координаты xt, полу­чим /72х,(0) = 0, и для определения произвольных по­стоянных будем иметь следующие уравнения:

С,+ 4 =-о,;

— С^, — AjW - f Btg ~ — vx,;

С^2 + А (ш2 — д2) — 2B, gw = v23l.

Общий интеграл движения по координате х2 может быть запиЬан в следующем виде:

Х2 = C, e~xt - f e~wt (At cos qt + Bt sin qt) - f

-f (^cosv^-f-^sinv*). (2-48)

Для наглядного представления о характере возму­щенного движения системы от периодически меняющей­ся скорости ветра рассмотрим несколько характерных примеров.

Пусть скорость ветра изменяется по синусоидально­му закону с амплитудой, равной v= ~ v0 и периодом

Г^Ю сек (соответствует частоте v = 0,628). Характер движения системы после начала действия возмущающей силы показан на рис. 2-24. Как следует из этой диа-

9—2412 129
граммы, несмотря на некоторое запаздывание действия регулятора по отношению к изменению скорости ветра, существенного увеличения движущего момента не на­блюдается. Максимальное значение движущего момента не превышает 1,35 (Мв)0.

Учитывая, что подобного рода системы содержат ряд существенно нелинейных функций, при выборе того или

Иного значения внешнего возмущения надо строго сле­дить за тем, как при этом могут измениться коэффици­енты уравнений упрощенной линейной системы (2-20) § 2-4.

Нельзя задавать такие внешние возмущения, кото­рые вызывают изменение этих коэффициентов более чем на 25—30%. В тех же случаях, когда требуется полу­чить характеристику точности регулирования при боль­ших внешних возмущениях, вызывающих значительные изменения коэффициентов, следует применять метод численного интегрирования исходной нелинейной систе­мы (2-14) § 2-4.

Увеличение скорости ветра после начала регулиро­вания связано с переводом лопастей на другие углы

Установки, а следовательно, и с изменением параметров Ул, Угр, k0 и др. В результате изменяется частота собственных колебаний системы. Чтобы выяснить, воз­можны ли резонансные колебания, надо проследить из­менение частоты собственных колебаний системы и ча­стоты порывов ветра в функции скорости ветра.

Случай, показанный на рис. 2-25, предполагает уве­личение частоты колебаний скорости ветра, равной те­перь v=2,l.

Характерным здесь является то, что наблюдается увеличение запаздывания действия регулятора, вслед-

М ij

Ствие чего движущий момент ветродвигателя растет бы­стрее, чем это имело место в предыдущем примере. В этом случае движущий момент достигает своего ма­ксимального значения 2,5 (-Мв)о в первую четверть се­кунды, после чего, несмотря на дальнейшее нарастание возмущающей силы, движущий момент быстро умень­шается. Установившиеся периодические колебания дви­жущего момента в данном случае происходят с ампли­тудой, равной 0,8

Как видно из приведенных по ветродвигателю ID-18 примеров, для системы прямого аэродинамического ре-

131

-гулирования динамическая неравномерность скорости вращения будет составлять не более ±'5%., а макси­мально возможное увеличение движущего момента не будет превосходить 2,5 {Мв)й.