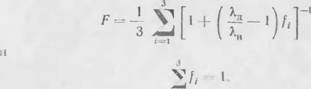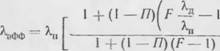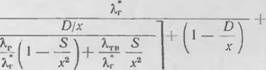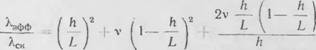ТЕПЛОФИЗИЧЕСКИЕ СВОЙСТВА ПОРИСТЫХ МАТЕРИАЛОВ
Обзор теоретических разработок по моделированию пористых систем
Теплоизоляционные свойства пористых систем привлекают к себе внимание чепых и инженеров начиная с конца прошлого пека.
В литераторе имеется довольно много данных по теплопроводности чистых материалов (кристаллических и аморфных твердых тел. металлов, газов, жидкостей) Рассматриваемые здесь пористые материалы представляют собой композицию ■ истых веществ. В природе много материалов, состоящих нз десятка и более различных компонентов, где очень трудно определить, в каком соотношении от; входят п как взаимодействуют друг с другом. Например, если чистый кварц—это только двуокись кремния, то базальт — jto композиция, состоящая из 12 компонентов п более. Однако многие материалы, используемые в технике, состоят из композиции двух или трех компонентов (например, вакуумнопорошкопая изоляции с добавкой металлического порошка в среде разреженного газа или порошок в среде бинарной газовой смеси). Из композиции двух-треч компонентов состоят такие. материалы., как бетоны, огнеупоры, некоторые растворы, смеси газов и др.
Исследование тепловых свойств пористых систем может проводиться дв>мя путями. Первый путь экспериментальное исследование теплофнзнчеекпх характеристик (теплопроводности, температуропроводности н удельной теплоемкости) пористых материалов при помощи известных методой, базирующихся па решении задач теплопроводности для тел различной формы. Хотя теоретические предпосылки при этом в большинстве случаев соблюдаются с некоторым приближением, этот путь дает возможность определить эффективные значения тенлофнзнческих характеристик с достаточно высокой точностью. Надежные измерения теплопроводности гетерогенных систем в широком диапазоне условии необходимы для понимания основных явлений переноса тепла в этих системах, тах как хорошо поставленный эксперимент дает возможность изучить зависимость тепловых свойств материалов от пористости, величины зерен твердой фазы, давления, температуры и других факторов.
Однако чисто эмпирический подход к проблемам переноса тепла в сложных системах, как и при рассмотрении других явлений, явно недостаточен. Акцентирование внимания на многочисленных эмпирических и полуэмпирическнх соотношениях без теоретического анализа, без рассмотрения взаимовлияния различных факторов уводит от понимания фундаментальных процессов переноса тепла, имеющих место в гетерогенных системах.
Поэтому весьма распространенным является второй путь, основанный па рассмотрении реальной структуры гетерогенной системы (число компонентов, пористость, размеры частиц и способы их контактирования между особой и др.), моделировании такой системы и последующего расчета ее эффективной теплопроводности для определенных реальных условий, определяемых давлением газа в системе, температурой, механической нагрузкой, наличием конвективной и радиационном составляющих теплопроводности и др.
Может показаться, что неопределенность формы и размеров частиц, разнообразие способов их контактирования меж ду собой, различная ориентация их по отношению к тепловому потоку и наличие большого числа неопределенных факторов делает процесс переноса тепла в твердых и зернистых гетерогенных системах безнадежно сложным, не поддающимся математическому описанию и теоретическому анализу. Однако Факты говорят об обратном. В настоящее время уже сущест вуют теоретические зависимости, позволяющие с большей пли меньшей точностью рассчитать эффективную теплопроводность пористых систем. Развитие работ и дальнейшие успехи в этой области могут привести к выявлению расчетных зависимостей для определения эффективной теплопроводности различных классов пористых материалов, сложных систем, что позволит сократить необходимость проведения сложных экспериментальных исследований, псиользовать последние в основном для проверки получаемых теоретических зависимостей.
Широко распространенным и достаточно эффективным методом теоретического исследования теплопроводности гетерогенных систем является применение для этой цели принципа обобщенной проводимости [9], базирующегося на аналогии между дифференциальными уравнениями стационарного по тока тепла, электрического тока, электрической и магнитной индукции, потока массы. Такая аналогия дает возможность использовать для расчета тепловой проводимости системы
Ачые соотношения электростатики и электродппа
Достаточно полная сводка формул, полученных па основе использования принципа обобщенной проводимости, приведена г. работе [9].
Необходимо отметить, что использование принципа обобщенной проводимости оказывается наиболее эффективным ї>сли оно сопровождается рассмотрением реальной структуры материала, оценкой пористости системы, размеров частиц и нор. способов контактирования частиц между собой, оценкой влияния кондуктнвной, конвективной и радиационной составляющих па эффективную теплопроводность системы. По пути анализа реальной структуры материала пошли многие советские и зарубежные исследователи [44, 225—228] При этом принимались самые разнообразные предпосылки о химическом чк. ше и структуре пористых систем, о форме, размерах п способе контактирования частиц, рассматривались различные V пособы н ориентации по отношению к тепловому потоку. Dei jth работы, результаты которых в ряде случаев пллюстрп - |юё.'пы многочисленными экспериментами позволили выявить влияние многих физических, химических, структурных и других
Иств системы на величину ее эффективной теплопроводности.
Очевидно, что чем больше рассматриваемая модельная структура соответствует реальной структуре пористого материала, тем больше расчетные данные по эффективной теплопроводности пористых систем будут соответствовать результатам экспериментальных исследований.
В качестве простейшей гетерогенной системы обычно pac - '.'..лтривается система, состоящая из чередующихся друг с тругом плоских слоев твердого скелета системы и газа, причем сто» могут быть расположены как перпендикулярно направленню теплового потока, так и параллельно ему. В первом случае эффективная теплопроводность системы будет минимальной п определяется выражением
TOC o "1-3" h z с;; .------------------------------------------------------------------- (2.1)
ЯАд -1(1 — П) Я,,, ' '
Во втором случае эффективная теплопроводность системы будет максимальной н равной
>'»ФФ ПК,, Г(-П)ХД. (2.2)
Здесь ли — теплопроводпость непрерывной фазы, Ад — теплопроводность диспергированной фазы, П — пористость.
Очевидно, что уравнение для Л^ф соответствует среднему геометрическому теплопроводностен двух фаз, а уравнение для — среднему арифметическому.
Теплопроводность всякой реальной пористой системы лежит между указанными экспериментальными значениями, поэтому ее можно представить как среднее геометрическое теплопроводностей двух фаз
^•эфф = ^д П ^н -
Это уравнение было предложено Лихтенекером [202] н. несмотря на крайнюю неопределенность модельной схемы, которую оно описывает, а также на то, что оно те учитывает многие факторы, имеющие место при переносе тепла в пористых телах, использовано рядом исследователей. Так, Вудсайд и Мессмер [l!)5J папіли, что для кварцевого песка, стеклянных шариков и свинцовой дроби в различных газах и жидкостях (фреон-12, вода и другие) уравнение (2.3) дает завышенные данные по сравнению с экспериментальными, если ад/а„>20. Лангтоп и Мэттыоз [203] использовали соотношение (2.3) для расчета теплопроводности окиси цинка и резины.
Годби и Зиглер [197] многочисленные теоретические решения для эффективной теплопроводности гетерогенных систем делят па две категории: решения, которые не содержат каких - либо допущений относительно температур и тепловых потоков, и решения, содержащие такие допущения. Соответственно первые соотношения называются «точными», а вторые — «упрощенными, приближенными». Точные решения соответствуют решениям, полученным на основе принципа обобщенной проводимости.
Одно из первых направлений в применении принципа обобщенной проводимости дал Максвелл [204]. Он рассчитал электрическое поле системы, состоящей из изотропной среды, в которую вкраплены посторонние частицы сферической формы Принимая, что расстояние между частицами велико по сравнению с размерами частиц, Максвелл тем самым пренебрег взаимодействием между частицами. Поэтому полученное им соотношение, которое имеет вид
» - І Г Хд + 2^-2(1-/7)(лн-Яд) ЭФФ ~ " L Яд-2Аи + (1 -/7)(ХВ-^ ]' ^
Применимо в тех случаях, когда пористость велика.
По пути рассмотрения электрического поля сложной системы и вывода соотношений, связывающих между собой напряженность электрического поля и диэлектрическую проницаемость, пошли и другие ученые. Бургер [205] и Фрик [206] рас-
Пространили теорию Максвелла на эллипсоидальные частицы. Соотношение, предложенное Фрнком, имеет вид
(2.5)
|
Для сфероидов (/j =- /0=/= f3)
|
Здесьj полуоси эллипсоида.
Коэффициент Г иредетапляст еобоїі оічіошеипе полных v ■ч-лпнх градиентов температуры в двух фазах. В случае, если. частицы имеют сферическую форму и уравнение Фрпка превращается в уравнение Максвелла.
Энкен [207] рассмотрел случаи, когда в дисперсном материал^ имеется несколько видов частиц различной формы.
|
|
Бруггман [208] вывел соотношение, которое применимо тля расчета проводимости смесей, состоящих из плоских час - іиц, частиц в виде вытянутых эллипсоидов, а также сферических частиц. Для последних это соотношение имеет вид
Рслсіі [209] представил теорию для конгруэнтных сферических частиц в кубической кладке Положив в основу уравнение Лапласа, выраженное через функции Лежапдра, оп рассмотрел граничные условия на границе между частицами и средой Оценивая теорию Максвелла—Эйкена—Бургера и сопоставляя расчетные данные, полученные на основании этой теории, с результатами многочисленных экспериментов, де Бриз [210] пришел к выводу, что эта теория дает хорошие результаты, если проводимость частиц меньше проводимости среды. Если же имеет место обратное явление, то чем больше отношение этих нроводнмостей, тем больше совпадают экспериментальные данные с теорией Бруггмана.
|
|
Де В риз рассмотрел также некоторые другие вопросы переноса тепла в зернистых системах, в частности влияние тсм-
поратурного скачка, малой площади контакта между частицами, эффект дистилляции воды во влажных материалах.
При расчете эффективной теплопроводности почв по соотношению Фрика де Вриз принимал fi = f2=l/8, /з = 3/4 и получил удовлетворительное согласование с экспериментальными данными [211].
Вудсайд и Мессмер [195] обнаружили, что соотношение Фрика с принятой де Бризом величиной ft хорошо описывает результаты многочисленных экспериментов, проведенных ими с кварцевым песком, стеклянными шариками и свинцовой дробью в различных газах и жидкостях, и в то же время дает заниженные значения Аэфф, когда Я. д/Яц> 100.
Уравнения типа Максвелла—Релея дают результаты, которые обычно хорошо согласуются с экспериментальными данными для ячеистых материалов и эмульсий. Горринг и Черчилль [212] сравнили литературные данные по 99 системам с результатами расчета, полученными по этим уравнениям, н нашли хорошее совпадение между расчетными и экспериментальными данными
Под приближенными понимаются решения, полученные при рассмотрении модели с некоторыми ограничениями, которые могут свести задачу расчета эффективной теплопроводности гетерогенных систем от решения дифференциального уравнения в частных производных к решению обычного дифферепші ального уравнения.
Согласно Годби и Зиглеру [197], приближенные решения могут быть двух типов: в одних — линии теплового потока предполагаются прямыми и параллельными, в других — изотермы рассматриваются как плоскости, перпендикулярные тепловому потоку. О решениях первого типа иногда говорят, что эти решения получены в предположении линейного теп лового потока либо нулевой боковой проводимости либо а предположении, что теплопроводность компонентов исчезающе мала в направлении, перпендикулярном тепловому потоку. Решения второго типа рассматриваются как решения, оси ) ваиные на допущении линейности изотерм либо бесконечной боковой проводимости либо на предположении, что теплопро водность компонентов в направлении, перпендикулярпом тепловому потоку, бесконечна.
Шуман и Восс [213] рассмотрели двухмерную модель, в которой твердые частицы ограничены разносторонней гиперболой. Полученное ими выражение имеет вид
|
|
Яй= ------------------ ,
TOC o "1-3" h z І, P(+P)(h-K) ln '
К I РІК К -
II
P 4- 1
П (P2 + P) In ---- P.
p
Обратив внимание на то, что расчетные данные Шумана и Босса превышают данные экспериментов. Вильгельм и др. [214] предположили, что это происходит за счет того, что не учитывалась проводимость в местах контакта частиц, и предложили свои модификации приведенного выше выражения.
Горрнпг п Черчилль [212] холят все гегерогетГные системы на гри категории: дисперсные, плотные слон и сплошные двухфазные материалы. Под дисперсными понимаются материалы, v которых одна фаза диспергирована в другой непрерывной фазе. Непрерывные двухфазные системы представляют собой материалы, у которых обе фазы непрерывны. Плотные слон могут рассматриваться как идеальный случай дисперсии с точечными контактами пли как предельным случаи непрерывной двухфазной системы, когда взаимные связи между частицами одной фазы исчезают. Горрннг н Черчилль показывают, что теплопроводность дисперсных гетерогенных систем может быть рассчитана соответственно для сфер п цилиндров но следующим соотношениям Максвелла:
, 2 -)- -—5 — %vJ 1------------------------- — ]
_ к 1„}
Оно было выведено при рассмотрении модели, которая представляет собой кубическую кладку частиц с поверхностями в виде параболоидов вращения, удовлетворяющих уравнению у Сх3. В вы - выражении (2.10) В — [%а/1(Хя — Ад)],/3 , х0 — половина ширины частицы. При Я, мДд>50 это выражение значительно упрощается
Аэфф = 1,92 [4/Р]"3. (2.11)
В некоторых работах делаются попытки учесть радиационную теплопроводность пористого материала. Так, Лое5 рассмотрел эффективную теплопроводность, обусловленную процессами копдукции тепла и излучения. Им предложена теория, связывающая эффективную теплопроводность с теплопроводностью твердой фазы с лучеиспускательной способностью по ьерхпостн пор, с их размерами, формой и распределением. II іу - чена также эффективная теплопроводность поры и эффект ив пая теплопроводность гетерогенного материала с различной ориентацией пор по отношению к тепловому потоку. Для расче та эффективной теплопроводности пористого материала Лоеб предложил соотношение, приведенное в работе [215].
Лучистая составляющая теплопроводности учтена в форм- ле, предложенной Г. М. Серых [216]:
Km (К. л I Ко, J ГП^ К, (1 - ГІР* ), (2 12)
Где Г — фактор формы.
Кунин и Смит [217] изучили вопрос об эффективной теплопроводности рыхлого слоя частиц, находящихся в среде неподвижного газа или жидкости. Показано, что эффективная теплопроводность такой системы является функцией теплопроводности твердой и жидкой фаз и объемных долей компонентов, а в случае, если заметную роль играет излучение,— также лучеиспускательной способности, средней температуры н диаметра твердых частиц. Принимая сферическую форму частиц, Кунин и Смит рассматривают следующий механизм передачи тепла: 1) перенос тепла через газ или жидкость теплопроводностью и радиацией; 2) перенос тепла через твердую фазу, который л свою очередь может происходить путем передачи тепла через контактные поверхности твердых частиц, теплопроводностью через газ или жидкость вблизи контактной поверхности, радиацией между поверхностями твердых частиц и теплопроводностью через твердую фазу.
Выведенное авторами [217] соотношение использовано дія расчета эффективной теплопроводности различных пористых сред и для сравнения расчетных данных с результатами экспериментов по определению теплопроводности различных типов песчаников, а также пористых металлов в различных газовых и жидких средах.
Предложенную модель они расширяют на уплотненные среды, полученные путем цементирования пористой системы или ее спекания.
Месамюн и Смит [196] рассмотрели вопросы контактной теплопроводности между твердыми сферическими частицами и показали, что контактная теплопроводность является функцией площади контакта, характеристик поверхности частиц, пористости и теплопроводности частиц. Результаты проведенных исследований дали возможность оценить величину угла контакта между твердыми частицами, который является характеристическим параметром рассматриваемой авторами модели и не является функцией ни теплопроводности твердых - частиц, ни пористости системы.
В работе Свифта [198] рассматривается порошкообразная система, состоящая из беспорядочно уложенных сферических частиц и имеющая пористость '10%- Автор аппроксимирует пу систему правильной ромбической кладкой частиц с пористостью 39.5% Рассмотрев элементарную ячейку в предположении. что линии теплового потока не искривляются. Свифт пошл C. IlMVIOlllVК) ІЛНИСИМОСП»
Л
Расчеты по соотношению [73] дают результаты, которые хорошо согласуются с экспериментальными данными Свифта. Он вывел также соотношение, которое можно применить для расчета эффективной теплопроводности аналогичных порошкообразных систем, состоящих из частиц, покрытых пленкой OKI1CH.
Годбн и Зиглер [197, 218] при выводе предлагаемой ими ■ анпсимости для эффективной теплопроводности порошков исходили из утверждения, что перенос тепла в порошках происходит следующими путями: теплопроводностью через твердую и жидкую (газообразную) фазы, в частности, теплопроводностью через твердую фазу, теплопроводностью через твердую и жидкую фазы последовательно или параллельно и радиацией между поверхностями твердых частиц. Эффективная теплопроводность порошка выражается как суммарная теплопроводность, являющаяся результатом действия всех перечисленных механизмов переноса:
Кй>Ф = ^тв + ^TU-Г Н" ^рад-
Рассматривалась следующая модель. В порошкообразной системе выделялся куб, причем все твер/Ше частицы, находящиеся в объеме этого куба, последовательно перемещались без чращепия в направлении двух осей. При этом получалось, что
часть куба была занята только твердой фазой, в то время как остальная часть заполнялась газом.
|
|
Сделав допущение, что контактная теплопроводность между частицами для рассмотренных ими порошков пренебрежимо мала, что изотермы представляют собой плоскости, перпендикулярные одной из осей куба, и рассмотрев тепловой поток, проходящий параллельно и последовательно через две фазы Годбн и Знглер, получим следующее выражение для эффективной теплопроводности порошка:
|
|
Іде х, D и S — характерные параметры рассматриваемой авторами модели; *—модифицированный коэффициент теплопроводности газа, определяемый по выражению
|
|
Здесь Я*—коэффициент теплопроводности газа; —кажущийся коэффициент теплопроводности газа, обусловленный па лнчием эффекта температурного скачка.
Второе слагаемое в соотношении (2.14) представляет собой радиационную теплопроводность. Здесь п — коэффициент преломления среды; о — постоянная Стефана—Больцмана; є — коэффициент излучения; 1—Я— объемная концентрация твердой фазы.
Соотношение (2.14) позволило рассчитать эффективную теплопроводность ряда порошков и сравнить полученные результаты с результатами проведенных авторами [197, 218] экспериментов. В работе указывается на их вполне удовлетворительное совпадение.
Большой интерес представляют собой работы, в которы. х сделана попытка рассчитать эффективную теплопроводность твердых одно - пли двухфазных снстем.
Так, соотношение Максвелла—Эйкена [219] дает возмож пость рассчитать эффективную теплопроводность двухфазной
системы, состоящей из непрерывной среды, в которой диспергированы частицы другой, меньшей по объему фазы:
I on I Xj/Xg
>м,_„_! zVk. • (2Л5)
2 L, + 1
В. П. Оделевекип [220] делит все гетерогенные системы на іi-ci типа: матричные, в которых одна фаза образует связную матрицу при любой объемной концентрации этой фазы, Польшей нуля, и статистические смеси, в которых частицы распределены хаотически, не образуя никаких регулярных структур. В качестве матричной он рассматривает систему, имеющую включения в форме правильных кубов, центры которых образуют простую кубическую решетку, а ребра параллельны.
|
1 |
Полученное расчетное соотношение
-oii>th
X, _J__________ 1 - Рд (2.16)
1 — 3
Применимо для случаев как малой, так и большой концентрации включений, а также справедливо для структуры с приблизительно равноудаленными включениями. Как указывает автор [220], выражение (2.16) совпадает с формулой Максвелла тля удельного сопротивления н после преобразований переходит в формулу Релея. Однако если формулы Максвелла и Релея применимы для ограниченного диапазона концентраций сферических пли круговых цилиндрических включений, то соотношение (2.16) применимо для включений, удовлетворяющих условию приблизительной изодиаметрнчпости в диапазоне объемных концентраций от нуля до 100% (табл. 6, 7).
Для статистических смесей В И. Оделевский получил соотношение
(Зо, — 1)^ -1 (Зи, — !)>.,
|
(Зоі-ПХ, - І - (Зо2-1)Я2 1 |
2 |
|
4 |
2 |
Пфф і
(2.17)
Представляют интерес работы Г Н. Дульнева, посвященные исследованию теплопроводности зериистых н твердых дисперсных систем. В работе [221] Г. Н. Дульпев и 3. В. Сигало - ия рассматривают идеализированную систему, или систему с дальним порядком в расположении частин. В качестве таковой
|
Таблица 6 Исходные данные для расчета эффективной теплопроводности
|
Выбрана тетраэдрическая упаковка сферических частиц Как и в других работах, анализу подвергается элементарная ячейка данной зернистой системы, строение которой выбрано таким образом, что сложение множества ячеек дает зернистую систему в целом. Это обстоятельство позволяет сделать вывод, что тепловые свойства ячейки будут идентичны свойствам всей системы. Для того чтобы приблизить рассматриваемую систему к реальной, учесть шероховатость частиц, область шероховатости авторы [221] рассматривают как ореол равномерной толщины вокруг сферической частицы, причем системы шар— ореол считаются уложенными плотнейшим образом.
Принимая допущение, что сами частицы не обладают теп ловым сопротивлением, авторы выводят соотношение, связывающее эффективную теплопроводность элементарной ячейки с тепловыми проводимостями отдельных зон элементарной ячейки: проводимостью через газовый ореол, через газовый микрозазор между контактирующими микрошероховатостями и др. Величина контактной теплопроводности выбирается из анализа экспериментальных исследований. Рассмотрена зависимость проводимости газа между мнкрошероховатостями от пористости материала. Лучистая составляющая теплопроводности газа оценивается посредством соотношения, полученного А. Ф. Чудновским [9]. Молекулярный перенос тепла в газе рассчитывается по формуле, приведенной в работе [222].
Авторами [221] получено следующее выражение для эффективной теплопроводности зернистой системы, в окончательном виде приведенное в [223]: для 26%<Я<74%
После ряда преобразований, направленных па упрощение математических выкладок, первоначальная изотропная модель была сведена к анизотропной типа параллелепипед в параллелепипеде [6].
Для уменьшения влияния анизотропности модели автором [11] проведено интегральное осреднение величины теплопроводности элементарной ячейки в определенном направлении.
|
— =І2 К |
Формула Р. С. Прасолова для расчета теплопроводности имеет вид
(3 2/7)2 I (1-Я)(0,14 + 2Я)Х л(1,14Я —0,14) 1Ъ (1,14/7 — 0,14)
|
КК + (0,14 + 2 Я) у |
|
Зх (1-Я) |
|
Цій JU |
|
К - к (2.22) К-К |
|
+ |
|
(1,14/7 — 0,14) |
|
Л. К, |
Где Я — пористость; ?tB — эффективная теплопроводность засыпки в вакууме (при —0), по существу характеризующая перенос тепла между контактирующими частицами.
Однако формула Р. С. Прасолова справедлива лишь в узких пределах изменения пористости.
А. Миснар [26] рассматривает гетерогенные тела как смесь вязкой фазы с частицами заполнителя. Эти частицы могут иметь самую произвольную форму, но для теоретического рассмотрения теплопроводности этим частицам придается правильная геометрическая форма куба, сферы, сдвоенной пирамиды. Кроме этого, полагается, что они равномерно распределены по всему объему и имеется тесный контакт между составляющими смеси, так что тепловым сопротивлением контактов мож:но пренебречь.
Автором [26] получен ряд формул для определения теплопроводности смеси в зависимости от формы частиц заполнителя;
Куб
(тепловой поток грани)
Днппрампда:
К+ J______________________ arctgR Л/ ■,
І КЯі-1 ^
Где V — объемное содержание; Я,, Хп — теплопроподности составляющих; Яв — теплопроводность тела.
Для твердых пористых материалов, когда велико.
|
(2.24) |
А. Мнснар предлагает использовать формулу
Г
К'% 1-f3.
В случае сыпучих материалов, когда контакт между частицами очень мал и воздух практически окружает их, справедлн ва формула (2.23) и (АвАа ^ 0)
^в А, | 1 4--------------------------- ~Т~)' (2.25)
V 1 —уз /
Іде г обозначает содержание твердых частиц, пористость ран - па I—і". Как видно из (2.25), теплопроводность материала в этом случае определяется теплопроводностью воздуха, однако это справедливо лишь при большой пористости, когда воздух плотно окружает твердые частицы.
В работе [26] проведено сравнение расчетных и экспериментальных [87, 88] величин (табл 8. 9) эффективной теплопроводности различных материалов. При анализе результатов видно, что с повышением пористости расхождение расчетных п экспериментальных коэффициентов увеличивается.
В общем случае, когда имеем дело с реальными пористыми или сыпучими материалами и нельзя точно определить, какой из предложенных формул (2 24 или 2.25) необходимо пользоваться, то действительная величина
Где a + b = 1, а и b являются структурными характеристиками материала п определяются экспериментальным пугем [26]. Таким образом. А. Мнет а ром предлагается полуэмпирическое соотношение, которое не всегда даст желаемые результаты (табл. 10).
Любопытно сравнить эффективную теплопроводность герметичных и открытых пористых систем. Герметизация пористых материалов препятствует циркуляции газа в порах под действием градиента температур. В открытой системе газ может свободно передвигаться и, следовательно, переносит
|
Коэффициенты теплопроводности сухого кирпича (сухой воздух) при температуре 20 °С [26J
|
|
Таблица 9 |
|
Коэффициенты теплопроводности сухого пенобетона (сухой воздух) прн температуре 20 °С [26]
|
Энтальпию. Теплопроводность открытых систем должна быто выше теплопроводности герметичных систем.
В соответствии с термодинамикой необратимых процессов в капнллярнопористых телах при наличии градиента температ р справедливы следующие уравнения [231]:
Для открытых пористых систем, когда нет внутри тела градиента давлений, вызванного градиентом температур, член Luu/T2 в уравнении фактически является коэффициентом теплопроводности
|
|
В герметичной системе неизбежно появляется граднепг давлений. Поток газа под действием градиента температур заторможен v/T=0. Тепловой поток для герметичной системы имеет вид
|
|
Соответственно эффективная теплопроводность равна
|
|
Т. е. для герметичной системы коэффициент эффективной теп лопроводности?/ всегда меньше "к для любого значения Luu. кроме нуля.
В работах [238, 239] применяется теория вероятности для описания хаотической структуры пористой среды. Методика расчета эффективной теплопроводности основывается на допущении параболического распределения прерывной фазы в непрерывной. Параболическое распределение выражается через постоянные, зависящие от пропорций составляющих.
Единичный кубический объем смеси делится на дифференциальные элементы, перпендикулярные к предполагаемому одномерному тепловому потоку. Каждый элемент состоит из непрерывной и прерывной фазы. Выражение для эквивалентною термосопротпвления в единице объема получают на основе аналогии между тепловым и электрическим потоком.
Формула содержит в себе константы параболы и теплопроводность составляющих.
Предлагаемая [238] модель расширяется далее для предсказания теплопроводности многофазных смесей для определенных случаев.
|
|
Эквивалентное тепловое сопротивление:
|
Re |
1) для случая яс>ясі (где — теплопроводность непрерывной фазы, К,/ — теплопроводность диспергируемой фазы)
2
V{C{ld-Kc)lKc bB(Xd-lc)]}
.1 З, IK ГіЯІ
|
В X tan 1 ■—- 2 |
|
/ |
|
С {К-К) K + B(Ki-h) |
|
1 ~ 8 (2.28) |
|
X. |
Где В и С — постоянные в параболическом распределении
В ] (ЗРrf/2), С -4} 12ДЗР,,)!
Н
* t
(V — среднее).
Р — объемная составляющая соответствующей фракции; 2) случаи
К, Ж
В [kd~Ці + [С (К - к ) J_ в
X 1п —-------- в г— =~ "Т--------------------- ' <2-29)
Где
«.--і-. К,
Если
17В ■ (2.30)
В табл. 11, 12 приведено несколько примеров сравнения расчетных данных по эффективной теплопроводности пористой среды, полученных различными авторами, с экспериментальными
Метод обобщенной проводимости для определения эффективной теплопроводности смесей с взаимопроникающими компонентами получил свое дальнейшее развитие, которое выразилось в уточнении влияния отдельных видов теплопереноса. Модель структуры с взаимопроникающими компонентами обладает рядом достоинств, таких, как изотропность, геометрическая наглядность, возможность изменения пористости от 0 до 1 без потери устойчивости.
Ю П Заричняк рассматривает модель пористой среды как структурі л-го порядка [28] применительно к структуре реальных зернистых и слабо связанных моделей.
:и
|
Таблица 12 Теплопроподность слосп со сферическими частицами
|
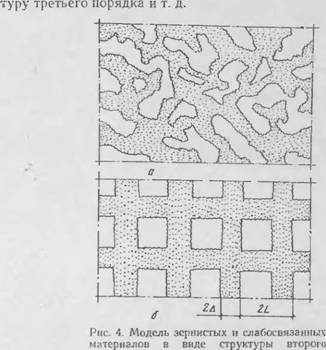
Так, в [28] предлагается реальную структуру представить п виде «каркаса»—«структура первого порядка», представляющая собой относительно плотную кладку постоянно контактирующих зерен и пространственной сетки более крупных пустот, пронизывающих каркас и образующих совместно «структуру второго порядка» с взаимопроникающими, непрерывными компонентами. Если же частицы каркаса сами являются пористыми, то система в целом представляет собой струк-
|
Порядка: С—тематическое изображение хаотической струк туры ренльпых мятер налов; о—плоское изображ пні упоридочепной модели структуры зернистых и слабосвяз<шных материалов |
Для уменьшения математических трудностей хаотическую структуру заменяют упорядоченной моделью, отражающей все основные особенности исходной структуры. Упорядоченная модель должна адекватно отражать структуру реального материала (устойчивость, изотропность, сохранение формы частиц) и корректность математического описания.
На рис. 4 показано плоское изображение упорядоченной модели отражения зерпнетых и слабосвязанных материалов з виде структуры с в іанмонроипкающнмн компонентами. При
этом предполагается, что каркас, образованный контактирующими частинами ненытянутой формы, представляет собоі'і упорядоченную трехмерную решетку с кубической симметрией и брусьями постоянного сечения. Пространство между брусьями и межзереиные поры в каркасе заполнены в общем случае газовой либо твердой компонентой нлп пх совокупностью.
Пористость рсальпоіі структуры меняется в достаточно широких пределах ш„=0,3-^-0,95, поэтому ее можно представить п виде сложной структуры второго порядка. В этом случае минимальные значения пористости всей системы будут определяться пористостью каркаса. Поэтому предполагается, что каркас образован наиболее плотной укладкой частиц одного размера шаровой формы с пористостью ш„ ~0,26=const. Пели пористость всей системы шп=0,26, то удовлетворительно работают модели, описанные в [5, 6].
Значения пористости >0.26 отражаются в виде структуры второго порядка вплоть до /;/„—»-1.
Предлагаемая модель [4] отвечает необходимым требованиям. в пси отражено наличие непрерывной последователь пост контактирующих частиц в любом рассматриваемом напр (Ленин, что обеспечивает устойчивость каркаса. Требования н ітропікк'тн обеспечивает кубическая симметрия прострапст - t і нон решетки с брусьями постоянного сечения, г. е. можно считать, что предложенная упорядоченная модель адекватно і тражает качественные особенности исследуемой структуры.
Для описания температурного поля в элементарной ячейке применяют теорию обобщенной проводимости, т. е. предполагают. что ячейка ориентирована относительно общего направлення потока тепла таким образом, что поверхности, параллельные потоку, являются адиабатическими, а перпендикулярные — изотермическими, причем температурное поле прп этом линеаризуется.
Элементарная ячейка имеет кубическую форму и образована пересечением двух изотермических плоскостей, перпендикулярных потоку тепла, и четырех адиабатических плоскостей, параллельных потоку. Часть внутреннего объема ячейки заполнена каркасом, который рассматривается как сплошное однофазное вещество с теплопроводностью Я.,,. Остальной объем имитирует пространственную сеть пор в структуре второго порядка С теплопроводностью Я,„|Г - Симметрия ячейки позволяет изучить перенос тепла в 1/8 ее части.
Ранее [8] было показано, что эффективная теплопроводность такой структуры определяется по формуле
Кп А
С,, — —• — геометрический параметр модели, свя-
К L
Заииый с объемной концентрацией компоненты, заполняющей поры в структуре II порядка тп11:
Решение которого имеет вид
С,, = 0,5 -(- A cos-------------------------- , (2.33)
3
Причем
0<mnII-<0,5, А — — 1, 0 = arc cos (I — 2mnI1),
0,5 <ш1іП < 1,0, Л = 1, в — arc cos (2mnI| — 1),
А значения В действительны при 270° «с 6 <360°.
Таким образом, зная объемную концентрацию компонент в структуре II порядка и их коэффициенты теплопроводности К И Я. ЩІ, но формуле (2.31) можно определить эффективную теплопроводность системы.
1. Объемная концентрация компоненты в порах /ппП определяется из следующих соображений:
Пористость всей системы— Мп
М
V
Пористость каркаса Мк ~ v„J(vT - f - ипн), тогда пористость стру ктуры II порядка
Mnll=vnll/v, (2.34)
Где v — общий объем системы; vn — общий объем пор в системе; vT — объем твердой компоненты; ипк — объем пор в каркасе; vnll—объем пор в структуре II порядка. Путем несложных операций находим, что
А1 „ = —— (,нп _ 0,26). (2.35)
Mi 074
А) вычисляем теплопроводность газовых компонент. В плоском микрозазоре Яп1 определяется молекулярной составляющей, т. е. Яп1 ~ Ят1 по формуле
Гі+ В - I 1 (2.36)
L Н.2 ftj
Или
V + 1
Где Хт — теплопроводность газа при нормальном давлении; у — отношение изобарной теплоемкости газа к изохорной; ах — коэффициент аккомодации, характеризующий долю обмена энергий молекул газа прн ударе о соответствующую стенку; Рг — кри-
V'c р-
Тернй Прандтля при нормальном давлении -- ЕИИ-■ # — давшії
Ленне газа-наполннтеля; А0 — длина свободного пробега молекул газа при атмосферном данлеиин и температуре: <- размер огра - ішчеііпоіо пространства (норы) в направлении переноса тепла 6; 2/tm; cpi — удельная теплоемкость газа; р; — плотность; v'— кинематическая вязкость при данной температуре. Например, для стеклянных шариков
D = 2,5 мм, К, ц {мм) ^ (8 — 10) - Ю-3, ■ «(6 -8) • 10 1
Г
■)) теплопроводность газа в сквозных норах каркаса равная геилопроводности пор в структуре II порядка Лп1[, определяется
К 0.45d / Т V
Всп с®,(2- с,,)(2 — е) V 100 | '
IHd( 1 — с„)
(2.37)
Где е—степень черноты поверхности часгнц.
В) рассчитываются параметры контакта частиц Номинальное пятно контактов г/2:
У2 = 2,3 ■ Ю-3 У 1,3Руд -}- 12р, д., (2.38)
|
— К, |
Малые нагрузки
Руд < 2 • 10* Л/и*- < 2 кс і см[1])
Їй
и модуль упругости
Є = е„ = 6,5 • 107 п/м2 (650 кг/см2),
Р„ — плотность засыпки, связанная с плотностью материала зерен и пористостью:
Мпрт = рт — рн,
Руд — внешняя нагрузка; Сс — вес вышележащего слоя, половина высоты которого hc.
В состоянии свободной засыпки Рул 0 и тогда
У = 5,2- 10-3,Лрн/1с - (2.39)
Размеры фактического пятна контактов у1 вычисляются по у1 — г/зІ^Л—связь размеров номинального у., и фактического пятна ух.
Необходимые сведения для определения контакта: плотность твердых частиц (>т; насыпной вес р„; пористость тн высота слоя /;,; относительное пятно контакта; величина внешней на грузки; модуль упругости є или е„.
Относительные размеры фактического пятна контакта в состоянии свободной засыпки:
Ул = 5,2 - Ю-3^рт(1 — mn)ht. Кть (2.40)
У, 5,2- И ть (2.41)
Где i| — сгпюсптельпая площадь контакта зависит от формы п размера микрошероховатости и т. д. при малых нагрзка (<2 кг/см2).
Для зернистых материалов характерны малые значения размеров пятна контакта
0<Уг< 1 • Ю-2.
Для практических расчетов
Ц)^ 0,017 + 0,4г/,, (2.42)
Г|> - - безразмерный параметр, характеризующий геометрию модели последовательно соединенных дисков, из которой определяется тепловое сопротивление газового зазора между сферическими частицами
0 2
Я,, 2 In--------------------------------- —----- , (2.43)
0,2 vM + h
H Л,„/0,5с/, v,
Vm [2]3
|
2,5 |
|
К'- |
|
=і + |
|
1 — Зг/і< І» |
|
-і 9,3- 10 Ч-3. |
|
(2.44) |
Тогда теплопроводность каркаса 2,2^
+ 2,2
1 1 0,8Ф + h h
Расчет теплопроводности каркаса весьма громоздкий, и, как показали проведенные расчеты, полученные результаты по приближенной формуле (2.45) мало отличаются от то того анализа (2.44).
Расчет X,- по упрощенной формуле: в порах сухой юзд ч
К ~= In 0,2 (0,2vM h)~ поры заполнены жидкостью
К; < К'
4,4Лж! п0,2(0,2Уж,- Л)-1,
Где
При кт>Хт, то по формуле (2.44) точную формулу для Х,( можно записать в виде
|
Іде |
2,5
1-З^ф-і +
Таким образом, зная параметры Af,, Я.,, и vI(, по формуле (2.31) определяется эффективная теплопроводность зернистой системы
2. Применение метода обобщенной проводимости для расчета эффективной теплопроводности
Пористых систем
Анализ существующих разработокло расчету теплопроводности различных материалов показывает, что метод обобщенной провочнмостн является самым надежным инструментом для создания моделей переноса тепла в различных средах.
Модель пористой системы. Рассмотрим па примере сухих зернистых систем применимость метода обобщенной проводимости для определения эффективной теплопроводности.
Эффективную теплопроводность зернистых систем следет рассматривать как функцию пористости, теплопроводности газа, заполняющего поры материала, теплопроводности газового микрозазора, контактной теплопроводности между частицами н теплопроводности самих частиц (конвекцией в порах пренебрегаем для частиц с L<4 мм)
. ^зфф __ W /7 ^г ^г-л ^к
^ск V ^ск ^ск ^ск '
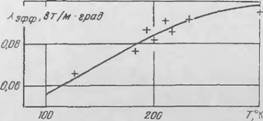
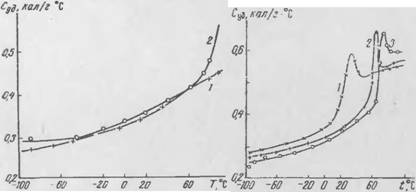
Кажущаяся теплопроводность воздуха как функция рас стояния между стенками поры, 7,=283°С [238], выразится: А/= 1 мм, 2, 4, 5 8, 10 мм соответственно, ?. = 0, 029; 0,032; 0,0405; 0,044; 0,0535; 0,0625.
|
|
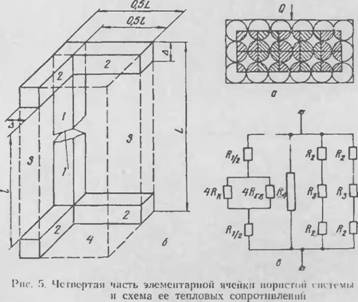
Предполагаем, что структура пористой системы монодисперсная (средний размер частиц одинаков), форма зерен близка к шарообразной, а укладка зерен рыхлая, как показано на рис. 5, а. Поток тепла предполагается прямолинейным.
Выделим в зернистой системе элементарную ячейку, тепловые свойства которой идентичны тепловым свойствам систе - л:ы'и целом. Считаем, что частички являются симметричными.
Введем следующие обозначения: / — основной размер пори; L — внешний размер элементарной ячейки; к=2Л — толщина и ширина стержня твердого скелета ячейки; v— объем элементарной ячейки; V — общий объем скелета в элементарной ячейке; v2 — объем второго компонента. Установим зависимость между объемной концентрацией (пористостью) П и отношением h/l. Так как элементарная ячейка симметрична, рассмотрим четвертую ее часть, объемы которой обозначим соответственно через г/, uj и v',. Очевидно, что
— L3, v = A2 (3L — 4 А). 4
Тогда
|
V v> . І Д |
|
І V |
Л И Л I
L 2(1 к) 1 2Д /
Обозначим Л/L — .v. тогда уравнение (2.48) можно записать в виде
4у3 — Зл~ - k 0; к = (2.49)
Решая ото уравнение относительно х п принимая во внимание, что
H х
I 0,5 —х
Получаем ілнпсішость f1=f(h/l), представленную ниже, т. е. П 0; 0,1, 0,2; 0,3; 0,4; 0,5; 0,0; 0.7; 0,8; 0,9; I. Соответственно кU оо; 4.21; 2,47; 1,75; 1,29; 0,846; 0,7; 0,507; 0,396; 0,241.
Приведенный вывод и зависимость аналогичны полученным в работе [224] для твердых пористых систем.
Сели принять, что линии теплового потока параллельны вертикальным образующим элементарной ячейки, то тепловые сопротивления составляющих 1/4 ячейки можно представить в виде
TOC o "1-3" h z L 2 2
R і--------------------- . R» ------------- , R-1 = —-— .
KtA2 KJ К*
|
(2.48) |
R> 4V К., - Щг. R. = Я, + Яш + *г. (2-50) V К J1
Где Rr.3 — сопротивление газового микрозазора на стыке двух частиц; RK— контактное сопротивление; RL — сопротивление, обусловленное сужением линий тока теплового потока в области, прилегающей к месту контакта; Rm — сопротивление мнкрошероховатости в месте контакта; R0 — сопротивление окисной пленки; kK — коэффициент, характеризующий сцепление микрошероховатостей двух соседних частиц.
В соответствии со структурой элементарной ячейки (рис. 5, б) и выражением (2.50) для термических сопротивлений можно составить электрическую цепь, показанную на рис. 5. о.
Эффективное тепловое сопротивление 1/4 ячейки равпо
R - 4 'ьфф — — — •
Йфф
Тепловые проводимости составляющих 1/4 ячейки и эффективную проводимость 1/4 части ячейки можно представить в виде
1 у2 _ 1
|
Ю3, о8фф -= ох + о2 + 2ст3, 1 |
О, ----------------- 7,--- , о., = т®; . 2о3 =
^+-7------------- J---- г 4L '
К + агз)
4LkKkm
(2.51)
Rl + R ш
Если в (2.51) подставить соответствующие значения проводи - мостсй, то после несложных преобразований получим
1 __________________________________ 12 _______________________ 1
------------------------------- h—— I о о
4 4L 4 4 і _____________ -
Kx№ ок + <тг. з KCJ rh
|
+ v2(l — h/Lf + |
Разделив это выражение на Xcl, L/4, найдем исходную формулу^ для расчета эффективной теплопроводности пористой системы
^зфф _ ___
Л " 1
|
(2.52) |
'"си ____
(h/Lf
Здесь
А ______________________ 1__________ .
+ /AV'io3 '
К* 4/гЛ,, L)
1 = I л. h hit —М___________ V V -
' ' I 1 «.,! ' Г 1 ' Г. З ,
1 4 И/1 Хса кС1(
Величина А отражает передачу тепла на стыке диух частиц через контакт между ними н газовый микрозазор. При отсут - СТ11ИП термического сопротивлении па стыке частиц А Он элементарная ячейка становится аналогичной той. которую рассматривал Г Н. Дульпев в работе [224].
Формула (2.52) применима для расчета коэффициента тсп- юпроводности порошкообразных материалов. Рассмотрим параметры, входящие в эту формулу.
Тепло от одной соприкасающейся поверхности к другой может передаваться в основном четырьмя самостоятельными процессами: а) теплопроводностью непосредственно через контакт; б) теплопроводностью через среду, заполняющую поры и пространство между выступающими шероховатостями .онтактнрующнх поверхностей; в) лучистым теплообменом между поверхностями; г) конвекцией газа в порах.
Ограниченные размеры нор и мнкрозазоров па стыке частиц препятствуют возникновению конвективных токов газа под действием температурного градиента. Известно, что при величинах (GrPr)<I03 конвективным теплообменом в норах можно пренебречь [33]. Это справедливо для частиц диаметром не более 4—5 мм. В данном случае рассматривается только теплопередача под действием температурного градиента. Как показано в [231], в некоторых случаях в пористых системах тепловой поток при наличии температурного градиента является причиной газового потока при наличии силы трения. Заключая газ в пористую среду с относительно большими порами, можно получить возрастание градиента давления, что вызовет в свою очередь поток газа в сторону, противоположную потоку под действием температурного градиента, и тем самым меньшит эффективную теплопроводность системы. Для герметичных пористых систем это уменьшение в некоторых случаях может составить 20%.
Описанная модель пористой системы позволяет получить значения эффективной теплопроводности, наиболее близко приближающиеся к экспериментальным данным.
В табл. 13- 15 показаны результаты расчетов по формулам различных авторов. Формула (2.52) удобна для расчетов и имеет 'остаточно простой вид. Существующее расхождение
|
Таблица ІЗ Сравнение эффективной теплопроводности, вычисленной по формулам
|
|
Таблица 14 |
|
Результаты экспериментальных исследований эффективных теплофизических свойств дисперсных систем [161]
|
Между рассчитанной эффективной теплопроводностью и экспериментальной можно значительно уменьшить дальнейшим усовершенствованием модели пористой среды; заменить прямолинейные брусья элементарной ячейки сферическими поверхностями, учесть адсорбцию газа на поверхности пор и ее влияние на эффективную теплопроводность и т. д.
Порошки. Хорошо известно, что поверхность контакта двух частиц представляет собой дополнительное сопротивление тепловому потоку от одной частицы к другой. Однако до недавнего времени этой проблеме уделялось мало внимания. Можно сослаться на несколько экспериментальных работ [184— 187, 193]. В настоящее время в ряде отраслей промышленности, в частности в энергетическом реакторостроении, имеются очень большие тепловые потоки от одной поверхности к другой путем непосредственного контакта. Следовательно, даже незначительные контактные сопротивления вызывают местные перегревы, что часто крайне нежелательно. В данной работе проведено исследование природы термического сопротивления контакта двух частиц в вакууме и получена модель данного явления.
В соответствии с работами [188, 189] тепловой поток, проходя от одной частицы к другой, сжимается в областях вблизи места контакта двух частиц. В области непосредственной близости к месту контакта происходит интенсивное взаимодействие фоиоиов друг с другом, что вызывает дополнительное термическое сопротивление.
Если представить пятно касания двух частиц в віще круга с радиусом г у, то тепловой поток внутри частицы проходи і через область, с жнвающуюся от площади /г2 до площа ш лr~t
В работе [189] дано определение коэффициента, учитывающего сужение проходного сечения для теплового поток 1
ИЫ:'
G (xL) = 1 + 1,40925 X + 0,29591 х3 +
+ 0,05254 л5 + 0,02105 г... ,
2 г
Где xt = " — коэффициент сужения. h
Соответственно тепловое сопротивление вследствие сужения проходного сечения для теплового потока, проходящего через две контактирующие друг с другом частицы, равно Rl = g{XL)
%гпКк
Для большинства реальных зернистых систем коэффициент близок к единице.
В работе [148] термическое сопротивление круглой контактной площадки на полуограинченном теле равно
Rl =
ЧЛк
При условии постоянства температуры по всей площади пло щадки и равно
Rl = 8/Зя2г, Л«
При условии постоянства теплового потока ша площадке. Эти выражения по величине близки друг другу
В работе |234] приводится отношение Rl. I2Rl дли шарообразных частиц
Rl SnL/2 2RQL 16 rn
|
V |
|
1 2 и |
P,„ (coscr) — P.,„)2(cosq.)]
/і=0
A [1 + P2n+1 (cos Ф)]; = sin ф.
Это выражение незначительно отличается от единицы. (При изменении 2 rJL от 0 до 0,4 RJ2 Rl меняется от 1 до 1,2)
Таким образом
Ras-------------------------------- [--- . (2.53)
2г ,Лс|(
Так как реальные частицы имеют различного рода микро - шероховатости, последние также вносят дополнительное сопро тнвлеине прохождению теплового потока. Сделаем следующее допущение: пусть микрошероховатость имеет какую-то высоту /іш и представляет собой цилиндр с площадью поперечного сечения пг*. Тогда дополнительное термическое сопротивление микрошероховатостей на стыке двух частиц можно выразить как
Яш (2.54)
Часто частицы, особенно металлические, покрыты пленкой окислов. Эта пленка может оказывать дополнительное терми чсское сопротивление R„ прохождению теплового потока. К сожалению, в литературе очень мало сведений о термическом сопротивлении пленок п их влиянии на эффективную тенлопро-
водность. В работе [198] наряду с изложением результатов экспериментального определения эффективной теплопроводности окисленных порошков урана и циркония делается попытка учесть роль окисной пленки при выводе теоретического соотношения. При этом эффективная теплопроводность системы рассматривается как функция теплопроводности твердых частиц, газа-наполнителя, окисной пленки, а также доли объема частицы, приходящейся на пленку. Эксперименты подтвердили пригодность полученного соотношения для расчетов эффектив иой теплопроводности окисленных порошков.
Во многих работах сопротивлением окисных пленок пренебрегают [190], либо их роль оценивается опытным путем.
Таким образом, контактное сопротивление зернистых систем можно предствить в виде суммы трех составляющих
RK = Rl + R,„ + R„,
А контактную теплопроводность как
К = • (2-55>
Для нахождения ЛаффЯ, к подставляем в выражение (2 52).
Помимо формулы (2.55), в расчетах для сравнения использовалась формула, предложенная Рнман-Вебером для определения контактной теплопроводности кубической кладки конгруэнтных сферических частиц диаметра L и радиуса контактного пятна гп:
К = Кк + — In — Г1 (2 56)
V 2гп Я R„ I
|
Г, |
Радиус контактного пятна для двух сферических частиц зависит от силы давления и может быть определен по формуле Герца [235]
- 0,725 |3 , (2.57)
Где
Т] =
Е
Принимаем S => ял,2,.
Для реальных частиц с шероховатой поверхностью площадь соприкосновения двух частиц зависит от характера шероховатости. Как показано в работе [188], при соотношении толщины к высоте, равном 0,1, для свободно насыпанного порошка
справедлива следующая формула для определения пятна касания частиц между собой:
Гя = 0.575 А (2.58)
В работе [230] контактная теплопроводность порошкообразных систем рассматривается как сумма контактной теплопроводности свободно насыпанного материала к'к, зависящей от геометрии частиц, их взаимного расположения, веса и пористости, величины 'к(Р), определяемой внешней механической нагрузкой Р:
К К к{Р), (2 59)
|
Пі" і. |
2.82 S
І Q /'„,*
Л... 1
К{Р) • ' Рл K (Р< 3- 10»
75 Q
I
T Q
Кс и /г„ — эмпирические коэффициенты. При изменении механической нагрузки от 4 • 10" до 12 ■ 105 н/м1 k„ изменяется почти линейно от 2,2 до 2,9. При изменении механической нагрузки от 105 до 3- 105 Кс изменяется от 0,35 до 0,45. В приведенных выше соотношениях
Q •
100 —Я
Значительную роль в передаче тепла при нормальном давлении играет газовый микрозазор на стыке двух частиц. Реальные частицы имеют шероховатую поверхность. Тепловую проводимость газового микрозазора можно выразить следующей зависимостью:
Or. (2.60)
Отношение li„,/L=Km-10_3 для частичек разных размеров является довольно стабильным.
|
Где |
Высоту микрошерохоиатостсй можно определять опытным путем но классу чистоты поверхности. Это особенно важно для металлических порошков там, где термическое сопротивление
|
Контактная теплопроводность перлита при различных граничных температурах 1I94J (толщина вертикального слоя между стенками 25,4 Ю"3 м, давление газа Я=Ю"3 н/м2, размер частиц -=0,5 Ю-3 м)
|
Частицы намного меньше термического сопротивления газо наполненного микрозазора.
Помимо мнкрошероховатостей, частицы имеют различного рода сколы и макрошсроховатости. В выражении (2.GO) тепловая проводимость газового микрозазора представлена в ви де проводимости параллелепипеда с высотой h,„ k, и площа дыо основания /і2, так как реальную площадь соприкосновения подсчитать очень трудно. Естественно, что теплопроводность газа в этом объеме будет несколько иной по сравнению с теплопроводностью газа в большой поре. Этот фактор учитывается эмпирическим коэффициентом kn, когда определяются молекулярная и лучистая составляющие теплопроводности в микрозазоре. Практика показала, что величина kn находится в пределах 0,5—1. Поскольку микропоры микрозазора не являются замкнутыми, туда неизбежно проникают молекулы, отраженные от поверхностей соседних частиц. Аналогичным образом проникает и излучение. Как кванты лучистой энергии, так и молекулы в данном случае проходят путь меньший, чем их пробег в большой поре.
В табл. 16 приведены расчетные величины для перлита, полученные по формулам (2.55), (2.56) и сопоставленные с экспериментальными данными [194]. Анализ расчетных величин по формулам (2.55), (2.56) показал, что формула (2.55) дает величины, более близкие к экспериментально полученным результатам, чем формула (2.56) Формулу (2.56) целесообразно использовать для ориентировочной оценки, когда неизвестно отношение hm/L.
В табл. 17 приведены величины А, к других параметров.
В работе [194] указано, что в температурном интервале 300—76 °К в глубоком вакууме (10^3 н/м2) через перлит проходит больший тепловой поток, чем в интервале ЗОО—20 СК
|
Контактная теплопроводность порошкообразных материалов при различных граничных температурах и давлениях газа 10 :| н/м'
|
Аналогично теплово» поток через перлит при граничных температурах 76—20 °К больше, чем при температурах 70—4°К. Это явный тепловой парадокс, который остался невыясненным автором [194], хорошо объясняется при рассмотрении структуры форм1 і (2.55), (2.56) для определения л,. Для температурно - іиапазона Ю0 -76°К средпеинтегральпая величина ЛСк ля SiOo. из которого получен перлит, больше, чем для диапа - .она і. пер ату р 300—20 °К [193]. Соответственно в диапазоне 76—20 К К-1 больше, чем в диапазоне 76 4 СК. Из-за этого ч нервом случае больше, чем во втором
|
(2.6!) |
Лучистая тсилопроподності» может быть найдена по фор-
/.," 2г-СГЧ,
Ирнведенной в [9], или по формуле, предложенной Лоебом чтя пористых систем
|
(2.62) |
Соответственно
2 rCT*k„l
І
В формулах (2.61) и (2.62) степень черноты поверхности материала является функцией температуры. Поэтому по теоретической зависимости Кр =f(T) можно лишь приближенно судить о величине радиационной составляющей. Однако для порошков со сравнительно малым диаметром частиц при ие глубоком вакууме н комнатных температурах влияние рачна - ционнон составляющей довольно незначительно. Влияние пз лучения является доминирующим фактором при глубоком вакууме и высоких температурах.
Существенное влияние на эффективную теплопроводность зернистых систем оказывает давление газа в порах. Согласно молекулярно-кинетической теории, теплопроводность газі является функцией давления, длины свободного пробега молекул, расстояния между поверхностями, обменивающимися теплом. Если размеры объемов, занимаемых газом, сравним со средней длиной свободного пробега молекул, па тенлонроиол ность газа большое влияние оказывает так называемый теми ратурный скачок. В зернистых материалах часто длина свободного пробега молекул газа соизмерима или больше размеров пор. В таких порошках уже при атмосферном давлении имеют место явления, наблюдаемые в разреженной среде В литературе опубликовано несколько вариантов теоретической зависимости теплопроводности газа от давления. Наиболее известные из них предложены Максвеллом, Кнудсеном, Смолуховским.
Здесь используется уравнение, опубликованное в работе [222], удобное с точки зрения практического применения
К =---------------- 3----- =------ .
2 —о, Кп
1 L+IZI^)
|
Рг |
K - f 1 V ах а2 )
Где
Кп= —, А --- Л - • - — — А„ —
Если принять ил — а.,, то это уравнение можно выразить в виде
К = --------------------------------- ------- , (2.63)
1 + В/HI
Где
В —^------------------------------ Рг_1Л„Я0.
K+ 1 а
К сожалению, в литературе очень мало данных о величинах коэффициента аккомодации при взаимодействии различных материалов с газами в широком температурном диапазоне [237]. В ряде случаев неизвестно, как изменяется величина Рг в широком диапазоне разрежения среды.
Довольно обширный экспериментальный материал имеется по эффективной теплопроводности зернистых материалов как
Г----- j----- 1---- ,----- 1---- функции давления газа в порах.
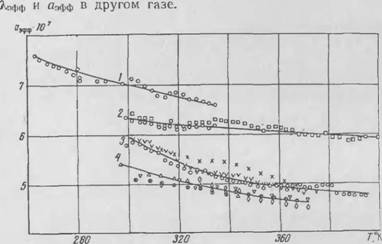
І І І ™:<!чі Экспериментальная зависи
Мость /in =/(//) в. полулогарифмических координатах нме - .ч - пні S-обра той кривой. Особенно много экспериментальных данных получено для рп. ілич'них ПНІОІ! нлкуумпо-но
Ропікоиой ii іоляцніі.
Глце С мо. ту ховскиГі и Дыо - ар чамегилп. что при занолпенні прос гране та между степками некоторых сосудов мелкодисперсными порошками полу-
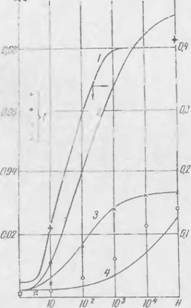
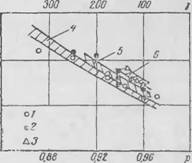
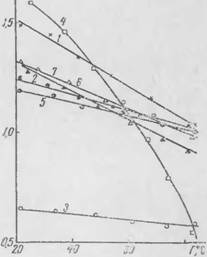
Piv Г>. З. пиіі'іиі. кті. іц-мстіїллії
■ич'кііч <г|>шігіід м;іті'|>н;имш or д;ін jk-іііія ii:
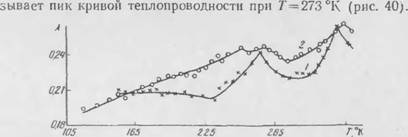
І - ьпарисвый песок {L 0,4X10 3 м); 2—по - рошкообрлный плексиглас (/.—БОХЮ"5 .«): '-перлит (L=0.E < I0'3 лі): 4 — кремнегель IL "ivio 6 л): (/—экспериментальные точки отве ствепчо чрнн. їх /, 2. 3. 4)
Чается почти такой же эффект, как и при высоком вакууме между стенками с малой степенью черноты.
Сравнение экспериментальных и расчетных зависимостей /.uM> = /lW) (рис. 6) и табл. 18 дало их хорошее совпадение. Эксперименты н расчеты показали, что в мелкодисперсной ва - vvmih і-поропіковоп изоляции целесообразно использовать разреженный газ с максимальной длиной свободного пробега молекул (например, гелий, водород), хотя теплопроводность ■ их і. і «>в ошоептелык) высока.
|
|
налпз S-образиых кривых показал, что при малых разрежения іффсктнвпан теилопронодность зернистых систем часто не „ависит от давления до тех пор, пока давление не снижено до величины, при которой длина свободного пробега молекул становится соизмеримой с характерным размером пор (Кп I) При дальнейшем понижении даилетшя тенлопровод-
иость засыпок изменяется пропорционально изменению давления. Наклон 5-образных кривых зависит от размера пор и характеристик газа.
При исследованиях в области низких давлении в ряде слу - "аев следует учитывать существование термомолекулярноіі диффузии, в результате которой истинное давление в слое пористого материала может быть различным. Величина поправки на термомолекулярную диффузию измерена в работе [240] как функция давления температуры, диаметра каналов и рода газов.
Таким образом, в формуле (2.52)
К =--------------------------------------- + . (2-64)
1 + В/HI
К, ---------------------------------------- I К,- (2-65)
"я 1 + BIHkJ '-3
В качестве примера произведем расчет эффективной теплопроводности перлита, экспериментально определенная зависимость h«„i,=f(H) которого приведена в работе [194]
Диаметр частиц вспученного перлита 0,5 мм; пористость /7=0,947; h/l—0,14; h/L = 0,123; толщина вертикального слоя между стенками со степенью черноты 0,8 равна 2,54- 10 2; граничные температуры 304—76 СК. среднеинтегральпая теплопроводность для указанного диапазона температур 1,2!) вт/м-град; среднеиитегральная теплопроводность воздуха в указанном диапазоне температур 0,0168 вт/м-град; давление окружающей среды 102 н/м2; В/Н1—2,19; принимаем Я. г=Лг3; плотность у— = 1400 н/м3; £ = 5,49-1010 н/м2; р = 0,25; /i = 0,3; b=4.
Имеем Я? = 0,0168 =52,7- 10~4 вт/м-град, 1 + 2,19
КРГ = 9,2 10-2 • 27 0,41 • 0.25 • 10~3 = 2,55- КГ4 вт/м-град, = (52,7 + 2,55) Ю-4 = 55,25 • 10~4 вт/м-град, = 55,25-10-4 1()_4
Г 1,28
Радиус пятна касания определяем по формуле (2 58) гп = 0,575 - 0,25 • 10—1 х
/ 0.025-1400-4,2-0.94 q 72 . I0-w, V 5,49-1010-0,3
|
Таблица 18 Эффективная теплопроводность некоторых зернистых материалов в воздушной среде различной плотности
|
|
Г>8 |
F 42,2-10^»-(1 — 0,123)2 +
-I------------------------------------------------------ 2------------------------------- = 121 • 10-
1+0,14 + 1/(43,2- 10"4-0,123)
Яафф = 1,28 • 121,0- Ю-4 = 155 • 10>~4 вт/м-град,
ХЭ1(СП = 155,10 * втім-град.
В табл. 19 приведены величины ХЭфф ряда зернистых неметаллических материалов в атмосфере различных газов нормального давления. Экспериментальные величины лг, фф сопоставлены с расчетными по формуле (2.52), а также по формулам Максвелла и Бруггмана для широкого диапазона изменения пористости (35-^-98%)-
Как видно из табл. 20, формула (2.52) дает хорошее совпадение результатов расчета с экспериментальными данными.
Рассмотрим применимость метода обобщенной проводимости для определения эффективной теплопроводности метач - шческих порошкообразных систем. Металлические зернистые системы широко используются в технике в качестве ТЄПЛОЕОІ1 пзолянии при высоких температурах, а также в качестве изоляции, позволяющей выдерживать большие механические нагрузки благодаря высокой механической прочности. Часто металлические засыпки используются в атмосферах различных активных и инертных газов. Для металлических засыпок эффективная теплопроводность намного меньше теплопроводности металла, из которого они сделаны. Если рассматривать НеЛНЧННЫ ОТПОШеННЯ Аск Ар, то для теплофизоляционных материалов они составляют 10—300, а для металлических материалов могут доходить до 1500—2000 и более. Естественно, чго во многих случаях теплопроводность таких металлическич систем зависит от сопротивления контакта между частинами, проводимости газового микрозазора и в малой степени от термического сопротивления самих частиц. При расчетах металлических засыпок при соотношении ХСь-Дг>700 1000 термическим сопротивлением самих частиц можно пренебречь. В этом случае формула (2.52) приобретает вид
|
KK -- 1,5, km — 1, = 1,4 ■ 10 :i вт/м-град, ^эфф _____________________________ !______________ _______ |
|
К, І 66 + |
|
• 0,0151 • 10-* |
|
1,4 10"3 43,2-10~4 1,28 4,1 - 1,5 |
Где /.,; определяется по формуле (2 55).
Т, і б л и ц, і 1')
|
Теплопроводность зернистых материал»»
|
|
Maitpi и |
Росч< тные величины, рпі,'м - гра)
.<5
|
300 К 300 К 100 К Т 300 к 300 ск 100 к К[239] К[239] К[239] К [239] К 14] 1194] [194[ |
Стеклянные шары — воздух [24] Стеклянные шары — воздух [77] Стеклянные шары —Н2 |241] Стеклянные шары —Н [77] Стеклянные шары —СО, ['">9] Кварцевый песок — воздух, Т Кварцевый песок — возд х, Т Кварцевый песок Т — 300 К Кварцевый песок — гелий, Т = Плексигласовые шары — воздух, Плексигласовые шары — Н Т = Плексигласовые шары —Не, Т Перлит — воздух, Т — 77 — 300 Перлит — воздух, Т = 77 — 300 Перлит — воздух, Т = 77 — 300 Перлит — воздух, Т = 77 — 300 Перлит — воздух, Т = 77 — 300 Перлит — Н2, Т = 77 — 300 "К Перлит — Не, Т = 77 — 300 К Диатомовая земля — СО> [242] Диатомовая земля — СН4 Диатомовая земля — газол [242]
|
0,134 1 0,138 0,460, 0,480 0,080 і 0,148 0.138 0,105 0,247 0,079 0,177 I 0,108, 0,021 | 035 0,022] 045 , 0,025 | 0,019 0,023 0,137 1,180 |
|
3.8 0,10 4 0,16 |
|
,029 024 147 ,139 |
|
40 35 40 35 40 35,4 37,7 47 38 40 40 40 98 96 92 95 95 95 95 71 71 71 |
|
10,180 0,159 '0,460 0.360 0.234 '0,440 0 415 0 370 ,0. 303 0.095 0,141 0.058 ,0,0285 0,0351 0,0460 0,0325 0,0277 0,146 0,126 0,099 0 0152 0.134 |
|
016 0.17 026 ,0.78 0.435 0,150 |
|
026 027 070 026 16 070 02 02 02 016 026 123 105 0163 0384 0314 |
|
0,485 0,059 0,050 0,050 |
|
0,500 0,005 0,5 0,5 0,2 0,2 0,2 |
|
033 026 144 126 100 162 142 |
1,09 0 ,09 0 1,09 0 1,09 0 1,09 ,0, 1.37 0, 1,37 0 1,37 0 20,5 0, 0,19 0. 0,19 0, 0,14210, 1,28 І0, 1,28 0, 1,28 ІО
1,28 1,28 1,28 1,28 1.51 1,51 1,51
|
,344'0,78 |
|
0,940' 0,845 I 0,9381 0.782 1,800 1,070 1,035 | 0 9-Ю 1 ,080 1,050 0,945 0,906 |
|
,15 ,0 .75 ,93 .18 |
|
1 ,48 1 ,95 1.29 1 ,52 1,770 1,350 1,205 I,065 |
|
1 ,000 1 ,020 0,965 0.065 0,013 1,0 0,99 0,94 0,945 |
0,63 0,92 0,66 1.47 1.57 1,56 ,53 '2.06 23 ' 1,04 2 1,02 785
536 0,020 0.35 595 84 71 205 065
106 0,105
|
Таблица 20 Теплопроводность металлических порошков в различных газовых средах
|
Вое предыдущие рассуждения о путях передачи тепла п зернистых системах применимы и п данном случае. Одним из пап более существенных факторов передачи тепла в металлических засыпках при нормальном давлении газа в порах является теплопроводность газового мнкрозазора, по сравнению с которым проводимость тепла газом в поре довольно мала. Для определения эффективной теплопроводности металлических порошков очень важно знать чистоту обработки поверхности частиц, высоту мнкрошероховатостей и силу прижатия частиц друг к другу Высота микрошероховатостей определяется по классу чистоты обработки материала или опытным путем с использованием электронного микроскопа.
Как пока алп исследования, отношение высоты мнкрошероховатостей к диаметру частиц является довольно стабильным. Д. іїГ некоторых металлических засыпок оно равно ^2-4)10 3 (свинцовые п стальные частицы). При расчете ряда металлических засыпок это отношение принималось равным 3-10~3 п - =1.5 (табл. 20).
I» форму.1С (2.60) миффпцпен г А',г отражает взаимное рас положение мнкрошероховатостей двух частиц, находящихся в контакте друг с другом. В подавляющем большинстве случаев >' | ен 1.5- 2. Для стектяппых шариков отношение /zm/L равно (-1 5) -10 3. Оптические измерения высоты її ці для шарим и диаметром 2- 2,5 мм дали величины (8 - Ю) -10 3 мм При расчете засыпок нз стеклянных шариков в различных га- < ш. ср дах принималось hm/L-10 3 равным 4 при k„ равном 2 (см. табл 19).
В СВЯЗИ С ЭТИМ, безусловно, является целесообразным проводи II) систематические измерения отношении /іім/L для засы - по1 из различных материалов и составить таблицы зависимости /(, ,/L для широкого класса материалов. Это в значительной степени уточнит расчет эффективных тенлофизических свойств порошков.
На контактную теплопроводность засыпок некоторое влни пне оказывает механическая нагрузка. Зависимость X,; = f(P) от механической нагрузки можно определить по формулам (2.55), (2.56) и (2.59). Следует отмстить, что механическая ааіру іка мало изменяет пьют мпкротсрохова roc гей и преде л упругой деформации частиц.
Экспериментальное исследование проводимости контактных поверхностей, а также проводимости контактных пар частина плоская или выпукло-вогнутая поверхность проведено в работах [193, 245].
В ряде случаен металлические заеыпкп следует рассчиты - ьать ш> формуле (2.52), если отношение лежит в преде
Лах <500.
В качестве примера рассмотрим эффективную теплопроводность Сталиных шариков в воздухе (экспериментальные данные приведены в работах [243, 244]).
Расчеты производим по формулам (2.52) и (2.66), так как АСКД0 в данном случае равно 1475.
Исходные данные: L = 3,18- Ю-3; П -38%; 1 38,4; к„ = = 0,026; Г=320°К; h/l =1,34; h/L-— 0,573; Р = 105 н/м2-, vr = = vr. g = 0,677-ЮГ3; km — 3; /гк=1,5; Хк=0,08.
По формуле (2.52)
_______________________________ 1__________________
1 1 1
It| Ф 1 і________________________ і о й77
"Т 0,5732 0,03 , 0,677-10~3-0,5732 ^ '
'•ск ' -----------------------------------------------------
38,4 ^ 4-3-10—3 -1,5
10~3-(1—0,573)2-| --------------------------- =----------- 18,6-10-*
1 + 1,344--------------------------------------------------
0,677-10~3-0,573
ХЭ(,ф = Хск=13,6-10-3 38,4-13,6- Ю-3 = 0,523.
По формуле (2.66):
Л3фф = 0,026 —^— 0,5782+0,03+0,026 (1—0,573)2 + 4,3-1,5
+0,026-0,573=0,524.
Экспериментально измеренная теплопроводность Яафф равна 0,525 вт/м-град.
По формуле (2.66) расчеты значительно упрощаются.
В табл. 20 приведены экспериментальные величины Я:,ф1р ряда металлических засыпок в различных газовых средах нормального давления. Экспериментальные данные сопоставлены с расчетными по формуле (2.52) для водорода и по формул» (2.66) для других газов, а также с данными по формулам Максвелла п Бруггмаиа. Более близкое совпадение результатов получается по формулам (2.52) и (2.66).
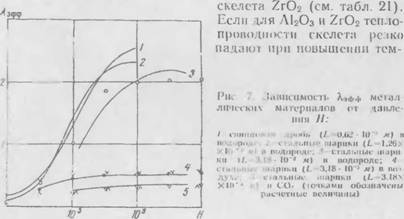
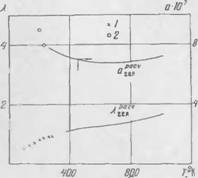
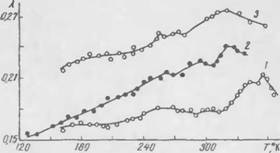
На рис. 7 представлены экспериментальные и расчетные зависимости /^фф=f(H) для некоторых металлических засыпок.
Большие величины отношения ХСк/Хг характерны ие только для металлических порошков, по и для порошков, приготовленных из окислов металла. В работе [197] приведены данные по эффективной теплопроводности окислов А1203, MgO и ZrO в виде порошков в широком интервале температур. На рис. 8—
10 и » ViH>л. 21 экспериментальные данные сопоставлены с расчетными. Расчеты были произведены по формулам (2.52) и (2.66).
У кристаллических порошков нз окислов металлов отношение высоты мнкрошероховатостей к характерному размеру частиц равно /!m/L=4-К)-3. Коэффициент кладки частиц был выбран, как и в большинство других расчетов, равным 1.5.
|
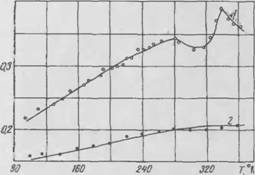
Рис. 8. Расчетная эффективная теплопроводность М<>0 и но. ілуко (urjiH-граО) (точками '.ібози. і'іенм актори мен і а. іьііис іаішие |І97] для различной пористости): |
|
/ .к»,. •' жк, .і и»",. , і ил, |
Любопытно отметить тот факт, что теплопроводность скеле - іа АЬО и AgO значительно отличается от теплопроводности
|
|
Атчры. то для ZrC2 наблюдается слабое возрастание Я. с, с ростом температуры. Однако благодаря высокому термическому сопротивлению газа ь порах эффективная теплопровод - гь порошков медлоппо і ізрастаетс повышением температу
А
Ры. Если для AgO при температуре 373 °К отношение /г,//.г = = 760, то при температуре 310 °К ЯСкМг=232. В первом случае для расчетов можно пользоваться формулой (2.66), во втором случае расчеты необходимо производить по формуле (2.52).
Порошкообразные смеси. В настоящее время обострился интерес к изучению свойств смесей различных порошков, использование которых в качестве тепловой изоляции оказывается весьма перспективным Различные виды порошков, в частности порошков, твердые фазы которых состоят из аморф-
|
Рпс. 9. Расчетная эффективная теплопроводность (втім • град) Zr02 в воздухе. Экспериментальные данные 1197] для пористоеш: /—30%; 2—36%: 3—42 |
Л Зфф
|
____ |
—-/ г |
|||
|
"ь |
' ° ° |
|||
|
О |
|
Q 6 в ЮЮг ТУ Рис. 10. Расчетная эффективная топлппровч і пості, (вг/и ■ град) А1203 в воздухе Экспсрн ментальные данные [197] для порпетост 1—42%. 2-51'" |
Ного или кристаллического вещества, обладают различными свойствами. Например, при прочих равных условиях тептопрс водность, а также модуль Юнга аморфных материалов пнж< . чем кристаллических. Очевидно, что это дает возможность регулировать свойства порошкообразных смесей, и вопрос о создании методики расчета таких смесей приобретает большое значение.
Нами предлагается схема расчета эффективной теплопр водности трехкомпопентпых систем, твердая фаза которых состоит из смесей двух порошкообразных материалов. Расчет состоит из двух ступеней. Вначале предполагается, что с _сь двух порошков представляет собой систему пулевой пористости. Эффективная теплопроводность такой системы рассчпты-
.1 "Ml
Эффективная теплопроводность порошков MgO и ЛІ..О, в воздухе,
И 10і н/лі"
|
Т. "К |
П |
ШІ/.Н- ■град |
К |
І Эксп |
^расч |
Формула |
І Эксп ^расч |
|
375 |
42 |
24,4 |
0,0318 |
0,433 |
0,425 |
(2.66) |
1,02 |
|
502,4 |
42 |
27,9 |
0,0387 |
0,502 |
0,515 |
(2.66) |
1,03 |
|
572,1 |
42 |
22,1 |
0,0450 |
0,552 |
0,556 |
( о2) |
0,99 |
|
723 |
42 |
110,0 |
0,0533 |
0,661 |
0,670 |
(2.52) |
0,98 |
|
810 |
42 |
13,0 |
0,0560 |
0,660 |
0,680 |
(2.52) |
0,98 |
|
343 |
36 |
2,0 |
0,0300 |
0,291 |
0,310 |
(2.52) |
0,94 |
|
430 |
36 |
2,0 |
0,0348 |
0,339 |
0,330 |
(2.52) |
1,01 |
|
825,7 |
36 |
2,1 |
0,051)0 |
0,493 |
0,610 |
(2.52) |
0 96 |
|
883 |
36 |
2,1 |
0,0615 |
0,523 |
0,540 |
(2.52) |
0,97 |
|
>373 |
12 |
30,2 |
0,031 Я |
0, 120 |
0,42Н |
(2.0b) |
0,98 |
|
373 |
42 |
22,1 |
0.0388 |
0,479 |
0,490 |
(2.52) |
0,97 |
|
1 673 |
■12 |
12,8 |
0,0505і 0,600 |
0,610 |
(2.52) |
0,98 |
|
|
873 |
4-: |
9,3 |
0,0615 |
0,695 |
0,720 |
(2.52) |
0,96 |
|
Материал MgO 1 О 268 мм ZrO., L 0,™>2мм i. o, (ІЗ |
И. ются по известным объемным соотношениям II геплопровод - постям компонентов. При соотношении теплопроводности компонентов I 200 эффективная теплопроводнотсь находится по соотношению Оделевского (2.43) или Максвелла — Эйкена (2.42).
Г-ели соотношение теплопроводпостеіі компонентов больше 1000. го для расчета используется формула Бру'ггм'ана (2.33).
Когда же отношения геплопроводпостеп компонентов твер - JH фа^ы лежат в области 200- 1000, величины, рассчитанные I прив денным выше соотношениям, усредняются.
'аес іита эффективную плопроводпость двухкомпонепт - пиіі вердоіі фазы и определив реальную пористость системы, можно папги эффективную теплопроводность системы с учетом третьего компонента. Расчет приводится по формуле ■ 2.52).
I.1 С 'і п ц.1 22
|
Xjp. lK'l српсгпк э |
11 і 1,1411 - I.1C |
Лі=о, |
|
Пористость порошка, "(, Объемный вес порошка, кг/м3 Плотность монолита, кс/м3 Обтеипые доли компонентов, "„ |
39 720 1180 50 |
7Г> 957 3800 50 |
|
Эффективная теплопроводность смеси порошков плексигласа и А1203 в воздухе, #=Ю5 н/м-
|
' В качестве примера приведем расчет эффективной теплопроводности смеси порошков плексигласа и безводной окиси алюминия в диапазоне температур 80—300 °К в воздушной среде. Частицы плексигласа имеют одинаковые размеры, рав - нле 60 мк. Частицы окиси алюминия — кристаллы неправильной формы, максимальный размер 60 мк. Другие исходные данные для расчета представлены в табл. 22. Результаты расчетов сведены в табл. 23.
График расчетной кривой представлен на рнс. II.
|
|
Pin - II. Эффективна» теплопроводность смеси ■ ротков плексигласа и А1203 в воз" H--HY- н/м1
Для проверки полученных расчетных данных было проьстс - но экспериментальное определение коэффициента эффективной теплопроводности казанного материала в том же диапазоне гем пера т р.
Сравнений1 расчетных и экспериментальных данных подтер даег во іМожпость расчета эффективной теплопроводпо - III тройной системы в ісівіїснмости от температуры.
Уіето і обобщенном проводимости весьма успешно применяйся п дтя расчета волокнистых систем с хаотическим расположением волокон (вата, войлок, стекловолокно) [230]. Особенностью таких систем является большая пористость 0,80—0,09. В работе [230] рассмагривасті теплопроводность
V Г
|
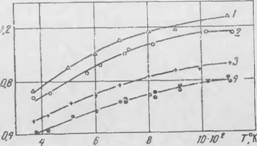
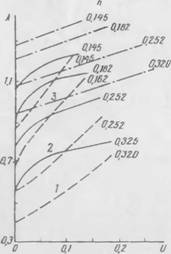
Г"'- - - |
Рис. 13 Зависимость >..,, і ті Ін-град ■текшвпты n іикуумс (rf -1.15 j.'/.ji) плотности у (кг/м3)
Экспериментальные д, мнімо; 2—расчішьіс по (Іюрмул. ім |230]
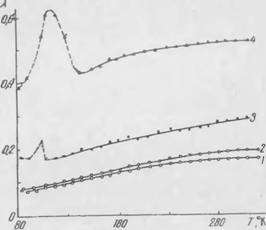
Стекловолокна, состоящая нз кондуктивпоп п лучистой проводимости. Поскольку вклад лучистой составляющей незначителен. то рассчитывается копдуктивпая_теплопроводпость.
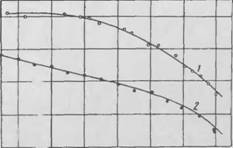
На рис. 12 и 13 показана зависимость лучистой теплопровод, стп?. , метім • град стекловаты в вакууме от диаметра
Стекловолокна сі (мкм) и от плотпости у. Рис. 14 позволяет сравнить экспериментальные данные н расчетные по формулам [230], удовлетворительное совпадение результатов подтверждает незначительность лучистой составляющей.
О возможности синтеза материала с наперед заданной теплопроводностью. Поставленную задачу можно рассматривать достаточно широко: скажем, как задачу, призванную обеспечить не только желаемую величину коэффициента теплопро-
|
|
|
0,06 |
|
О, а</ |
|
Рис. 14. Зависимость теплопроводности стекловаты Я (вт/м ■ град) в воздухе от пористости Р и плотности у (кг/м3): I. 2, 3 — экспериментальные данные (диаметр полокна равен соответственно 5 мкм. Зо мкм. '<■■ «іклі); 4, 5, 6—расчет [230]. с!=5.35. ІС4 и км соответственно |
|
QD2 |
Водности (разумеется, того порядка, каким могут обладать смеси различных порошков с различными газообразными пли жидкостными заполнителями), но и получить желаемый ход теплопроводности в заданном рабочем диапазоне температхр.
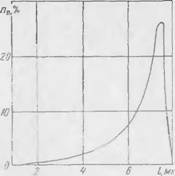
Эффективная теплопроводность порошков меняется в широких пределах уже в зависимости от теплопроводности исходного твердого вещества. Наряду с этим широкие возможности по регулированию теплопроводности гранулированных материалов и их смесей открываются потому, что перенос тепла в таких системах является сложным н определяется, как уде было сказано выше, эффективной теплопроводностью скелета смеси конвекцией (которую приходится учитывать, если размеры пор больше 5 мм), лучистым переносом тепла через поры, а также переносом тепла через само твердое вещество Параметрами, определяющими эффективный коэффициент теплопроводности в рассматриваемом случае, будут абсолютные значения и относительные соотношения теплопроводно- стей исходных компонентов, объемные доли компонентов (пористость), диаметры частиц и диаметр пор (от диаметров пор
в значительной мере зависит ход теплопроводности при высоких температурах), оптические свойства вещества, степень нолидиснерсностн частиц, поверхностные свойства частиц (наличие или отсутствие окисних пленок, степень мнкрошерохо - ватости частиц), форма частиц, степень уплотнения, внешняя нагрузка, величина модуля упругости твердого вещества и другие свойства (рис. 15).
Одним из способов регулирования величины эффективной
Теплопроводности порошкообразного материала является изменение давления либо химического состава газа-наполнителя.
Сели использовать в рабочем диапазоне 77- 300 °К коп-
Ц нснрутощиііся газ-паиоліппсль. например фреон-12, то кри - чффектнвной теплопроводности системы в рассматрнвае - пазоне температур будет более пологой (в сравнении < асм использования неконденсирующегося газа) вслед-
1 и фс вого превращения газа в жидкость, а затем в твер - Из-за незначительного объема образующейся жид - н сра •нительн неб тыного значения скрытой теплоты і. iiuuupa юі'шия обмен іспл'і в системе і точке фазового перехода может быть незаметен, а эффект приращения теплопроводности вследствие конденсации и іатвердевания газа в местах пятен касания частиц будет ощутимым. Структура об - р вавшейся твердой фазы (а также и теплопроводность) Чдет определяться скоростью охлаждения и в отдельных слу - во ідснсгвием внешних силовых нолей (акустических, магнитных и т. д)
Л порошкообразных материалов га іом-наполпіітелем га і дна особенность: происходит качественное изменение ар.-і т.-ра теплопроводности при умепынеинн размеров час - . і, . следовательно, п пор до величины, когда средняя длина ilium пробега молекул і а 1.1 сі. иіоппгої сон шсрпмоіі і - !еріПїім размером но|) (что аиа. чогпчпо ннюлиснню сре - ірі'жепніїїм г/кім) Это как рТГ; с. чхч. тн, когда эффек - игп кплопроводнос п. порошка может ок: ..тп. ся меньше
|
|
I ' и 1 1 піц - п| 1 .1
Основываясь на структурной схеме механизма теплопроводности порошкообразных материалов, можно подобрать такую смесь, свойства которой будут оптимальны в качестве теплоизолятора.
Известно, что лучшие типы вакуумно-порошковой изоляции А:„|,ф=20—30- 10~4 пт/м • град, используемые в ере іе с ра ipe - жепнем 10 1 н/м2 в температурном диапазоне 77- 300 °К и 20- 300 °К, изготавливаются па основе продуктов Si02 (перлит, кремпегель, аэрогель, белая сажа и т. д.), которые сравнительно дешевы, обладают высокой пористостью (80—96%) и малой теплопроводностью основы материала Лск в указанном диапазоне температур. Однако, как показали эксперименты, этот вид порошков является полупрозрачным для теплового излучения с длиной волны 4-—8 мк [243—248].
|
Ч |
Тепловой радиационный поток для системы радиационных экранов, параллельных наружным стенкам, можно найти по формуле
CAT __Л)
2 , 2п, , 14
—1------------------------------------------------------------------ (я + 1)
Где С — постоянная Стефана—Больцмана; ест коэффициент черноты стенок; еЭкР — коэффициент черноты экранов. Исходя из этой формулы, тепловой радиационный поток можно уменьшить как за счет увеличения числа экранов с низким коэффициентом черноты, так и за счет уменьшения коэффициента черноты стенок.
Тепловое излучение неметаллических порошков МОЖ1. уменьшить путем изменения коэффициента преломления нзл - чения (добавки других порошков [246]). В некоторых работах [246, 247] рекомендуется добавлять в эти порошки металлические частицы алюминия или меди, которые играют роль тепловых экранов. Так, например, в [246] показано, іто добавление частичек диаметром 40 мк в аэрогель (0 = 25 мк) уменьшает эффективную теплопроводность после uicro ~ вакууме с 22-10 4 до 8-^-10- Ю-4 втім - град, а добавление х. кчіьев последнего (0 = 0,5 мм) снижает эффективную теплопрішид ность с 22-Ю-4 до 13-Ю-4 втім-град в диапазоне темпера тур 77-f-300 °1.
Однако анализ факторов переноса тепла в вакумпровап - пых порошках говорит о том, что выбор металлических добавок алюминия или меди в перлит, аэрогель, кремпегель или белую сажу не является лучшим решением. Существует опре деленный оптимум, когда пзлучатсльиан способность металли чеекпх порошков близка к пзлучательиой способности боль
шн кусков данного металла, а контактная теплопроводность н порошке еще не очень велика. Однако этот оптимум для ме іаллпческих порошков очень узкий (200 -500 мм) [247]. Сле дует т кже отметить, что частички порошков из А1 и Си легко покрываются пленкой окиси при взаимодействии с кислородом, их коэффициент черноты увеличивается. Поэтому в настоящее время ведутся поиски новых добавок, существенно уменьшающих эффективную теплопроводность вакуумно-по - рошковоп изоляции
Твердые порпсіьіс системы. Применение метода обобщенном проводимости для исследования эффективной теплопроводности твердых пористых материалов рассмотрим па примере шамотноп керамики, материала, находящего особо широкое применение в технике в качестве огиеупора и тепловой и ляпни в широком температу рном диапазоне, для изготовления керамических фильтров, в условиях охлаждения транспи - гацпей п т. д.
Химический состав выбранной в качестпе объекта і ія пс - ii->Loii. iмті піамотпоп керамики следующий (п процентах по у ]: SiO, - 64,5%; A!2Os - 32,8%: KcsO:, -- 0,0%; ТЮ2 - 1," . CaO -0.6%. Так как примеси Fe20.;. Ті02 и СаО со - v гаплик і ие иачнтстьиу ю объемную долю, оказалось возмож - іьім ими пренебречь п рассма грішать гнерду ю основу (скелет) керамики кап двухфазную систему, состоящую из двуокиси кремния п окиси алюминия, приняв [219], что больший пи > ■!) і-.емч комп иеит образует непрерывную среду, в которой диспергированы частицы второй, меньшей по объему фазы. Определение температурной зависимости коэффициента теплопроводности этой двухфазной системы было проведено путем использования соотношения В. И Оделевского:
_________ Уаі,0,___________
____ 1_________ 1-уаі. о, '
1—/-ai2o,/^-sio. з
Полученного для расчета проводимости маїрнчпой двухфазном геїсрогепноп системы Под матричной понимается систе Ma которой одна фа.,а образует связную матрицу при Ліоном ее объемной концентрации. В пашем случае матрицей является Si02. Для расчета коэффициента теплопроводности келета керамики в широком диапазоне температур исобходп - ю :іц гь температурные шипснмостп коэффициентов геило - 'гронодпостн компонентов скелета. Со нггствуДшше данные ы 1 яты из рабо - [I, 175 249] для аморфного Si02 п из, ! 10'' 250] .ля крисіа. і.іпчегкші М П
Результаты расчета по соотношению В. II. Оделевского полностью совпадают с результатами, полученными при ис пользовании соотношения Максвелла Эйкена:
1 + 2oai, O,
|
|
1— ^siosAauo,
2Xsi0j/^AIj03 + I
Это подтверждает вывод, сделанный, в частности, в рабоїе [9] о хорошем согласовании результатов, полученных при расчете теплопроводности по этим формулам.
Следующим этапом расчета было определение эффективной теплопроводности керамики, так как шамотная керамика представляет собой материал с сообщающимися порами, было использовано соотношение Г. Н. Дульнева, полученное для определения теплопроводности двухкомпонептной дисперсной системы с сообщающимися порами [224]:
|
|
|
1-г(1 V, |
|
■ (2 67) |
При расчете по этому соотношению необходимо знать пористость материала, которая была определена экспериментально. Для этого предварительно взвешенный керамический образец помещался в вакуумную камеру, из которой откачивался воздух до вакуума 1 н/м2. После того как образец в течение двух суток находился в разреженной среде, сосуд с образцом заполнялся бензином. Повторное взвешивание образца позволило найти величину открытой пористости, которая оказалась равной 40%.
Расчеты, приведенные с использованием удельных весов и объемных соотношений компонентов керамики, показал і, что в материале имеется незначительное количество (около 5%) закрытых пор.
Анализ распределения пор по радиусам позволил определить преобладающий размер пор керамики, который был равен 2 5 мк.
|
|
Передача тепла в порах, так же как и в случае зернистых 1 материалов, может осуществляться посредством механизма молекулярной теплопроводности газа, конвекции и лучистого теплообмена. Для расчета молекулярной теплопроводности газа в порах материала использовалось обобщенное уравнение. Необходимость использования этого уравнения была ви |
Звана тем обстоятельством, что шамотная керамика представляла собой достаточно тонкопористий материал, в котором размер пор соизмерим с длиной свободного пробега молекул газа (величина критерия Кп порядка 10~2).
Для пор в 2 5 мк и небольших градиентов температуры эффектами конвективного переноса тепла в порах можно пренебречь [9]
Влияние излучения в порах материала было оценено при помощи соотношения [9]
X" 2 V-СТЧ.
Г
Расчет по этой формуле показал, что во всем температурном диапазоне исследования коэффициент лучистой теплопроводности з порах составляет величину не более 1,5% от величины коэффициента молекулярной теплопроводности.
Данные по температурным зависимостям коэффициента теплопроводности компонентов скелета керамики, газа, за полииющего ее поры расчетные значення температурных за ннснчостей, коэффициента теплопроводности скелета, а также эффективной теплопроводности шамотной кера-мпкн представлены в табл. 24.
-Экспериментальная часть работы была выполнена двумя методами. Исследования в диапазоне 80- 300 °К в вакууме и в среде различных газов (воздух, фреон-12, гелии) при атмосферном давлении были проведены па установке и методом, описанным в [174—178], (рис. 16- 18) Исследования в диапазоне температур 400—1200 °К в воздухе при атмосферном давлении проведены методом и па установке описанными в [181. 182].
Расчетные и экспериментальные величины достаточно хорошо согласуются. Расхождения лежат в пределах 10% Тот факт, что экспериментальные значения лежат несколько ниже расчетных, можно объяснить тем, что в керамике имеется пе - ч 1 количество закрытых пор. Следует отлієтить также, что вши ;і, шее расхождение расчетных величии с экспериментальными данными характерно для фреопа-12, т. е. газа, длина свободного пробега молекул которого (Л=0.024 • 10~6 м) меньше, чем у воздуха (А = 0,06- 10 6 м) и тем более у гелия ( 0,2- 10 6 м) Йч работы [231] можно предположить для фреопа-12 и в некоторой степени для воздуха наличие в ке - раміг е направленного потока газа вследствие градиента давления, во шикающего под действием градиента температуры, что и вызывает понижение коэффициента эффективной тепло - провоіности керамики в атмосфере этих газов.
Н. І пне. 19 приведены кривые температурной зависимости ■ • «|иі>іііш<чігоіі теплопроводности компонентов скелета кера-
|
Расчетные и экспериментальные величины коэффициента эффективной теплопроводности пористой шамотной керамики в функции от температуры
0.81 0 85 |
0,51 0,71 0,80 0,86 0.96 1,03 1,13 1,32 1 .">7
Ыики и скелета в целом, расчетная кривая коэффициента - ф- фектииной теплопроводности керамики в воздухе при атмосферном давлении н экспериментальные данные (точки).
|
300 |
32,5 |
1,28 |
2,85 |
— |
0,90 |
|
400 |
23,5 |
1,50 |
3,11 |
— |
1,02 J |
|
Воздух, И 0,133 |
Остановимся еще па одном существенном и интересном обстоятельстве, которое вытекает из анализа соотношения (2.20). Очевп шо, что если экспериментально определить величину ЛЭфф материала, например, в воздухе, то, зная пористость этого материала, из соотношения (2.20) можно найти теп то проводиость его скелета. Зная же ЯСк и теплопроводность ка кого-либо другого газа, можно, использовав его соотношение, рассчитать X™i„j, в атмосфере этого газа Следует сказать, что большинство функционирующей аппаратуры для опретелення
Теплофнзнчееких характеристик материалов а температурном диапазоне 400—1200°К не предусматривает наличия вакуум - поп системы, следовательно, на данных установках нельзя проводить исследования в различных газообразных средах. Поэтому такого рода расчеты могут значительно расширить исследования тепловых свойств пористых; материалов, используемых в атмосферах, отличных от воздушной. Более
Того, если дополнительно известна,, температурная зависимость теплоемкости материала или коэффициента его эффективной температуропроводности в воздуїннон среде, то появ - лжм ч возможность рассчитать температуропроводность по-
|
Ристого материала в атмосфере различных газов. Другими словами, найдя экспериментально температурные зависимости коэффициентов эффективной теплопроводности и температуропроводности (или теплоемкости) в воздушной среде и зная пористость, можно рассчитать температурную зависимость
Рис 18. оЭфф (вт/м-їрад) шамотной керамики в различных газовых средах: /—гелий 2—воздух; 3—фреон-12 (при Н— І05 н/л!). 4 воздух (//=»!—10 н'м 1 |
|
|
Проведенные эксперименты и расчеты подтвердили высказанные положения. На рис. 20 приведены расчетные кривые температурных зависимостей коэффициентов эффективной температуро - н теплопроводности шамотной керамики в атмосфере гелия, определенные па основании экспериментов в воздушной среде. Эти кривые удовлетворительно дополняются экспернмептальпы. мн точками, полученными в результате исследования теплофнзпческих характеристик шамотной керамики в атмосфере гелия в температурном диапазоне 80—400 °К [181, 182]
Рік-. 20. it-п о [in ментальные и рлс - чіпчіьіі шачепнй коэффициентов эффективной температуро - {м/ик) п тен попроси чпостм (ог/ и • град) ничотіюіі керамики и пищухе (/ н 2— эксперимент [176])
Влажные пористые системы. Особый интерес представляет экспериментальное исследование теплопроводности трехфазных пористых систем, так как эти системы состоят из трех фаз, а именно: пористого тела —скелета, газа и жидкости в порах, причем количество жидкости в порах (и влагосодержание) изменяется в пределах 0<L,<100%, так как при U=0 или U= = 100% будет двухфазная пористая система. Вследствие по - ьерчносі пых явлении смачиваемая жидкость обволакивает пленкой частицы пористого тела, и благодаря действию капиллярных сил наиболее вероятными местами концентрации жидкости яваяются области, примыкающие к стыку частин друг с другом. При этом жидкость, которая образует пленку, проявляет свойства, отличные от свободной жидкости, и называется связанной. Экспериментально были сняты температурные зависимости теплопроводности кварцевого песка (</ = 0,5 мм, //=.!()%) при следующих влажностях (t/=*543, £/ = 0,162%), і'оторьіс показаны та рнс. 21. а {янмыс для?«;,фф приведены в іабл. 25, 26. Как видно из графиков зависимости рис. 21, даже небольшое увеличение влажности вызывает заметное увеличение эффективной теплопроводности. Кроме того, при темпера - IV pax 123 °К II 273°К заметны зоны-фазовых переходов. Оче - гндно. н точке с температурой 123 °К фазовый переход обязан спя иной воде, а в точке 273 °К - обычной вотс. Теоретические исследования эффективной теплопроводности трехфазной
пористой срсды были проведены в работе [242], авторы которой распространили на трехфазную систему основные положения, выдвинутые Вудсайдом и Месмером для двухфазной системы. Показано, что параллельное распределение составляющих фаз относительно теплового потока дает максимальную эффективную теплопроводность, выражающуюся в этом случае через среднее арифметическое значение теплопроводностен двух фаз, в то время как перпендикулярное распределение со-
А 0.1
|
|
Сгавлиюшпх фаз относительно теплового потока дает минимальную эффективную теплопроводность, выражающуюся в этом случае через аналогичное гармоническое значение тспло - проводностеіі, твердого тела и жидкости. В случае реальной псристоіі системы эффективная теплопроводность лежит между указанными случаями и выражается как среднее геометрическое теплопроводностен двух фаз.
Для случая, когда три фазы расположены параллельно направлению теплового потока, эффективная теплопроводность образца определяется следующим выражением:
Лэфф - UK + (Я - U) хпар -(- (I - П)
Где /.ж - теплопроводность жидкости; — теплопроводность материала скелета пористой системы; Л„ар теплопроводноегь паров в воздухе; U — влажность (влагосодержанне по обь - ему); П — пористость
Т а б л її ц а 20
Эффективная теплопроводность кварцевого песка при влажности U 0,543%
![]()
|
91 |
5 |
|
102 |
4,5 |
|
113 |
3,23 |
|
123 |
2,89 |
|
142 |
4,02 |
|
162 |
3,84 |
|
182 |
3,82 |
|
199 |
3,69 |
|
216 |
3,39 |
|
232 |
3,35 |
|
250 |
3,54 |
|
259 |
3,03 |
|
264 |
2,95 |
|
270 |
2,81 |
|
273 |
2,37 |
|
276 |
2,84 |
|
178 ■ |
3,11 |
|
284 |
3,85 |
|
293 |
3.42 |
|
295 |
3,48 |
|
301 |
3,13 |
|
319 |
3,52 |
|
339 |
3,03 |
|
346 |
3,13 |
|
2,73 2,58 2,50 3,06 3,28 3,78 3,94 3,77 3,58 3,58 3,22 3,18 3,10 3,08 3,08 3,08 3,08 3,46 3,46 3,46 3,46 3,46 2,76 2.76 |
|
0,207 0,218 0,294 0,4025 0,375 0,374 0,392 0,388 0,401 0,407 0,346 0,397 0,401 0,418 0,495 0,412 0,376 0,341 0,384 0,378 0,42 0,374 0,34 0,335 |
|
0,0412 0,0342 0,0269 0,0271 0,0387 0,0294 0,0339 0,0275 0,0232 0,0192 0.0188 0,018 0,0184 0,0175 0,01395 0,0161 0,01.% 0,0216 0.0184 0,017 0,01075 0.0172 0,0135 "0,013 |
Когда же гри фазы расположены перпендикулярно направ ленто теплового потока, эффективная теплопроводность трехфазной системы определяется соотношением
ж пар Лск /
Эффективная теплопроводность для реальной трехфазной системы определяется выражением
Кфф-КЧ1-П)Ч^-и)- (2.69)
Если П=и (т е. полное насыщение водой) или U=0 (т. е. насыщение воздухом), уравнения (2.67—2.69) подобны уравнениям Вудсаїїда и Мессмера (1961 г.), полученным для двух фазной системы
В работе [242] предложено следующее соотношение для трехфазной системы, выведенное при использовании принципа обобщенной проводимости:
*зфф = П) + Лпар (Я - U) ЗХСК/(2ХС1. 4- ?.пар)
+ XmU3XCK/(2XCK + XJ] [(1-Я) + (Я-U) ЗХСК(2лск - - Лпар)
+ U3XCJ(2XCV Хт)Г1- (2.70)
Эффективная теплопроводность известковых песков при различных влажностях для фиксированных значений пористости (Я) была подсчитана по формулам (2.69 и 2.70), при этом использованы данные (1961 г.) для >.,к. Хек. >.„.,p (лСк= = 1,6 ккал/м ■ град ■ сек, ЯПаР = 0,0237 ккал/м ■ град • сек, /ок = =0,545 ккал/м-град-сек). На рис. 22 показаны рассчитанные значения для лэфф вышеуказанных систем, а также и экспериментальные данные, полученные авторами.
При сравнении теоретических и экспериментальных данных можно заметить, что расчетные данные для лэфф по (2.69) не согласуются с экспериментом, особенно вблизи области насыщения, эти несовпадения объясняются неучитыванпем структуры и распределением фаз в среде.
|
81 |
Уравнение (2.70) было получено для системы сферических частиц, и при рассмотрении известковых песков можно полагать, что составляющие фазы имеют сферическую форму Расхождения между теоретическими данными, полученными из (2.70), не являются неожиданностью, так как в [242] применяется модель к пористым трехфазным системам птем до лущения, что некоторая часть известкового песка включает твердое тело как непрерывную среду и жидкость, как диспергированную в пей, тогда с этой точки зрения образец состоит из
Li :.1к Пмі
Частичного водонасыщенного компонента с остатками в форме изолированных пакетов, недоступных для воды.
Используя это допущение, вышеуказанные авторы обнаружили совпадения между расчетными и экспериментальными значениями. Но в частично насыщенном образце степень непрерывности трех фаз играет важную роль в оценке теплопроводности, поэтому форму ла (2.70) неприменима.
Интересно рассмотреть выражение, аналогичное уравнению (2.09), полученное введением максимального (2.07) п
|
Рис. 22. Теплопроводность К (кка. іім ■грид ■ сек) и. шсс гкоиого песка в зависимости от влажности U для различного значення пористости: |
|
|
|
П 090 0.85 О. вг 078 |
|
Рис. 23. Значения коэффициента п для влажностеи U и пористости П |
|
О.' |
|
02 U |
По (2.69); 2—эксперимент-, рлечет по (2 70)
Минимального (2.68) значений >к.„|„|„ в какоіі-то степени учитывающей весовой фактор распределения различных фаз в образце
Так, если п — количество фракции (весовая доля) в образце, расположенных так, как учитывалось при выводе уравнения (2.67) (1 —и), соответственно в уравнении (2.68), тогда уравнение будет иметь вид
1 - П У 1—11 ,»фф эфф! I эффТ-
(2.71)
|
І—р. ісч |
На рис 23 показана зависимость Хот U при фиксированной норне гости (Г!) Отмстим, что VIя фиксированной пористости
в области 0,145 до 0,326 экстремальное значение находится между 0,9 и 0,8. Это показывает, что распределение фаз в естественном образце такое, как предполагалось при выводе (2.67), фазы расположены параллельно направлению теплового потока. Но применять (2.71) можно только в том случае, если есть экспериментальные значения для?.эфф трехфазной системы, так как п находится методом расчета по эксперммен тальным данным и значениями, подсчитанными по уравнению (2.71) при определенном п.
Можно сказать, что расчетные данные для лЭфф пористых систем (как двухфазных, так и трехфазных), полученных по формулам (2.69—2.70), не согласуются с экспериментальными данными для Я. Пфф этих же систем, так как в основном эти формулы выведены на допущениях, далеких от реальных систем.
Таким образом, необходимо проводить дальнейшие экспериментальные исследования тепловых свойств многокомпонентных капнллярнопорнстых систем для выявления основных составляющих механизмов теплопроводности, присущих этим системам, их взаимного влияния друг на друга, их зависимо сти от таких факторов, как температура, влагосодержание, пористость, процентного содержания компонент, размера частиц и их форм.
Большой интерес представляют исследования теплофнзи - ■ческих свойств зернистых материалов в средах различных газовых смесей. Пористые материалы могут использоваться как фильтры для разделения газовых смесей, при этом их теплопроводность играет существенную роль, так как разделение газовых смесей происходит тем эффективнее, чем выше перепад температур на поверхности пористого материала.
Рассмотрение методики расчета эффективной теплопроводности указанных выше систем необходимо проводить при наличии следующих допущений: объемная концентрация скелета равна плотности абсолютно сухого тела, скелет является лно - фильным, вещество в виде жидкости находится в физико-механической связи со скелетом, перенос вещества в порах может осуществляться только диффузией или эффузией. Скелет может быть как в виде твердого пористого вещества, так и в виде порошкообразного или смеси порошкообразных материалов, но без химического взаимодействия друг с другом.
Рассмотрим пористые среды при полном заполнении пор веществом (жидкость, газ, лед) и при заполнении пор только паром (капиллярная влага и адсорбционные пленки составляют незначительную часть объема пор) в смеси с газом (воздух или другой инертный газ).
Масса воздуха и пара в порах при незначительных отличиях давления от барометрического ничтожно мала по сравнению с массой жидкости или льда (около 10~5% от массы жнд-
kdctii, соответствующей равновесному влагосочержаппю), т. е. можно принять, что в обоих случаях содержание вещества в порах равно содержанию жидкости или льда.
Выше было показано, что эффективную теплопроводность сухой пористой системы (в порах сухой газ) можно выразить как функцию ряда параметров, таких, как пористость, эффективная теплопроводность скелета, теплопроводность газа в порах, давление газа, температура, механическая нагрузка на материал, состояние поверхности скелета (частиц для порошкообразных материалов), геометрических размеров частиц, их оптических характеристик и т. д.
Рассмотрим герметичную систему, поры которой заполнены жидкостью или льдом - Для такой системы в работе [248] приведена следующая система дифференциальных уравнений массо - и теплопереноса:
Дт () Г
KiA - Т I - и,
От
Где коэффициенты А?„, kvl,
/?22» Кл| при использовании мстодя зонального расчета можно принять постоянными и равными: для системы жидкость—пар
= am = aml + amZ> k<L = aJn = Gm6.
Ku aTm — = а,„,б r'2 , k2i =
|
Ml |
С с с
Для системы лед—пар
Ku oml, kxi а7
*si = аи, і — , а + аТ ^ .
С с
Здесь и — общее влагосодержаппс тела, Т — температура; а - коэффициент диффузии влаги (пара и жидкости) во влажном геле; я,„,— коэффициент диффузии парообразной влаги во влажном теле; аш2 — коэффициент диффузии жидко - образной влаги во влажном теле; а7. , и7., соответственно
1 ПІ I * /НІ
Коэффициенты термодиффузнн пара и жидкости во влажном теле: о коэффициент температуропроводности; с — удельная теплоемкость; г — дельная теплота фазового превращения. г - термоградиеитиып коэффициент.
І
Пусть поры полностью заполнены жидкостью, тогда тепловой поток в данной системе
Q = - [X + (Л— /„) t = — ХтЛі,
Где Л8І(В—эквивалентный коэффициент теплопроводности, равный
А*™ = * [ І + (Л - Л.) ] = М і +
/ — источник; у0— плотность абсолютно сухого тела.
Для приведенного выше случая £ = 0, поскольку при больших концентрациях жидкости термоградиентный коэффициент 5 = 0. Таким образом, в данном случае эквивалентный коэффициент теплопроводности вещества в порах равен его истинному коэффициенту. Следовательно, описанное выше модельное представление переноса тепла в пористой системе можно использовать и в данном случае, а также для случая, когда в порах находится лед при отсутствии фазового перехода.
Расчет эффективной теплопроводности таких систем можно вести по формуле (2.52). Для твердых пористых систем /1=0.
С целью проверки применимости формулы (2.52) для рас чета эффективной теплопроводности влажных пористых систем были проведены эксперименты с зернистыми и порошкообразными материалами при заполнении пор различными жидкостями (рис. 24, 25). В качестве объектов исследования были выбраны системы: стеклянные шарики в воде, этиловом спирте, бензоле, кварцевый песок, вода, а также смесь порошков плексигласа и Л12Оз, кремнеорганнческая жидкость ВКЖ-94. Результаты экспериментов и расчетные величины Хэфф представлены в табл. 27.
, Рассмотрим случай, когда в порах вместо сухого газа ил л жидкости находится бинарная газовая смесь газ — пары какой-то жидкости (например, воздух — водяные пары). Сделаем следующее допущение: жидкость внутри пористого тела находится в виде адсорбционных пленок, пара и отдельных капель сконденсированной влаги, т. е. содержание жидкости не превышает величины <[м, при которой пренебрежимо мала ненасыщенная гидравлическая проводимость k в формуле Дарен
І —
Где Ф и у — соответственно потенциал и плотность жидкости
|
|
Для таких систем перепое массы под действием градиента температур происходит в основном в виде переноса пара. Если Ііфіи, то градиент влажности в пористой среде вызывает обратный поток жидкости. При малых концентрациях жидко сти обратные потоки ее мало влияют на /.„[„|Р. Если лпм влиянием пренебречь, то мнимую теплопроводность бинарной л
0,6
Г у,
|
|
|
180 |
|
280 |
|
02 |
|
80 |
|
|
|
I'm 2-І 1Ч'іі. ііііі)м>іі(>лііоі'іі> глажін. іч м. інрп (вг/м - град); / порошкообразный плексиглас; 2—порошок А1;Оэ лух; 3—кремнеорганнчсская жидкость: 4—порошок кре М Ііічіргл IIII Iicctd Я ЖIIДКОСТ1» |
|
— воз- HLO.,— |
|
Рит. 25. Теплопроводность влажных материалов (вт/м-град): — / стеклянные шарики d—1.5 мм—воздух; 2—стеклянные шарики d=0.5 «и — воздух: 3—стеклянные шарики d = "2.0 мм—пленка крем неорганической жидкости; 4—стск- і'.'іиімс шарики rf = 2.fi M. v кремиоорглничегк. ш і£імкснчі» |
1,'llM
|
Эффективная теплопроводность влажных систем Г = 300 °К, Н = 0,99-105 н/л2
|
|
Газовой смеси газ виде [192] |
|
Н„ |
|
DT |
Пары жидкости можно представить в Нп 1 dH„
Хэфф = LD
Где L — теплота фазового перехода; D — коэффициент диффузии; Нп — барометрическое давление в системе; Нг — пар циальное давление водяного пара; - у — плотность водяного пара, Hvs — парциальное давление насыщенного водяного пара. Давление пара Hv можно представить в виде
Где ср — относительная влажность смеси газ — пары.
При равновесии между жидкостью и паром в порах с[ находится в следующей зависимости от давления столба жидкости;
Ф= exp (Mg<t>/RT),
Где М — молекулярный вес; g — ускорение силы тяжести; Ф — потенциал жидкости.
Когда влажность смеси газ—пары жидкости меньше мак спмальной гигроскопической влажности, ее можно определить
но изотермам сорбции. Численные значення при ц I
Представлены па рнс. 2G. Экспериментальные данные представлены на рис. 27—29.
Следует остановиться па некоторых особенностях расчета влажных пористых систем табл. 28. При определенных cooi-
|
При молекулярном переносе вещества в виде пара пото., п| порциопалеп градиенту парциального давлення пара, чае іффузпонпого переноса градиенту величин, і Н | Т Так кгік на ( іьіке частиц геометрнчеекпе размерь! чнкр Че| ховатостеі'і. как правило, составляют 10 2—10~ ч ра0 часгпц, то іля реальных зернистых материалов типа пес даже при нормальном барометрическом давлеипп бу j пли место эффузиопнын механизм переноса массы. Благодаря действию капиллярных сил наиболее вероят ми месіамн концентрации жидкости являются области, при |
0,5 ношениях между парциальными давлениями газа и парт, длиной свободного пробега молекул газа и пара, а также геометрическими размерами пор и мнкрошероховатостей н стыке частиц перенос вещества может происходить как в впте диффузии, так и в виде киудсеповского течения (эффузии).
|
Сравнение расчетных и экспериментальных коэффициентоп теплопроводности влажного кварцевого ческа
|
Мыкающие к стыку частиц друг с другом. Таким образом, г» области мнкрошероховатостей наиболее вероятным сосгояин м является наличие пузырьков смеси газ — пары, изолированных от больших пор пленками жидкости. Процесс испарения — конденсация в микрошероховатостях будет иным по ч равнению с испарением и конденсацией в больших порах Дл Карцевых песков при температуре выше.500 °1 температурные градиенты на стыках между частицами недостаточны для конденсации водяного пара, в то время как в больших порах эффект испарение — конденсация имеет место. В таких случаях расчет эффективной теплопроводности нужно проводить с учетом различных механизмов переноса вещества в порах и микрозазорах.
Теплофизические свойства полимерных материалов. Прн рассмотрении тепловых свойств теплоизоляционных материалов нельзя не остановиться на характеристиках полимерных материалов, которые в настоящее время имеют самое широкое распространение. Армированные пластины и смолы обладают рядом весьма ценных свойств. В аблирующих материалах волокна повышают и усиливают сопротивление эрозии.
Кроме того, существует особая группа электропроводящих синтетических полимерных материалов [205]. Для наполнения используются электропроводящие материалы: сажа, графит и металлические мелкодисперсные порошки.
Интересные свойства были обнаружены при исследовании полистирола, в состав которого введено 5—10% алюминиевой пудры Оказалось, что стержни, изготовленные из такого материала, хорошо проводят переменный ток, оставаясь изоляторами для постоянного тока.
Теплофизические свойства полимерных материалов сильно івп' чг от температуры старении материала, его природы г|пкгры и свойств [270].
Современные представлении о надмолекулярной структуре по'Шмсрпых тел. Основные свойства ни ікпмо. іекулярньїх веществ в конденсированном состоянии всегда зависят пе только от состава и строения молекул, но и от их взаимного расположения, т. е. от структуры тела. Наиболее очевидным и широко известным примером такой зависимости является фазовое превращение (плавление, кристаллизация, переход из одной кристаллической формы в другую), при котором изменение всего комплекса физических свойств обусловлено хаотичностью. Молекулы всегда взаимодействуют между собой и поэтому располагаются с учетолі положения соседних молекул. Следовательно, в жидкостях существует так называемый ближний порядок, т. е. известная упорядоченность близко расположенных друг к другу молекул при полном отсутствии связи в расположении достаточно далеких молекул. При этом понятия «близко» и «далеко» понимаются в смысле соотношения с размерами молекул.
При кристаллизации возникает дальний порядок, т е такая упорядоченность молекул или атомов, когда их взаимные расположения пе случайны даже при сколь угодно большом удалении друг от друга.
Изучение упорядочения расположения макромолекул в полимерах на протяжении многих лет практически сводилось лишь к исследованию типа кристаллической решетки в случас кристаллизующихся полимеров и к определению ориентации макромолекул в случае ориентированных аморфных полимерных тел. Более глубокое исследование структуры полимерных тел не производилось.
Первые представления о структуре полимеров сложились после того, как было обнаружено, что эти вещества состоят из очень длинных цепных молекул.
Казалось совершенно очевидным, что образование регулярных структур подобно тому, как они строятся в случае малых молекул, совершенно невозможно, ибо размеры и форма макромолекул полимеров различны. Столь же очевидным казалось и предположение о том, что такие очень длинные и гибкие макромолекулы хаотически перепутаны между собор подобно нитям в войлоке.
Постепенно понятия упорядочения и кристаллизации отождествлялись, п кристаллизация стала рассматриваться как единственный источник порядка в расположении макромолекул полимерных веществ, а за меру упорядоченности принималась степень кристалличности. Эти представления никогда не были строго доказаны и устойчивость их в литературе связана, по-видимому, с простотой и кажущейся очевп і - постыо.
Основное предположение о невозможности образования ьысокооргпнп шваппых структур из больших молекул разлш IIOKI р,1 (Мера и формы было опровергнуто открытием едппич пых мпкрокристаллов высокомолекулярных соедипепнГі, обладающих геометрически правильной формой и внутренней структурой, приближающейся по своему совершенству к структуре кристаллов обычных органических веществ [205, 270J. Механизм ноншкповсипн таких структур в полимерах должен был быть совершенно иным, чем в ппзкомолекулярпых соединениях. Вскоре было найдено, что процессы кристаллизации полимеров могут происходить только в уже заранее упорядоченных системах и что простейшие явлення упорядочения макромолекул, т. е. возникновение падмолекуляр шх структур происходит уже в аморфных полимерах.
Агрегация отдельных пачек может приводить к ярко выраженным высшим структурам дендритного характера в случае стеклообразных полимерных тел и к структурам типа полосатых в случае высокоэластнчпых. Поэтому, строго говоря, іморфпьіх полимеров, т. j полностью неупорядоченных систем - lib'"- мысле ЭТОГи понятия, не существует, и точнее было. .і..чіоріпь о некристаллических полимерах
При. рисі і їли іацпп нр. тіімі'р. т пачечппп і труктурі. і спач. і ла происходи і фазовое превращение первою рода в пределах пачек образованней кристаллических лепт, а в многостадийном процессе дальнейшего упорядочения закристаллизованных пачек обра у ются высшие кристаллические надмолекулярные с грукт ры.
Кристаллизация полимеров п особенно возникновение таких высокоупорядочеппых структур, как единичные кристаллы, является лишь заключительным этапом процесса упорядочения, начинающегося в аморфном состоянии.
Исследование свопств надмолекулярных структур в '•лорфпом состоянии должно быть первым этапом неелсдова - 1ня полимеров с различными структурами независимо от того, способен данный полимер кристаллизоваться или нет.
В настоящее время доказано, что взаимное расположение цепей определяет все механические характеристики волокон, пленок, каучуков, пластических масс, и задача получения полимерных материалов с заданными свойствами в очень сильной степени зависит от структуры, которая придается материалу в технологических процессах. В то же время достаточно полных исследований влияния падмолекупярной струк - |ры па геплофп. шческне свойства (в частности, па теплопро - мо '.иость) полимеров и полимерных композитні до сих пор предпринималось.
Теплопередача в аморфных полимерах. По Дебаю тслпота г-ердьг т$лач передастся посредством упругих волн (часто ч н. алют звуковыми волнами). Волны рассеиваются па пс - чд ию' іях тверлого тела п теряют пз-за этого па своем ппш-еф.. Рассеивание фопопов ншепг от погреш - кости в строении решетки и от статистических термических отклонении плот пости. У правильно построенных кристаллов величина погрешности строения невелика, так что термическое расдгивапне играет решающую роль, и свободная длина упругой в. тлпы значительно зависит от температуры (закон Эи - кена).
В аморфных материалах, наоборот, погрешности в строении решетки должны преобладать так сильно, что термическими колебаниями плотности можно пренебречь. Поэтому свободная длина упругой волны как зависящая от температуры установлена Дебаем приблизительно.
Кнттель показал, что свободная длина упругой волны у аморфного силикатного стекла находится в пределах порядка величин междуатомных расстояний [271].
Принимаем, что у аморфного вещества радиус действия упругих волн равен расстоянию между двумя соседними атомами. Феноменологическая теория описывает передачу теп іа при помощи уравнения
Q —Л./*" ї^гіігі "7".
Для случая постоянной Я. в стационарном состоянии тепловой поток через поперечное сечение F
Если Д/' является приращением температуры на участке измерения D.
В аморфных веществах приблизительно каждому отдельному междуатомному расстоянию можно приписать элементарное тепловое сопротивление. Таким образом, аморфное тело с грубым приближением можно принять за решетку, состоящую из элементарных тепловых сопротивлении, причем отдельные атомы представляют собой узлы решетки, а элементарные сопротивления могут быть описаны через вполне определенные параметры отдельной связи.
Для этого в распоряжении имеются следующие величины масса и междуатомные расстояния, потенциал химической связи между соседними атомами или силы упругости упругих колебании вокруг положения равновесия и, наконец, вклад атома в поглощение энергии, т. е. в теплоемкость системы
Аморфные вещества с грубым приближением можно представить как имеющие прямоугольную решетку. Элементарное тепловое сопротивление междуатом його расстояния можно выразить через элементарную теплопроводность
|
|
Теплопроводность Яэ выражаем как
Где с" — теплоемкость, р — плотность. // —- скорость упругих волн, I ■— свободная длина упругой волны, — число в порядке величии больших единицы Гели взять весь спектр упругих волн, то
І
Элементарная теплопроводность уменьшается с увеличением массы атома и увеличивается с ростом постоянной упругости силы связи. Поэтому, например, основной валентной т-вязн можно будет придать высокую, а связи Ван дер Вааль са низкую элементарную теплопроводность При этом следует иметь в виду два сорта по существу различных тепловых сопротивлений: внутримолекулярные основные валентпостн и межмолекулярпые силы Ван пер Ваалы, і У полимеров игра юг роль, помимо этого, и силы Ban дер Ваальса между побочными группами.
Аморфные полимеры состоят из цепных молекул, ПОЭТОМ} их можно представить в виде решетки из основной валентно стп вдоль цепей и связей Ван дер Ваальса между цепями Основные валентные связи можно заменить низкими тепловыми сопротивлениями, а связи Ван дер Ваальса — высокими тепловыми сопротивлениями. Таким образом, получаем упрощенную решетку из двух видов тепловых сопротивлений. Приближенно можно принять тепловые сопротивления основных валентных связей как «ничтожно малые, т. е ко роткоза минутые п цепи.
В аморфных полимерах с гибкой полимерной цепыо молекулы имеют вид клубков, «глобул». В полимерах с жесткой полимерной цепью молекулы объединяются в пачкообразные свернутые надмолекулярные образования, и поэтому теплопередача вдоль основной валентной связи сильно затруднена. Теплопроводность всей пространственной решетки, т. с. морфінні полимерной пробы, можно считать пропорцпопаль-
I ой элемепгарной теплопроводности связи Ван дер Ваальса.
Генлонередача в кристаллических полимерах. Теплопро - ! і міосіь частично Кристаллизованных полимеров может оьіті представлена как состоящая из теплопроводности аморфной и кристаллической фаз. При - лом теплопроводность аморфної:
Л,,Ш НМСЄТ ТНППЧПуЮ ТеМІКраТуріїуЮ—WBIICHMOCTl» для полно стью морфпого полимера. Исходя из поведения геплопровод-
II. рпстал. шческой фа ш, частично кристаллизованные п і I u p.1 ■rtPVT быть НОДрл :1глепы НЛ Illi ' pMIIIU
В первой группе теплопроводность кристаллической фазы падает обратно пропорционально абсолютной температуре и тем самым следует закону для «простых» ппзкомолекулярпых кристаллов [271].
В другой группе теплопроводность кристаллической фазы увеличивается с повышением температуры как у нпзкомолеку - лярпых кристаллов сложного строения. В этом случае затухание упругих волн тем сильнее, чем «сложнее» строение спектра колебаний.
У кристаллов с очень сложным строением спектра колебаний затухание упругих волн таково, что средняя длина свободного пробега фопонов приблизительно равняется расстоянию между атомами. Таким образом, между такими крпсга і лами и аморфными материалами едва ли имеются различия относительно свободной длины пробега. Следовательно, при нятое для объяснения теплопереноса в аморфных полимерах представление о пространственной решетке из элементарных тепловых сопротивлений должно быть действительно и для кристаллических полимеров со «сложным» строением криста і ла. Этим и можно объяснить одинаковую температурную зависимость теплопроводности как у аморфных, так и у подобного типа кристаллических полимеров.
Экспериментальное исследование тепловых свойств некоторых полимерных материалов. В работе [164] рассматрнва ется температурная зависимость теплоемкости кристалличе ских и аморфных полимеров.
На рис. 30 показана температурная зависимость теплоемкости полиэтилена (кристаллический полимер). Оказывается, что теплоемкость его мало изменяется после закаливания при температурах ниже 20 °С, но зависит от способа изготовления образца. При нагревании полиэтилена от комнатной темпера туры степень кристалличности его падает, что свидетельствует о разрушении структуры, сопровождающемся поглощением дополнительного количества тепла и увеличением теплоемкости. Этим, вероятно, и объясняется более резкий рост теплоемкости при температурах выше 20 °С.
Структура н свойства полиэтилена изменяются с течением времени, это подтверждается наличием локального максимума па кривой теплоемкости (рис. 31). Резкие пики подтверждают изменение кристаллической структуры полимера при опречс - лснпой температуре, определяя зону стеклования (нппппласт па рис. 31 имеет зону стеклования при 77—78 °С).
К аморфным полимерам относятся полистирол, литьевой полптетилметакрнлат, органическое стекло, полпшшнлтолуол и т. д.
Образцы аморфных полимеров требуют тепловой обработки ц, чя снятия напряжений, возникших при прессовании п
изготовлении крупки полимера. Как ші шо пз рпс. 32—34, теплоемкость аморфных полимеров в большинстве случаев монотонно возрастает с повышением температуры. Солее рез - кіііі польем кривых наблюдается в области температур сгекло La мня.
На рпс. 34 наблюдается небольшой максимум в области стеклования п более высокое значение теплоемкости выше температуры стеклования.
' ii > и. ii і с,1 l. rf'l. j i, с 1.1 к ієііпі1го при 73° и смири - П ) п і

|
С 0.9 |
|
V-ШО ~80 - го О 23 ВО |
|
Рік ill Темпера ірили ншсіі - мость теплоемкости полінні іе ион (ка. і/г - г/ыд) : |
|
[О |
|
0.6 |
ІКЛЛОІІ. ІПГО при 7.г 11 си lip I с (п. 5CHI); 4 ПЭ н. н npuccoitaiiuoro; то же медленно охлажден югп, i. i ч'ік t - со тветствуст чедтеппо o^ м - .. ic'iioMv Пс) и п.) |IG-I] / іішінгегр. іі|ііор л плен. 2— ншшнллег;
|
|
|
05 |
|
°'-!00 -60 20 О 20 60 Г С |
|
Риг. ЗІ. Температурная іапнсп - мость теплоемкости (кал/г ■ град): |
I |ШЛН»111Л<-1| НИ ІКОН І1.10ГІІ0СІН I. IKJ ленного Н|Н1 .'>Г1 ' ( -] Іишгореіше ОІІ1.І i. i 3: 5 і ке ио'шзгплен. ілкплсшшП при 411 °С 11(3-І 1
|
Рпс і_> Темперагурная іавіктіаосп» теплі емкс;тіі (кал/г^Н ) I in p іа и с-м - ipt in n ( I чше mi 70 О. ПОЧНЫЙ ПОТИС И рил: > - Пилі Ни пі.! i.> , . , , і.-н>"іі|нічііі<іП «(«'ни і up ' ('1111'' |
Введение пластификаторов вызывает снижение температуры стеклования с 61—62° до 30 °С (рис. 35).
Теплофизические характеристики полимерных материалов, исследовались многими авторами [158—167].
|
|
Рис. -53. Температурная завнснмостьРнс. 34. Температурная загшен-
Теплоемкостн мость теплоемкости ПОЛПВ1Н|ИЛ0
/—ЛИ1Ы-1И1ГО іі'.)лііміггіі. іиотикріілига; 2—лис - тнралеп.
LODoro......... .............. есхиги стекла [1641 /—ПВБ с 44-48% бутиральных групп и
|
|
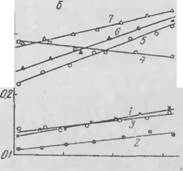
16% пластификатора, 2—то же беї пла стифнкатора; 3 — НВБ с 32—35 б>ти q ■ J01 q ральных групп
'20 40 60 ВО Г' С Рис. 33 Температурная зависимость. коэффициентов '/. (вт/и-граО). а (и*/сек), с [дж/къ-тград) некоторых промышленных полимерных маге
Риалов:
|
Я; |
/ — ЭД-5; - ип. ш. Ml, і: 1- ударопрочный пи нстпрол УПП-1 II ' 7 ислшфнрные 1-геп іонл. к-інкіі (ki
L. ih. М
В работах [1Г)8 160. 167] рассмагрнваютсн вопросы возможного прогнозирования і силовых свойств композиции па основе аморфного полистирола, при этом пспользуется модель Максвелла и соответственно формула смешения, выведенная тля теплопроводности смеси, в которой шарообразные частицы вкраплены во взаимосвязанную основу. Позднее эти результаты были использованы Энкеном для определения тснло-
|
R»»—-J |
|||||
|
100 |
200 |
3L |
То ту |
|
Рис. 36. Теплопроводность полистирола (втім ■ град) |
Проводностн смесей с частицами произвольной формы. Уравнение Максвелла в этом случае имеет вид
2V (К - К)
К —
2X0 4-^,, —v(X„ — К0) степень составляющей наполнителя.
V=
V» + v0'
Vn - объемная составляющая наполиптеля, Vo — объемная составляющая полимерной основы.
На рис. 37 и 38 приведены кривые температурной зависимости расчетных и экспериментальных коэффициентов теплопроводности композиций полистирола +6°/о н 2% (по объему) MgO. Частички MgO приближаются к дпаметрпческой форме с усредненным диаметром 0,001 мм.
Экспериментальные и расчетные значения коэффициентов теплопроводности композиции полистирол +2% MgO (табл 2?)) весьма близки по своим значениям и мало отличаются от іеплонроводпости чистого полистирола Ход экспериментальной п расчетом кривой тоже одинаков (рис. 37). Очевидно, в jtom случае частицы MgO не оказывают влияния па надмолекулярную і груктуру аморфного полистирола [167].
Їли композиции полистирол +6% MgO (табл. 29) наблю ые ся начительпое расхождение экспериментальных и расчетных значений.
|
ОП 0.І5 О;з |
|
2К |
|
■К |
|
(2.72) |
|
Где V |
•тн сравнить хот экспериментальной кривой па рис. 37 ття композиции полистирол +6% VigO заметен более ;'і1 і ■ .ем экспериментальной кривой
|
/—эксперимент: 2—расчет (2.72)
ВО ISO 2f0 3Z0 Г° К Pin - ЗЪ. Теплопроводность (ст/м ■ град) композиции полистирол 2% MgO: /—эксперимент; 2— расчет (2.72) |
|
А |
|
Характер подъема экспериментальной кривой па рис. 38 и большие по сравнению с расчетными экспериментальные значения указывают па изменение надмолекулярной структуры и увеличение сил межмолекулярного взаимодействия в аморфном полистироле. Температурные зависимости расчетных и экспериментальных значений. компоцизип полистирол +9.12 и 22с'0 талька представлены па рис. 39 и в табл. 30. Размер дііам&грнчеі" і частицы талька составляет 0,0015- 0.0100 им |
В работе [225] показано, что тепловое сопротивление основных валентных связей в аморфном полимере мало зависит от температуры. На рис. 37 пологий ход экспериментальной кривой аналогичен температурной зависимости Яэнсп чистого полистирола (рис. 36). В этом случае 2%-ное наполнение MgO еще не оказывает влияния на силы межмолекулярпого взаимодействия полимера.
А
|
Рис. 37. Теплопроводность (вт/м • град) ком позиции полистирола + 6% MgO: |
Тальк относится к слоистым силикатам. В отличие от MgO ■ альк имеет прямо пропорциональную температурную зависимость.
Значения?..,тп Для композиции с 6% MgO и с 9% талька отличаются незначительно, хотя теплопроводность талька ь диапазоне 80—370 К d среднем (в 15 -20 раз) ниже, чем у MgO.
Таблица 29
Расчетные и экспериментальные величины коэффициента теплопроводности композиции в функции от температуры |15К, 11>7|
|
X Мко |
|
Рлсч |
Полистирола
Полистирол - г С>"0 MgO
|
0,214 0/236 0,263 0,290 0,325 0,340 0,363 0 370 |
|
0,130 0,135 0,149 0,160 0,169 0,175 0,178 0,179 0,154 0,159 0,169 0,180 0,192 0,198 О 200 0,203 |
|
99,0 82,5 54,0 38.S 31,0 28,8 27,4 24,9 |
|
100 120 160 200 2-Ю 2й0 320 360 |
Полистирол + 2% MgO
|
99,0 82,5 54,0 38,5 31,0 28,8 27,4 24,9 |
|
0,130 0,135 0,149 0,160 0,168 0,175 0,178 0,179 |
|
0,138 0,143 0,153 0,170 0,180 0,186 0,189 0,190 |
|
0,167 0,176 0,186 0,193 0,200 0,206 0,208 0,211 |
|
100 120 160 200 240 280 320 360 |
Теплопроводность композиции полистирол +9% талька (рпс. 39) в исследуемом температурном диапазоне почти не изменяется. В зоне перехода от стеклообразного в высокоэла - огичпое состояние наолюдается аномальное изменение X с температурой (рис. 39). Очевидно, такая аномалия присуща roil части полимера, которая претерпевает изменения структуры в результате влияния твердой поверхности частиц наполнн - гелн По мере развития гибкости макромолекул и их пачечных образований с повышением температуры роль структурных изменений в полимере уменьшается и наполненная композиция ведет себя обычным образом — X проходит через макси мум п начинает уменьшаться.
Небольшой максимум кривой теплопроводности при температуре 273 СК (рис.39) обусловлен кристаллизационной водой, входящей в состав талька [159, 167].
Минеральный асбест был использован для наполнения в виде тонких гибких волокон длиной 2—10 мм и диаметром 0,02—0,01 мм.
Коэффициенты теплопроводности асбеста и талька в диа пазоне температур 80—370 °К имеют одинаковый ход темпера-
|
Рис. 39. Алис (ст/м ■ град) композитні полистирол + тальк: |
/ полис і и рол +9% талька; 2 — палпетнрол+ + 12% талька; 3—полистирол +22% талька
|
Таблица 30 Расчетные н экспериментальные величины коэффициента теплопроводности композиции в функции от температуры [158, I67J
|
Rpnoii зависимости и no своим значениям отличаются незначительно.
Экспериментальные значення /. композиции с 4 до 10% асбеста (рис. 40) ниже значении Х0ксп композиций с 9 и 12% талька (рис. 39).
В области стеклования на рис, 40 температурная зависимость теплопроводности имеет такое же аномальное изменение, как на рис. 39.
Кристаллизационная вода, входящая в состав асбеста, вы-
|
Рис. 40. Теплопроводность композиций полистирол + асбест: / шстирол + 111 асбест —полистирол +4 асб есті |
|
1С 41 Теплопроводі!! (от ц rn іпо. ІЦІНІ полп- стнрол+дрепесная мук; <>ЛІІІТІір< 1 - Чренеі-ЧІ І МКИ. І ар іич-поіі м кіт і п пні іт M-fKll |
Для компопіцпи с 10% асбеста теплопроводность no всем температурной диапазоне (рис. 40) так же как и цля композиции с ')% талька (рис 39), изменяется незначительно.
Температурные зависимости коэффициентов теплопровод - ностн композиций полистирол +20%-^ полистирол +40% и полистирол +60% древесной муки показаны па рис. 41.
Усредненная длина частицы древесной муки составляет і) " і і г Усредненная ширина частицы 0.1 0.12 чи.
Ввиду отсутствия данных по теплопроводности древесной муки в диапазоне температур 80—273°К приходится сравнивать экспериментальные значения к композиции с древесной мукой и к экспериментальные значения всех предыдущих композиции в диапазоне 273—380 °К-
Теплопроводность древесной массы (ель, сосна) в диапазоне 273—380 °К с учетом равновесного влагосодержанпя на ходится в пределах 0,3—0,4 вт/м-град.
С увеличением процентного содержания древесной мкп Яэксп композиций (рис. 41) увеличиваются также, как увеличивается теплопроводность двухфазной системы, модель которой положена в основу при выводе формулы Максвелла — Энке - на. На рис. 41 в ходе кривой теплопроводности при 7" = 273СК заметен небольшой минимум, что объясняется некоторой влажностью древесной муки. Отсутствие такого минимума на рис. 41 можно объяснить сравнительно небольшим наполнением композиции.
Наибольшее отклонение в изменении температурной зависимости п зоне стеклования наблюдается у композиции с 20% древесной муки. По мере увеличения содержания древесной муки объемная доля полистирольной основы уменьшается, что и приводит к постепенному сглаживанию максимума (рпс. 41).
В результате проведенных исследований стало очевидно, что введение в вязкотекучий аморфный полистирол частиц диаметрической формы с размером 1 —10 р при отсутствии химического взаимодействия оказывает существенное влияние на надмолекулярную структуру полимера даже при небольших концентрациях наполнителя.
Можно предположить, что в данном случае происходит взаимодействие молекул полимера с поверхностью частиц, при этом твердое тело оказывает влияние на прилегающие к нему слои жидкого полимера. Вероятно, такое явление не ограннчп вается прилегающим к поверхности мономолекулярным слоем, и особенности в свойствах обнаруживаются в слоях жидкого полимера толщиной в десятки и сотни молекул.
Подобное влияние, видимо, объясняется существованием расклинивающего давления, свойственного топким слоям жил кос ги, расположенным между любыми «ризами.
Расклинивающее давление — это не что иное, как и быт. н - пое по отношению к гидростатическому давлению окружающей жидкости давление, которое действует со стороны топкого слоя жидкости на ограничивающие его поверхности.
Расклинивающее давление вызывается частью силами отталкивания между наружными обкладками двойных ионных слоев, расположенных на поверхностях, ограничивающих пленку, частью силами молекулярного взаимодействия межд? молекулами пленки и прилегающими фазами.
С влиянием расклинивающего давления приходятся встречаться во многих явлениях оно препятствует слипанию BJBC шейных в жидкости частиц (в частности, коагуляции коллои - юв); мешает утончению и прорыву пленок между пузырьками пены. т. е. способствует устойчивости ее, может затруднить флотацию, противодействуя слипанию пузырьков воздуха с минеральными частицами.
Расклинивающее действие пленок между двумя твердыми телами способствует смазывающему н диспергирующему действию жидкостей.
В слоях жидкого полимера, прилегающих к поверхности твердоіі частицы вследствие ориентирующего действия поверхности, молекулы полимера могут располагаться в той пли иной мере упорядочеино. Особое строение этих слоев придает им характерные отличия в свойствах, которые выражаются в уве лнчепнп постоянной упругости сил Ваи дер Ваальса.
В конденсированных аморфных полимерах Ван дер Вааль - совы силы межмолскуляриого взаимодействия, как известно, ока іі. ів. нот решающее в. нотис па генлонерепос в аморфны полимерах.
Такие эффекты должны значительно усиливаться при высокой степени чнсперсности наполнителя. Данные для композиций с различной степенью дисперсности и формой частиц наполнителя достаточно хорошо согласуются с этим предположением.
Постоянные значения коэффициентов теплопроводности на рис. 8 указывают на возможность получения одинаковой теплопроводности композиции в достаточно широком температурном диапазоне, варьируя степень заполнения, теплопроводность, размер и форму частиц паполнптеля.
Аномальное отклонение кривой теплопроводности в зоік стеклования композиций с увеличенным и с нормальным вкладом теплопроводности основы можно объяснить пространственным поиядоченнем надмолекуляриоп структуры без изые нення постоянной упругости сил Ван дер Ваальса. При этом не исключена возможность небольшого изменения основных ва іентпьіх связен.
Композиции на основе кристаллического полиэтилена Полиэтилен высокой плотности низкого іавления. использованный в данной работе в качестве основы композиций, относится к частично крнсгаллп «шинным полимерам, теплопроводность которых падает с увеличением температуры
Композицию на полиэтиленовой основе можно представит;, как двухфазную систему, в которой чистины наполнителя дне нергнропаны в непрерывной полимерной среде. .Моделі, такой і ш темы положена в основу при ниво и - форм п, і Максвелла -)йкі и. т.
В композиции полиэтилен +19% А1203 окись алюминия диспергирована в виде шарообразных частиц размером 0,01 0,0015 мм. Теплопроводность А1203 изменяется обратно пропорционально температуре (табл. 31).
|
Г. "К |
|
® /го гдо гво ж "к І'іі,.-. -12 ТічиїоиропоАііогп. коміш. ніАіиі ноли jtdjimi+19% ЛІ2Оз [вт/м • гра<1). T чксіїі-римі-м'г; 2 расчет (2 72) |
|
ЦВ 0.7 (№ |
Расчетные величины к на рис. 42 и в табл. 31 находятся значительно ближе к экспериментальным, чем, например, композиции полистирол +6% MgO, хотя теплопроводности AljOj II MgO почти одинаковы (табл. 29, 31). Объясняется это
|
Полиэтилен - j - 19% А1203 |
||||
|
100 |
120,0 |
0,400 |
0,780 |
0,920 |
|
120 |
97,0 |
0,463 |
0,772 |
0,915 |
|
160 |
60,0 |
0,440 |
0,742 |
0,911 |
|
200 |
44,0 |
0,426 |
0,721 |
0,892 |
|
240 |
37,5 |
0,411 |
0,688 |
0,867 |
|
280 |
34,5 |
0,393 |
0,673 |
0,822 |
|
320 |
31,5 |
0,363 |
0,625 |
0,750 |
|
360 |
30,5 |
0,322 |
0,551 |
0,668 |
|
Таблица 31 Расчетные и экспериментальные величины коэффициента теплопроводности композиции в функции от температуры [189, 160, 167] |
|
Льо, |
|
Полиэтилена |
Тем, что композиции на основе полиэтилена лучше соответствуют примененной для расчетов двухфазной модели, чем композиции на полистирольной основе. Некоторое увеличение экспериментальных данных на рис. 42 может быть обусловлено структурной перестройкой аморфной фазы, объемная доля которой составляет 15%.
А
При введении в полиэтилен А120з частицы наполнителя являются зародышами кристаллического структурообразования. Влияние этих частиц сводится к тому, что оии, оставаясь неизменным п в расплаве полимера, при охлаждении расплава являются центрами, вокруг которых начинается кристаллизация полимеров с образованием сферолитпон или другой надмолекулярной структуры.
Так как число таких центров можно задавать количеством введенных частиц, то появляется возможность регулирования процесса кристаллизации и структурообразования. Наличие искусственно введенных зародышей создает условия для получения однородно закристаллизованных полимеров с надмолекулярной структурой, обеспечивающей нужный комплекс свойств. Надмолекулярные структуры, полученные па искусственно введенных зародышах, более устойчивы к тепловым и другим воздействиям.
Исследования, проведенные в работе [218], показали, что форма частіш зародышеобразователей оказывает существенное влияние на надмолекулярную структуру кристаллического полимера. При введении искусственных зародышей, частицы которых имеют анизодиаметрическую форму, в полимере образуются характерные определенно ориентированные кристаллические структуры в виде лепт. Если учесть, что кристаллы полимера имеют анизотропное строение, то появляется возможность, используя топкие ориентированные волокна диаметром порядка 0,001 мм, получить кристаллический полимер с анизотропной теплопроводностью. У такого полимера кристаллы должны быть ориентированы вдоль волокон наполнителя.
Варьируя количество введенных зародышей, их размеры и форму, можно получать полимерные образцы с различной надмолекулярной структурой, устойчивой к тепловым, воздействиям.