Температурно-временная зависимость длительной прочности полимербетонов
Применение полимербетонов в качестве несущих конструкций промышленных зданий и сооружений в условиях воздействия различных агрессивных сред не только рациональное и экономически оправданное, но в некоторых случаях и единственно возможное решение. В то же время широкое внедрение в практику строительства полимербетонов сдерживается рядом причин, главными из которых являются отсутствие надежной и практически
удобной оденки длительной прочности и деформационных характеристик полимербетонов и методов расчета несущих конструкций на их основе.
Специфические свойства полимерных материалов определяют всю сложность разработки единой теории и методов расчета длительной прочности и деформатив - ности конструкционных элементов на их основе [28, 48, 71, 100, 145].
Известно, что реальная прочность большинства технических материалов на несколько порядков ниже теоретической, рассчитанной исходя из сил межмолекулярного взаимодействия. Объяснение этого расхождения впервые было дано А. Гриффитом. Он предположил наличие, в твердом теле зародышевых трещин и показал, что напряжения в их вершинах совпадают с теоретической прочностью материала, а средние напряжения, приложенные к материалу в момент разрушения, являются мерой его технической прочности.
На основании этих представлений была предложена статистическая теория хрупкой прочности. Однако в соответствии с этой теорией трудно объяснить зависимость прочности от продолжительности действия нагрузки и составить представление о критическом характере разрушения. В более поздних работах показано, что полимерные материалы разрушаются в результате процесса, развивающегося непрерывно во времени, а время до полного разрушения в значительной степени зависит от продолжительности действия нагрузки и температуры среды.
Для определения длительной прочности полимерных материалов, имеющих хрупкий разрыв, С. Н. Журков предложил уравнение:
T = T0ec/»-Y6/<^)) (62)
Из которого вытекает, что при постоянной температуре
Б = б0 — const lg Т/То, (63)
Где х—время до разрушения материалов при напряжении а; t/0 и то — константы, характеризующие материалы; у — структурный коэффициент; Т — абсолютная температура; К — универсальная газовая постоянная; о0 — абсолютный предел прочности полимерного материала, о'о = С/0у.
Уравнение (63) показывает, что прочность существенно зависит от времени действия приложенной нагрузки: чем больше это время, тем меньше конечная прочность.
Из формулы (62) следует, что с повышением температуры прочность полимеров также падает. При заданном времени действия приложенной силы влияние температуры до определенного предела носит линейный характер:
Б = б0 - const Т. (64)
Хотя зависимость (62) и позволила избежать противоречий, характерных для статистической теории прочности, однако она не лишена и некоторых недостатков. Если о-»-0, длительная прочность образца ограничена, а если o=o0 = U0/T, длительная прочность оказывается независимой от температуры, что нарушает физический смысл формулы (62). В [29, 46] дана теоретическая зависимость, освобождающая формулу (62) от физических парадоксов.
Многочисленные экспериментальные исследования показали, что величина то лежит в пределах от 10~12 до 10~13 (табл. 70). Это значение очень близко к периоду колебаний атомов в твердом теле. Поэтому при прогнозировании длительной прочности константу То, как правило, можно не определять. Отсюда вытекает весьма важный вывод о том, что длительная прочность при прочих равных условиях характеризуется лишь двумя коэффициентами U0 и V, которые можно назвать константами материала. Следовательно, для прогнозирования долговечности полимербетонов необходимо экспериментально определить эти коэффициенты.
|
Таблица 70. Константы полимерных материалов и полимербетонов на основе КФ-Ж и ПН-1
|
Приведенные выше формулы, характеризующие длительную прочность, справедливы только в том случае, если у исследуемых материалов закончились все физико - химические превращения и они обладают стабильными свойствами.
В процессе отверждения крупногабаритных полимер бетонных изделий и конструкций в материале возникают значительные температурные и временные усадочные внутренние напряжения, приводящие в некоторых слу чаях к нарушению его монолитности. Положение усугуб ляется тем, что такие конструкции предназначены дл5 использования в условиях воздействия различных агрессивных сред, которые, в свою очередь, нарушают ста бильность структурного состояния материала. Поэтому необходимо подробнее рассмотреть физическую сущності математического выражения температурно-временной зависимости прочности таких материалов.
Известно, что в стабильных температурно-влажност - ных условиях для каждого вида материала и характера напряженного состояния все члены, входящие в формулу (62), кроме структурного коэффициента у, имеют однозначное конкретное значение. Структурный коэффициент у = |Зсо (со— флуктуационный объем элементарного акта разрушения, —-коэффициент концентрации напряжений) характеризует структурное состояние материала и равномерность распределения напряжений внешнего силового поля. Коэффициент 3, в свою очередь, зависит не только от температуры, но и от приложенного напряжения, так как эти параметры определяют скорость релаксационных процессов. Таким образом, даже в стабильных условиях коэффициент 3 изменяет свое значение.
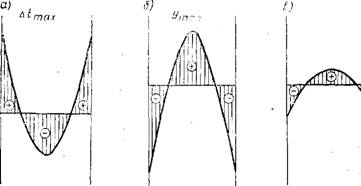
Например, начальное отверждение натурных конструкций из полимербетонов во многих случаях происходит при обычной температуре окружающей среды, т. е. в изотермических условиях с выделением значительного количества теплоты в окружающую среду. В этом случае в начальный момент по всему сечению изделия имеется равномерное температурное поле Оо (рис. 49,а). С началом процесса отверждения вследствие экзотермического саморазогрева, теплообмена с окружающей средой и относительно низкой теплопроводности полимербетонов температурное поле становится неравномерным по сечению с максимумом в центре сечения (рис. 49,6). По мере развития процессов полимеризации (или поликонденсации) этот эффект усиливается и разность температур At между наружными поверхностями изделия и его центром быстро возрастает (рис. 49,в).
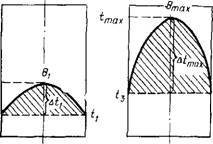
С повышением температуры изделие должно расширяться в результате температурных деформаций. Образование в процессе полимеризации химических связей сопровождается развитием усадочных деформаций. Естественно предположить, что к моменту достижения максимальных температур эпюры внутренних напряжений будут выглядеть так, как это показано на (рис. 50), и температурные напряжения будут компенсироваться усадочными напряжениями. Однако опыт показывает, что в ряде случаев разрушение происходит под действием температурных напряжений.
В работе [105] установлено, что усадочные деформации запаздывают и отстают по времени от температурных деформаций. Отсюда вытекают весьма важные следствия: 1) усадочные деформации развиваются несколько позже температурных; 2) при высоких температурах экзотермического саморазогрева температурные деформации и соответствующие им внутренние напряжения могут приводить к нарушению монолитности изделий; 3) несовпадение по времени температурных и усадочных внутренних напряжений позволяет определять их раздельно.
Таким образом, нельзя допустить, чтобы в реальных конструкциях в процессе формования и отверждения возникали высокие температуры и соответствующие им температурные напряжения. До начала организации выпуска каждого изделия или конструкции необходимо предварительно определять максимально возможные температурные напряжения. Формулы для определения температурных напряжений известны. Однако при выводе указанных формул предполагалось, что модуль упругости и коэффициент температурных деформаций материала остаются постоянными.
Нелинейное распределение температуры по сечению изделия, переменные модуль упругости и коэффициент температурных деформаций, наличие релаксационных процессов настолько усложняют предложенную методику расчета, чго ее практически невозможно использовать для расчета температурных напряжений полимербетонных конструкций.
Нами показано, что модуль упругости полимербетонов существенно зависит от температуры и может быть описан экспоненциальной зависимостью:
|
193 |
7 Зак. 25(1
|
Рис. 50. Эпюры внутренних напряжений по сечению изделия А — под действием температурных деформаций; б— то же, усадочных; в — суммарная эпюра внутренних напряжений |
Где Еі — модуль упругости полимербетона при нормальной температуре; «■—коэффициент, для полиэфирных и фурановых смол а = 0,055; t — температура полимербетона.
Исследования свидетельствовали, что в пределах от нуля до 100°С кратковременная прочность и модуль упругости полимербетонных призм уменьшаются пропорционально повышению температуры. Следовательно, в процессе отверждения полимербетонов предельное значение модуля упругости характеризуется температурой саморазогрева и не может быть выше соответствующего модуля упругости для отвержденных образцов.
|
A) S) В) |
|
Рис. 49. Распределение температуры саморазогрева по сечеиию изделия |
Коэффициент температурных деформаций полимербетона при изменении температуры от 20 до 100°С также изменяется линейно в пределах 19- 10~4—13- 10~4.
На основании статистической обработки результатов испытаний нами предложена сравнительно простая формула, позволяющая с достаточной для практических целей точностью определять максимальные температурные напряжения:
Б, =(£„—/( Uак) 1 О3 (а /мак _ а ) М1 — и), (66)
Где at—максимальные температурные напряжения; Ео — модуль упругости при 0°С; К — коэффициент пропорциональности, К = = 0,9 Па-°С; ti н /МаК — температура саморазогрева соответственно на поверхности и в центре сечения; а—коэффициент температурных деформаций; (х — коэффициент Пуассона, = 0,22...0,275; г|) — коэффициент релаксации температурных напряжений, 0,6...0,7.
Таким образом, изменения структурного состояния полимербетонов могут быть учтены только в том случае, если коэффициент (3 будет отражать алгебраическую сумму всех напряжений, возникающих в материале:
Р = р, + б, + бу + би, (67)
Где Р — суммарный коэффициент концентрации напряжений; [3; — напряжения от внешних силовых нагрузок; о'(; о'у; о'ь — напряжении соответственно температурные, усадочные н влажностные.
Следовательно, в структурный коэффициент у должен входить суммарный коэффициент р.
Меньшей однородностью и значительными собственными напряжениями можно, по всей вероятности, объяснить то, что коэффициент у для полимербетонов более чем на пооядок выше аналогичных величин для ненапол - ненных термопластичных материалов (см. табл. 70).
Уравнение (62) можно записать в виде:
Б = (7о /у — (К Т/у) 1п (т/то). (68)
При условии Т== Тг = const из выражения (68) следует, что действующие в материале напряжения линейно связаны с логарифмом долговечности материала. Таким образом, для прогнозирования долговечности материала в условиях совместного воздействия нагрузки и температуры необходимо определять величины г/о И V.
|
195 |
С точки зрения кинетической концепции прочности, процесс разрушения при совместном воздействии нагрузки и агрессивной среды надо рассматривать как процесс, развивающийся в материале во времени. Поэтому характеристикой разрушения может быть скорость накопления микроразрушений от нагрузки Vn и от действия агрессивной СреДЫ Ка. Результирующая скорость разру-
7* Зак. 251
|
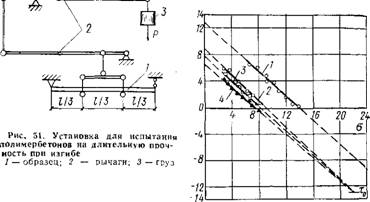
Рис. 52. Изменение долговечности в зависимости от напряжений и температуры /—легкий полимербетон ПН-1 при 20°С; 2, 3 и 4 — легкий по-шмербетон КФ-Ж при 20, 60 и 80?С соответственно ШЄНИЯ У сум в каждый момент времени т в первом приближении можно определить по формуле: |
УсУм(т) = Ун(т) + Уа(т), (69)
Где Vu(x)—скорость разрушения материала от действия нагрузки; Va (т)—скорость разрушения материала от действия агрессивной среды.
Предположение, что результирующая скорость разрушения определяется суммой скоростей от каждого воздействия в отдельности, является наиболее простым, однако оно не подтверждается экспериментальными данными.
Для соответствующих долговечностей имеем 1/ТсУм = 1/Тн + 1/Та ИЛИ Тсум = Та Т„ /(та + Тн ). (70)
Экспериментальное определение долговечности полимербетонов под действием нагрузки и температуры окружающей среды при растяжении при изгибе проводилось на специальных установках (рис. 51). Варьируя нагрузку и температуру с помощью специального приспособления, прослеживали изменение долговечности в широких пределах от секунд до нескольких месяцев.
Полученные экспериментальные данные в координатах lgr — о приведены на рис. 52. Их математическая обработка показала наличие линейной связи как при растяжении, так и при изгибе. Уравнения связи для рассматриваемых полимербетонов приведены в табл. 71.
Экстраполяция зависимостей lgr — о для полимербе-
|
Таблица 71. Основные константы исследованных полимербетонов
|
Тона КФ-Ж показывает, что все три прямые пересекаются в одной точке с ординатой lg т = 13 или то=Ю-13с, что не противоречит имеющимся данным (рис. 52).
Зная То--=10~13 с, можно определить U0 и у, входящие в уравнение (62). Из уравнения (62) следует:
U0 = V в = 2,303 /С 7- (lglgт0). (71)
Величины, входящие в первую часть уравнения (71), известны, следовательно, для различных значений — уст можно вычислить ст. Результаты расчета по формуле (71) для состава на КФ-Ж приведены на рис. 53. Найденные величины при различных температурах достаточно хорошо легли на прямую, отвечающую уравнению U = = U0 — ус, из которого можно определить U0 и 7 (см. табл. 71).
Получив значения то", U0 и 7, можно определить долговечность Тп, пользуясь формулой (70).
В условиях действия агрессивных сред большинство полимерных материалов, в том числе и полимербетоны, с течением времени снижают свою прочность. Изменение прочности полимербетона при растяжении, изгибе в зависимости от времени пребывания в агрессивной среде Та может быть представлено в виде
6а /бо = ~т'т£ , (72)
Где Сто — условная прочность при скорости нагружения 0,1—0,2 МПа в 1 с; та — время пребывания в агрессивной среде, с; п и т — постоянные, зависящие от вида материала и вида агрессивной среды; Ста — прочность материала после пребывания в агрессивной среде в течение времени т, МПа.
|
'"І |
|
Ltffek |
При этом зависимость (72) применима при Та^ЗО сут.
С/, кВж/моль тм
|
Ч Ч X Ч |
||||
Bk_________ ._________________________________________________
В 6,МПа
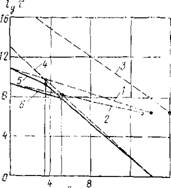
Рис. 53. Зависимость энергии активации от напряжения для полимербетонов КФ-Ж 9 □ и Д — результаты получены при 20°С; 2, 3 и 4 — легкий полимербетон КФЖ при 20°, 60° и 80°с соответственно
Рис. 54. Изменение долговечности полимербетона ПН-1
1 — в H2S04 10%-ной концентрации:
|
12 16 б, МПа |
|
Бгр бгр |
2 — в воде; 3 — в H2SOi 30%-ной кон цеитрации; 4 — при действии механической растягивающей нагрузки; 5 — при совместном действии механической нагрузки и H2SOi 10%-ной. концентрации; 6 — при совместном действии механической нагрузки и воды
На основе формулы (72) долговечность полимербетона в условиях воздействия агрессивных сред и при отсутствии внешних нагрузок можно выразить в виде
Та = Km бо) ■ (73)
Это выражение позволяет, задавшись допустимым снижением прочности материала, вычислить его долговечность в этих условиях.
|
12В |
|
117,6 |
|
109,2 |
|
100,8 |
|
92А |
Для полимербетонов К. Ф-Ж И ПН-1 были определены
постоянные in и п при воздействии воды и растворов H:'S04 10%- и 30%-ной концентрации (табл. 72).
|
Таблица 72, Изменение коэффициентов а и щ в зависимости от вида агрессивной среды
|
Анализируя полученные зависимости суммарной долговечности (рис. 54) ОТ Тн И Та следует отметить, что графики суммарной долговечности имеют переломы при некоторых уровнях напряжений а1р. В области о> >Grр определяющее влияние на долговечность оказывают механические нагрузк и, так как тн<Ста, а в области о<.аГр определяющее влияние на общую долговечность оказывает агрессивная среда, так как тн^>та.
Предложенная методика была использована при расчете долговечности полимербетонных колонн подванных эстакад цехов электролиза меди, эксплуатируемых в условиях совместного действия нагрузок, повышенных температур и проливов растворов серной кислоты. Многолетний опыт эксплуатации несущих полимербетонных конструкций доказал' правомочность использования данной методики для прогнозирования аналогичных конструкций из различных видов полимербетонов.
Экспериментально-теоретические исследования по определению методики расчета и прогноза долговечности химически стойких полимербетонных конструкций, выполненные в лаборатории полимербетонов НИИЖБа, подтверждаются успешной многолетней эксплуатацией многих конструкций и сооружений из полимербетонов. Так, на Балхашском горно-металлургическом комбинате одна из ванн Электролиза меди из полимербетона на связующем ФАМ эксплуатируется около 20 лет и до настоящего времени находится в хорошем состоянии. Так же, как и полимербетонные тротуарные плиты размером 500X500X30 мм на основе полиэфирной смолы Г1И-1, уложенные на опытном участке ПИИЖБа в 1967 г.
Изготовленные в 1968—1970 гг. 16 полимербетонных травильных ванн размером 2000X1200 мм. Их практически не ремонтировали в течение 10—12 лет (Днепропетровский трубопрокатный завод).
Корецкий В. 1І. [77], проводя тщательные натурные обследования полимербетонных облицовок водоскатов семи эксплуатируемых гидротехнических сооружений Средней Азии (четыре из них построены в 1962—1964 гг.) установил, что для водозаборных сооружений на предгорных участках рек характерны короткие паводковые периоды, когда через гидросооружения сбрасывается 60—80% годового стока и донных наносов. В межпаводковые периоды сооружения, как правило, свободны от воды, в это время разрушительное действие наносов и воды сменяется атмосферным воздействием и высокой солнечной радиацией.
На основании результатов натурных обследований и испытания кернов, взятых из полимербетонных облицовок после 12—13 лет эксплуатации, были получены убедительные данные о высокой надежности и долговечности полимербетона, воспринимающего весьма жесткие внешние воздействия. Hanpiwvp, на Сары-Курганском, Беш - Алышском, Караснансічом и других гироузлах за год проходит 40—100 тыс. м3 наносов со средней крупностью 40—50 мм. При гаком интенсивном воздействии наносов полимербетонные облицовки изнашиваются в значительно меньшей степени по сравнени'о с облицовками из железобетона и каменного лить» [77].
Расчеты по предложенной в НИИЖБе методике показывают, что прогнозируемая долговечность полимербетонных конструкций в зависимо :і и от вида полимербетона и условий эксплуатации може г составлять от 20 до 40 лет. По данным Корецкого В. I!.. прогнозируемая долговечность облицовок на основе колиviepoeгона ФАМ равна 30—40 лет, т. е. результаты в обої х. случаях нрак - іически совпадают. Расчет производился в соответствии с методикой, приведенной в ГОСТ 258М—83.
Исследования А. И. Чебаненко |145| позволили уста новить четко выраженные релаксационные и гистерезис - ные свойства полимербетонов, обусловленные активним проявлением энтропийной упругости полимерной матрицы. На основании этих исследований А. И. Чебаненко разработал основы теории расчета армополимербетон - ных конструкций, основные положения которой заключаются в следующем:
В методике расчета учитывается комплексная оценка механических и деформационных свойств полимербетонов, которая осуществляется с помощью структурных диаграмм. Контуры этих диаграмм устанавливаются по четырем признакам: кратковременной и длительной прочности, начальному модулю упругости и предельной равновесной деформации;
Учитывается влияние физической нелинейности механических характеристик полимербетонов, которые предварительно получили строгую математическую интерпретацию;
Оцениваются реологические свойства материала исходя из параметрической теории ползучести;
Учитываются особенности предварительно напряженных армополимербетонных конструкций с металлической и неметаллической напрягаемой арматурой. При этом расчетные формулы базируются на общепризнанной методике по I и II группам предельных состояний, гарантирующих иадел-шость эксплуатационных характеристик[13].
Базируясь на теории расчета армополимербетонных конструкций В. Е. Беляевым [34] предложена теория расчета армополимербетонных конструкций, которая учитывает одновременное воздействие внешних нагрузок и температуры. Основные положения этой теории отражены в «Руководстве по проектированию полимербетонных конструкций на полиэфирных смолах».