Основные уравнения гидродинамики и теплообмена водопарового тракта
Гидродинамические и теплообменные процессы водопарового тракта парового котла и парогенератора протекают в трубах. Стенки труб обладают определенными свойствами: теплопроводностью, теплоемкостью, массой. На поверхности труб протекают соответствующие процессы с окружающей средой на наружной стенке и рабочей средой — на внутренней стенке. Свойства стенок труб и протекающие на этих стенках процессы учитываются граничными условиями уравнений, описывающих процессы, которые имеют место в водопаровом тракте. Такими уравнениями являются: уравнения материального баланса, баланса энергии потока рабочей среды и ограждающей стенки и уравнение движения (или количества движения).
Все эти уравнения рассматриваются в курсах гидромеханики и теплопередачи и потому их выводы здесь не излагаются.
Запишем уравнения в окончательном виде: материального баланса
(9.1)
Баланса энергии потока рабочей среды ИЁй їІШ — л ■
Dz "+"' д* ~~ Vbh'
Теплового баланса для обогреваемых стенок канала
= (9.3)
В формулах (9.1) —(9.3) G, р, г —расход рабочей среды через канал, ее плотность и энтальпия; f — сечение канала; г — координата, совпадающая с направлением движения рабочей среды; qBB, ?нар — линейная плотность потока тепла на внутренней и наружной поверхностях канала; т — линейная масса металла стенок канала (масса стенок трубы длиной 1 м); tM, см — температура и теплоемкость металла; а — коэффициент теплоотдачи от стенки к рабочей среде; Я — внутренний периметр сечения канала (для трубы П= =1ТС? вб) •
Специфической формой записи второго закона механики применительно к течению среды в канале является
Dp dw, dw і, w'p і. /п л - ЗГ = P 7ЙГ + fz + k IT ± s:m (9-4)
Его называют уравнением движения или уравнением сохранения количества движения. Интегрирование (9.4) в пределах от начала канала z=0 (w=wu р=рі) до конца в общем случае до сечения z—l (w—wi, р=р%) дает интегральную форму уравнения движения
TOC o "1-3" h z I Ws
Pi ^ dzAr ^ {w?)dw--
6 Wi
I h
+ Щ dz± g?dh (9.5)
О b
Где h=t sin a.
Из (9.5) следует, что перепад давлений в канале Ap=pi—р2 затрачивается на преодоление следующих сил, возникающих при движении в нем среды:
Сил трения (коэффициент пропорциональности k определяется экспериментально, его значение связано с коэффициентом трения соотношением k=%/d)
О
Сил, обусловленных неоднородностью скоростей на входе и на выходе канала — ускорением потока, .т. е. неоднородностью поля скоростей по длине канала,
W,
^ (дар) dw,
А>,
Сил, обусловленных неодинаковостью ПОЛЯ скоростей во времени — инерционной составляющей перепада давления, неравной нулю только в нестационарных процессах, і
Г dw j
Составляющей силы тяжести — нивелирной составляющей, определяемой средней плотностью и разностью высот, т. е. разностью уровней (эта величина выражает гидростатическое давление столба среды высотой h), h
G?dh.
О
Итак, гидродинамические и теплообменные процессы, протекающие в водопаровом тракте, описываются системой уравнений: баланса массы (9.1), баланса энергии для потока рабочей среды (9.2), теплового баланса для обогреваемых стенок канала (9.3), движения (9.4). Эта система уравнений дополняется еще уравнением состояния
Р=р (р, і), (9.6)
Выражающим зависимость одного термодинамического параметра от двух других, а также эмпирическими зависимостями для коэффициента теплоотдачи а, коэффициента трения k. Система уравнений (9.1) — (9.4) и (9.6) совместно с эмпирическими зависимостями для а и % является замкнутой: в ней число неизвестных (G, р, i, tit, р) равно числу уравнений (так как w=G/fp). Внешние воздействия для этой системы: qnар, GBX, івх, GBax заданы.
В стационарном режиме все производные по х в уравнениях (9.1) —(9.4) и (9.6) равны нулю, а все параметры являются только функциями координаты г и потому фундаментальные уравнения приобретают следующий вид: уравнение сохранения массы
Уравнение (9.3) системы (9.1) — (9.4) и (9.6) исчезает, так как <7Вц=<7нар=<7. Из (9.7) следует, что в стационарном режиме массовый расход в любом сечении канала одинаков G (z) —const. Из (9.8) с учетом последнего результата следует:
_dl__ J7_
Dz G
Или
9.2. характеристики движения пароводяной смеси
Основные характеристики течения пароводяного потока:
Массовая скорость среды wр (воды, пара, пароводяной смеси). Охлаждающее действие потока зависит не только от его скорости w, но и от плотности р. Охлаждающий эффект потока принято оценивать по произведению этих параметров, т. е. через массовую скорость wp, кг/(м2-с), представляющую собой массовый расход, отнесенный к единице сечения трубы:
|
Wp- |
|
F |
G
Скорость циркуляции Wo, м/с — скорость воды при температуре насыщения, соответствующая расходу рабочего тела в трубах:
Где Gсм — массовый расход пароводяной смеси через систему труб, кг/с (при поступлении воды в парообразующие трубы GCm=Gb); f — сечение для прохода рабочей среды, м2; р'— плотность воды при температуре насыщения, кг/м3.
Приведенная скорость воды
W'o, м/с —
|
(9.11) (9.12) |
Скорость, которую имела бы вода, проходящая через данное сечение парообразующей трубы, при условии, что она занимала бы все ее сечение:
|
W, |
|
H' |
G„
(9.15)
Нии wa<iwB; разность их равна относительной скорости пара
Wr=Wu—WB. (9.17)
Относительная скорость пара оказывает существенное влияние на закономерности движения пароводяной смеси (см. § 12.1).
Массовое паросодержание х — массовая доля расхода пара в потоке пароводяной смеси при Wo—Wb'
X—Gn/GcM - (9.18)
Для равновесного термодинамического течения массовое паросодержание выражают также формулой
X==^tzJLt (9.19)
Где іпот — удельная энтальпия потока в рассматриваемом сечении системы труб, кДж/кг; І' — удельная энтальпия воды на линии насыщения при давлении в данном сечении, кДж/кг; г — теплота фазового перехода при том же давлении, кДж/кг.
Массовое водосодержание
1-JC<=1-(9.20)
"см исм
|
См __ °П+ б fp' |
|
G, |
|
W,: |
Скорость пароводяной смеси Wcm, м/с. Используя выражение для скорости циркуляции, запишем:
-JL(9.21)
Fp'
В свою очередь массовые расходы, кг/с, воды и пара соответственно равны:
G.=VBP/=m»/OP7;
G„= Vпр"=w" о(>" f,
Где VB и Vn — объемные расходы воды и пара, м3/с.
После подстановки GB и Ga в (9.21) получим:
Приведенная скорость пара w"0, м/с — скорость, которую имел бы пар, проходящий через данное сечение парообразующей трубы, при условии, что он занимал бы все ее сечение
|
W |
|
F Р" |
Gn
Где Gn — массовый расход пара через систему труб, кг/с; р" — плотность пара, кг/м3.
Относительная скорость пара wr, м/с. Истинные скорости воды и пара отличаются от расходных, так как в реальных условиях в совместном движении вода и пар, составляющие пароводяную смесь, движутся не с одинаковой скоростью, WuҐ=W-B-
|
--W' |
|
- W |
|
Av |
В восходящем потоке пар движется быстрее воды, т. е. т>п>дав; при опускном движе(9.22)
О р'
Скорость пароводяной смеси записывается как отношение суммы объемных расходов составляющих ее компонентов Fn+Fs к суммар ному сечению для прохода потока
F
Или с учетом GB и Gn
W' о из уравнения
Подстановка в (9.24) дает:
Часто бывает необходимо выразить wcм через массовое паросодержание х. Принимая во внимание, что сумма сечений, занятых паром /п и водой /в, равна f, имеем зависимость
(9.26)
FnWu+f в®в — Wcm f,
Которая переписывается так:
|
-х) V'. |
|
(9.27) (9.28) из (9.27), |
Gnt/' + GBf '=GcmVCM,
Откуда
On
Или
Vcm—XV"-- (1 -
Известно также, что
""см ^
Подставляя в (9.28) значение получаем:
|
Wr |
|
V |
IGpm:i' Г, і / v"
Л-- f 1 I Л
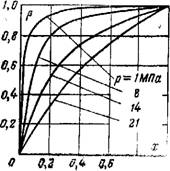
На рис. 9.1 показана связь между массовым х и объемным р паросодержанием потока. При низких давлениях очень велико влияние х в области его малых значений. С ростом давления это влияние уменьшается. При любом давлении d$/dx уменьшается с ростом х. Эти закономерности оказывают существенное влияние на режимы течения двухфазного потока в трубах и их температурный режим.
Напорное (истинное) паросодержание q>— доля сечения трубы, занятая паром, fn, соответствующая истинной скорости воды и пара:
<P=/n/f. (9.32)
|
Vn |
|
(9.33) |
|
3 - |
|
Уп + Va |
Напорное паросодержание ф отвечает наличию относительной скорости пара wr, т. е. ffi'n^ttv Как отмечалось ранее, расходное паросодержание предполагает равенство скоростей пара и воды Связь между этими параметрами течения
J^nfn u>cj
Откуда
|
41- г |
(9.34)
|
(9.31) |
Или
W,
Объемное расходное паросодержание p. Объемная доля пара в потоке пароводяной смеси при одинаковой скорости воды и пара называется объемным (расходным) паросо - держанием
(9.30)
^ V7.. + Va а с учетом (9.18) и (9.20)
1 +
|
О, В ко Рис. 9.1. Зависимость объемного паросодержания р от массового паросодержания х при различных давлениях. |
Обозначая /w п—с, получаем!
Ф=ср. (9.35)
При подъемном движении
Wn>WcM с<1; ф<р. В опускном движении
Шп<а>см; с> 1; ф>р.
Если принять Wn=WB = WcM, то с=1,
Ф=р. (9.36)
Коэффициент пропорциональности с характеризует отношение скоростей пароводяной смеси t0см и действительной скорости пара wn и потому учитывает относительную скорость пара wr. С повышением давления относительная скорость пара падает и по мере приближения к критическому давлению с-*~1, а ф->-р.
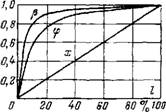
По длине равномерно обогреваемой парообразующей трубы массовое паросодержание изменяется линейно, приобретая крайние значения; на входе х—0 (если іВх=і'), на выходе X—1 (если івмх=і") (рис. 9.2). В то же время объемное паросодержание р и истинное ф, имея на входе также нулевые значения, резко возрастают на начальном участке канала. Далее интенсивность роста р и ф убывает, приобретая в конце парообразующей трубы максимальное значение. равное единице. С повышением давления ф и р приближаются к значению х.
|
|
|
Рис. 9.2. Изменение Р, ф и х по длине парообразующего канала. |
Напорное паросодержание ф является важной характеристикой потока, поскольку оно отражает реальное распределение воды и пара и их индивидуальные скорости в совместном движении пароводяной смеси.
Действительная скорость пара
Иуп=ш"0/ф - (9.37)
Действительная скорость воды
Ш>в=ш'о/( 1—ф). (9.38)
Расходная плотность пароводяной смеси Рем, кг/м3 — плотность, соответствующая одинаковой скорости воды и пара:
Рс (9-39)
Действительная (истинная) плотность пароводяной смеси рн, кг/м3, соответствующая истинным значениям скорости пара и воды, определяется на основании следующих рассуждений. Выделим элемент трубы высотой Aft, заполненный пароводяной смесью (рис. 9.3). Представим далее весь пар и всю воду в виде соответствующих элементарных объемов. Части сечений, занятые паром и водой, обозначим /п и /в, а сумму их f. Соответствующие значения массы обоих компонентов выражаются через /пЛ/ф" и /вА/гр£, сумма которых равна массе выделенного объема пароводяной смеси fA/грн- Отсюда получаем выражение для действительной плотности смеси
Рн = р'_ф(р'_р") = (1-ф)р'+фр". (9.40)
Относительная скорость пара при восходящем движении приводит к уменьшению доли сечения, занятой паром ф, и соответствующему увеличению доли сечения, занятой ВОДОЙ (1—ф), в СВЯЗИ с чем Рн>Рсм - С ростом давления
—^Рсм-
Кратность циркуляции К — величина, обратная массовому паро - содержанию, выражает отношение количества
Циркулирующей воды к количеству получаемого пара за один и тот же промежуток времени (см. § 1.2)
К=1/х. (9.41)