Основные публикации по солнечной энергии
Отношение потоков прямой солнечной радиации на наклонной и горизонтальной поверхностях
|
|
При проектировании солнечных установок часто возникает необходимость пересчета данных по часовому приходу радиации на горизонтальную поверхность (измеренную или рассчитанную методами,
|
|
|
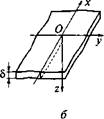
Фиг. 3.6.1. Приход радиации на горизонтальную и наклонную поверхности. |
|
|
|
|
|
|
|
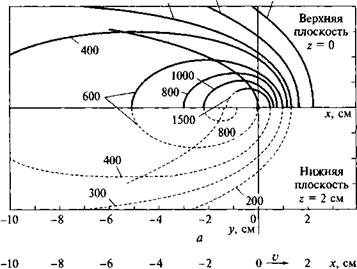
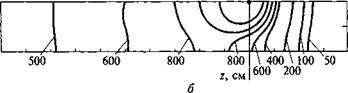
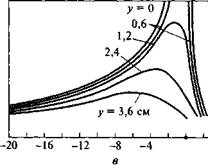
Фиг. 3.6.2. Кс'синус угла падения прямой радиации на поверхности, наклоненные к экватору, для различных значений <р — « [7]. |
описанными в разд. 3.5) на данные по приходу радиации на наклонную поверхность. С достаточной степенью точности это можно сделать для прямой и рассеянной составляющих радиации участка небосвода, включающего Солнце. Методы подобного пересчета для рассеянной составляющей будут рассмотрены в разд. 3.7.
Для определения угла падения прямой радиации как на горизонтальную, так и на наклонную плоскость (если поверхность наклонена на север или на юг, т. е. если у = 0°) могут быть использованы уравнения (2.5.3) и (2.5.4). Из фиг. 3.6.1 следует[6], что Н = Ипсos ©z и Нт = Нпcos ©т. Отношение потока радиации Нт, падающего по нормали на наклонную поверхность, к соответствующему потоку радиации И, падающему на горизонтальную поверхность, может быть выражено через углы ©г, ©т и поток радиации Нп, падающий в рассматриваемом направлении, следующим образом:
Нт Н cos 6_ cos 6
Rb = — ------------------------------- - ■ (3.6.1)
Н НпСos ©z COS ©2
где cos ©т и cos ©r определяются с помощью соотношения (2.5.2).
В этом разделе кратко изложен расчетный метод из работы Хот - теля и Вёрпа [7], применимый для наклонных поверхностей:
COS ©_ cos (<р — s) COS б COS CO + sin (ф — s) sin Б
(3.6.2)
COS ©^ COS ф COS б COSC0 4- sin ф sin6
В расчетах можно непосредственно пользоваться либо уравнением (3.6.2), либо удобным графическим решением Хоттеля и Вёрца.
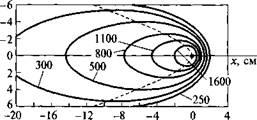
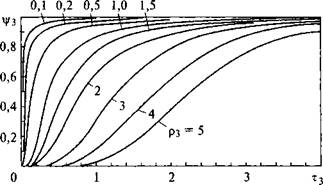
На фиг. 3.6.2 приведены графики зависимости cos ©т от склонения солнца и часа дня для интервала значений (ф - «) от 0 до 50°. Значения cos©z определяются по кривым, для которых (ф — s) равно широте местности. Величина cos©T находится по графикам с соответствующим значением (ф — s). Затем определяется отношение Rb. Величи - , ны cos©T, соответствующие отрицательным значениям (ф — s), определяются по кривым для положительных значений. При этом знак склонения меняется на обратный. График зависимости величины Rb от склонения при ф = 40° и s = 30° приведен на фиг. 3.6.3.
|
|
|
Склонение, град |
|
Фиг. 3.6.3. Отношение Rb = cos0T/cosez для поверхности с наклоном 30° к экватору на широте 40° для различных значений времени после полудня. |
|
-20 - ю о Ю го |
Пример 3.6.1. Пусть широта местности составляет 40°с. ш., а наклон поверхности к экватору 30°. Найти отношение Rb для
9.30 20 февраля. По фиг. 3.4.2 склонение равно -12°. В 9.30 величина со равна 37,5°. Так как (ф - s) составляет 10°, cos ©т, определенный по фиг. 3.6.2,6, равен 0,73, и, поскольку ф составляет 40°, cosвг, определенный по фиг. 3.6.2,е, равен 0,46. Отношение Rb тогда равно: 0,73/0,46 = 1,59. Такая же величина получается и по графику фиг. 3.6.3. Если воспользуемся уравнением
(3.6.2) , то получим
cos lOcos (—12)cos 37,5 + sin 10 sin (—12)
ft ------------------------------------------------------------- = 1,58.
cos 40cos (—12) cos 37,5 + sin 40sin (—12)