Основы ТЕХНОЛОГИИ МАШИНОСТРОЕНИЯ

Пространственные размерные цепи

Главный недостаток расчета плоских размерных цепей заключается в том, что линейные и угловые размерные цепи строятся как независимые и их расчет ведется независимо друг от друга [2]. В то же время деталь представляет собой совокупность поверхностей, образующих единое пространственное тело. Поэтому назначение допусков на расстояния и повороты поверхностей как на независимые величины, т. е. без их взаим­ного согласования, приводит к значительным ошибкам.

Ошибки начинаются уже с неточностей определения положения размеров. Например, показывая на чертеже детали (рис. 1.3.34, а), что плоскость Б должна быть параллельна плоскости А, не указываются ко­ординаты точки поворота плоскости Б и направление поворота. В резуль­тате при таком задании допуска на отклонение от параллельности воз­можны различные варианты фактического положения плоскости Б в пре­делах, заданных допуском, из-за разного положения точки 0 поворота поверхности; некоторые из этих вариантов показаны на рис. 1.3.34, в, г.

Если несколько таких деталей смонтированы в столбик (рис. 1.3.34, б), то при одних и тех же отклонениях от параллельности поверхностей ка­ждой детали, положение верхней плоскости столбика относительно ниж­ней плоскости при одном и том же допуске будет разным в зависимости от того, какое положение будут занимать детали.

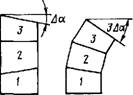
На рис. 1.3.34 д, е показаны два варианта сборки трех деталей с оди­наковыми угловыми погрешностями Да плоскости Б относительно плос­кости А. В первом случае (рис. 1.3.34, d) средняя деталь повернута при сборке на 180° таким образом, чтобы ее угловая погрешность была на­правлена в противоположную сторону угловым погрешностям двух дру­гих деталей. Тогда погрешность углового положения верхней плоскости столбика относительно основания равна Да.

Во втором случае (рис. 1.3.34, е) все угловые погрешности сложи­лись и погрешность углового положения верхней плоскости столбика относительно основания равна ЗДа.

Чтобы компенсировать эти недостатки при расчетах, ужесточают допуски, что приводит к росту расходов, связанных с достижением такой точности. Непрерывный рост норм точности изделий требует совершен­ствования методов расчета размерных цепей.

Из-за указанных недостатков расчеты линейных и угловых цепей в случаях, когда требования к точности высоки, носят ориентировочный характер. Отставание методов расчета на точность, основанных на пло­ской модели размерных цепей, известны давно. Основная тематика работ

О 1

8)

Рис. 1.3.34. Связи между размерами и поворотами поверхностей детали:

А - эскиз детали; б - сборочная единица из трех деталей; в - направление поворота поверхности Б, г - повороты поверхности Б при среднем положении точки 0; д - сборочная единица из деталей с разным направлением поворота поверхности Б', е - сборочная единица из деталей с одинаковым направлением поворота поверхности Б

По совершенствованию методов расчетов была направлена на развитие методов суммирования так называемых векторных погрешностей. Одна­ко недостатком таких решений являлось то, что и в этом случае за основу принималась плоская модель размерных цепей.

С целью повышения точности расчетов предлагается устанавливать и описывать размерные связи в машине с помощью пространственных размерных цепей. Наиболее полным решение задачи будет в том случае, если принять модель пространственной размерной цепи, базирующейся на известном положении теоретической механики, согласно которому положение твердого тела в пространстве описывается тремя линейными и тремя угловыми координатами. Такая модель отражает связи между линейными и угловыми размерами и

Их погрешностями. Я А

Рассмотрим построение про­странственной размерной цепи конст­рукции из двух столбиков, содержа­щих соответственно две и три детали (рис. 1.3.35), где замыкающим звеном является относительное положение поверхностей А и Б.

Упростим задачу, приняв в каче­стве замыкающего звена расстояние Рд

Между двумя точками поверхностей А и Б деталей 1 и 5 и построим коорди­натные системы на основных базах всех деталей (рис. 1.3.36).

Составляющими звеньями пространственной размерной цепи будут звенья, определяющие:

/ • положение поверхности А относительно комплекта основных баз детали /;

2 Положение комплектов основных баз детали 1 относительно комплекта основных баз детали 2:

3 - положение комплекта основных баз детали 2 относительно ком­плекта основных баз детали І;

4 Положение комплекта основных баз детали 5 относительно ком­плекта ее основных баз детали 4\

5 - положение поверхности Б относительно комплекта основных баз детали 5.

Как уже отмечалось, положение в пространстве одной детали отно­сительно другой можно определить тремя расстояниями и тремя поворо­тами, построив для этого на основных базах деталей прямоугольные сис­темы координат.

Основным понятием в теории размерных цепей является понятие звена, поэтому сформулируем понятие звена пространственной размер­ной цепи.

В постановке пространственной задачи звено пространственной размерной цепи должно отражать всю совокупность размерных связей, определяющих относительное положение двух геометрических элементов.

Такими геометрическими элементами могут быть сочетание поверх­ностей (например, комплект баз), поверхность, линия и точка.

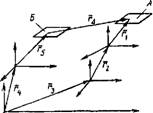
Пользуясь изложенным, для описания звеньев пространственной це­пи на комплектах основных и вспомогательных баз деталей должны быть построены прямоугольные системы координат, как это показано на рис. 1.3.35. Если теперь исключить из рисунка сами детали, то получим сово­купность координатных систем и поверхностей А и Б. Связав их радиус - векторами, получим пространственную размерную цепь (рис. 1.3.36). При рассмотрении относительного положения двух деталей звено простран­ственной размерной цепи должно отражать всю совокупность линейных и угловых размерных связей, определяющих относительное положение двух координатных систем. Тогда положение одной детали относительно другой можно определить с помощью радиус-вектора г, соединяющего начала координатных систем и матрицы трех поворотов М.

Соединив координатные системы радиус-векторами при условии, что ко­ординатные системы деталей 5 и 4 сов­падают, получим составляющие звенья пространственной размерной цепи (рис. 1.3.36):

H h r4 r5.

Итак, под звеном пространствен­ной размерной цепи будем понимать ра­диус-вектор и матрицу поворотов, опре­деляющих положение одного геометри­ческого элемента относительно другого.

Графически звено пространственной размерной цепи изображается ради­ус-вектором, соединяющим два геометрических элемента. В аналитиче­ской форме звено пространственной размерной цепи в общем случае представляется как

М = Мх, Mv, М.

Где х, у, z - координаты начала отсчета системы координат, положение которой определяется; Мх, Му, М._ - матрицы поворотов координатной системы последовательно вокруг осей X, Y, Z.

Если в качестве геометрических элементов выступает плоскость, линия или точка, то количество переменных в функциях Г --- fix, у, Z) и М =f(Mx, My, Mz) соответственно будет меньше.

В зависимости от постановки задачи возможны разные варианты аналитического выражения звена пространственной цепи. Его разнообра­зие определяется разновидностями геометрических элементов и их соче­таний, относительное положение которых надо найти.

Варианты сочетаний геометрических элементов образуются такими геометрическими элементами, как сложная пространственная поверх­ность, пространственная кривая, плоскость, плоская кривая, прямая и точка. Аналитическое описание звена пространственной цепи будет зави­сеть от образующих его геометрических элементов. Например, если зве­но образуют две сложные пространственные поверхности, то оно будет
описываться шестью характеристиками, а если звено образовано двумя точками, то оно будет описываться одной характеристикой - расстоянием между ними.

Таким образом, для описания относительного положения двух гео­метрических элементов каждого сочетания, образующего звено про­странственной размерной цепи, должно быть свое необходимое и доста­точное число характеристик.

Для описания звеньев, образованных сочетанием "сложная про­странственная поверхность - сложная пространственная поверхность", строятся координатные системы на обеих поверхностях и тогда их отно­сительное положение описывается тремя линейными и тремя угловыми размерами.

Для всех других сочетаний геометрических элементов надо положе­ние обоих элементов записать в системе координат, построенной на ос­новных базах любой из двух деталей, которым принадлежат геометриче­ские элементы, и записать их относительное положение в этой коорди­натной системе.

Таким образом, в зависимости от решаемой задачи точность замы­кающего звена может оцениваться по-разному.

В одном случае нужно учитывать отклонения всех параметров, ха­рактеризующих замыкающее звено, а в других случаях - только некото­рые из них. Пользуясь понятием звена пространственной цепи, можно сформулировать ее определение.

Под пространственной размерной цепью понимается совокупность радиус-векторов, образующих замкнутый контур и соединяющих геомет­рические элементы, которые непосредственно участвуют своим положе­нием в решении поставленной задачи.

Преимущество такого определения пространственной размерной цепи состоит в том, что в этом определении постулируется не только произвольный характер расположения звеньев в пространстве, но и про­странственный характер погрешностей.

В графической интерпретации пространственная размерная цепь бу­дет представлять собой замкнутый пространственный многоугольник, где его стороной является радиус-вектор, как это показана на рис. 1.3.36.

Определения замыкающего, составляющего, компенсирующего и общего звеньев сохраняют содержание, аналогичное звеньям плоских размерных цепей. Однако есть и отличия, вытекающие из определения звена пространственной размерной цепи.

Понятия увеличивающего и уменьшающего звеньев, используемые в теории плоских размерных цепей, теряют свой смысл, так как в случае пространственной размерной цепи одни характеристики составляющего звена при их изменении могут увеличивать характеристики замыкающего звена, а другие - уменьшать. Таким образом, можно лишь говорить о ха­рактере влияния изменения каждой из характеристик составляющего зве­на на значение той или иной характеристики замыкающего звена.

Понятия, приведенные в теории плоских размерных цепей, опреде­ляющие такие виды размерных цепей, как основная, производная, конст­рукторская, технологическая, измерительная, а также параллельно свя­занные, последовательно связанные, комбинированные размерные цепи, сохраняются и для пространственных размерных цепей.

Понятия линейной, угловой и плоской размерных цепей, как зто сформулировано в теории плоских размерных цепей, теряют свой смысл в связи с пространственной постановкой задачи.

При расчете пространственных размерных цепей так же, как и ли­нейных, решаются прямая и обратная задачи. При решении прямой зада­чи, исходя из установленных требований к точности замыкающего звена, определяют номинальные значения каждого из шести параметров, поля допусков, координаты середин полей допусков и предельные отклонения по каждому из параметров каждого составляющего звена.

При решении обратной задачи, исходя из установленных номи­нальных значений, полей допусков и координат середин полей допусков, по каждому параметру на каждое составляющее звено определяются но­минальное значение, поле допуска, координаты середины поля допуска и предельные отклонения по каждому параметру замыкающего звена.

Принципиальное отличие расчета пространственной размерной цепи от линейной и угловой заключается в том, что номиналы и допуски на линейные параметры х, у, z и угловые ф, 0 рассматриваются как взаи­мосвязанные величины.

Если при решении прямой задачи линейной размерной цепи недос­тает нужного числа уравнений для определения числовых характеристик составляющих звеньев, то для пространственной размерной цепи этот недостаток усугубляется в еще большей степени из-за того, что увеличи­вается число переменных. Одной из важнейших задач в развитии теории пространственных размерных цепей и является разработка методов ре­шения прямой задачи.

В решениях прямой и обратной задач сохраняются два принци­пиально отличных направления: расчет на максимум-минимум и веро­ятностный расчет. Первое направление применяется, когда требуется обеспечить 100 %-ю взаимозаменяемость изделий, второе направление
применяется, когда допускается определенная доля изделий, у которых возможно превышение отклонения замыкающего звена над его допуском.

Теорией и практикой применения плоских размерных цепей разра­ботаны пять методов достижения точности замыкающего звена; все они по своему содержанию остаются справедливыми и для пространственных размерных цепей, однако расчетные формулы будут другими.

Основой методов расчета замыкающего звена является уравнение радиус-вектора как функции радиус-векторов и матриц поворотов со­ставляющих звеньев. Оно содержит радиус-векторы Л,, определяющие положение начал координатных систем и матрицы М\ трех поворотов каждой координатной системы, последовательно вокруг каждой коорди­натной оси, т. е.

Где /д - радиус-вектор замыкающего звена; Л4 - матрица поворотов за­мыкающего звена; т - число звеньев в размерной цепи. В обобщенном виде уравнение имеет вид:

Где п - порядковый номер составляющего звена: ri - радиус-вектор г-го составляющего звена; М\ - матрица поворотов или матрица направляю­щих конусов г-й координатной системы относительно базовой (г - 1)-й координатной системы.

Матрица М\ вычисляется по следующей формуле:

Cos i|cos 0, sin ф,- sin у,- cos 8,- - sin у,- cos ф,- cos В,- +

- sin 8,- cos ф,- Ml = sin 0,- cos sin ф,- sin sin 0, +

+ cos ф,- cos8,- -sin\(y; sin Ф,-COS