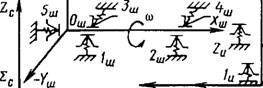Основы ТЕХНОЛОГИИ МАШИНОСТРОЕНИЯ

ПОСТРОЕНИЕ МОДЕЛИ ФОРМИРОВАНИЯ ГЕОМЕТРИИ ДЕТАЛИ МЕТОДОМ КООРДИНАТНЫХ СИСТЕМ С ДЕФОРМИРУЮЩИМИСЯ СВЯЗЯМИ

При построении модели необходимо, чтобы она отражала описы ваемый процесс с требуемой точностью и в то же время была максималі. но простой. Часто под критерием простоты модели понимается наймеш, шая трудоемкость вычислений с ее помощью.

Между двумя указанными требованиями имеет место противоречие: с одной стороны: необходимо повысить точность расчетов, а с другой стороны - упростить модель. Структура модели обусловлена задачей. Математические модели могут описывать разные стороны технологиче­ского процесса. Чем более полно модель отражает этот процесс, тем она точнее и более широкий круг задач может быть решен.

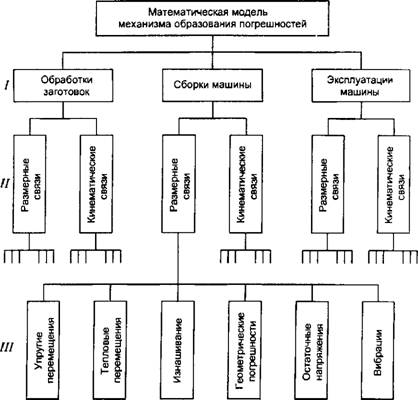
Чтобы избежать ненужной сложности модели и неоправданного увеличения трудоемкости расчетов, необходимо строить в каждом случае такую модель, которая позволяла бы решать только поставленную зада­чу. Модели (рис. 1.8.3), описывающие механизм формирования геомет­рии изделия, могут быть трех уровней.

На первом уровне модели различают по типу процесса. На втором уровне модели описывают погрешности, обусловленные погрешностями размерных и кинематических связей. В модели третьего уровня включа­ют действующие факторы и соответствующие характеристики качества машины, препятствующие вредному влиянию этих факторов.

Независимо от того, какую модель из приведенной классификации будут разрабатывать, ее построение имеет следующие этапы: постановка задачи; построение эквивалентной схемы; вывод уравнения относитель­ного движения рабочих поверхностей; составление уравнения движения с учетом факторов, нарушающих заданный ход технологического процес­са; проверка модели на адекватность.

В основу построения модели методом координатных систем с де­формирующимися связями положены причинно-следственные связи ме­ханизма образования погрешностей изготовления детали (рис. 1.8.4). Рас смотрим содержание этапов построения модели.

Постановка задачи. Построение модели прежде всего предполагает выбор критерия оценки результата процесса. При обработке на станке заготовка должна приобрести геометрию детали с отклонениями, не пре­вышающими границ, заданных допуском.

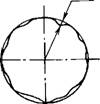
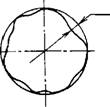
Как известно, точность детали принято характеризовать точностью линейных и угловых размеров и формы поверхностей детали. При этом известные методы и критерии оценки по каждому из перечисленных по казателей приводят к обезличиванию факторов, влияющих на погреш ность обработки. На рис. 1.8.5 показаны два разных профиля поперечных сечений реального вала. С помощью известной методики оценки по грешности формы отклонение от круглости определяется как максималь ное отклонение точки профиля от прилегающей окружности. При таком методе оценки круглости у двух разных по форме поперечных сечений величины отклонений могут оказаться одинаковыми. Это подчеркивает

6)

Рис. 1.8.5. Отклонение от круглости вала в поперечных сечениях:

А, б - профили поперечного сечения вала соответственно при отклонении А, и А?

То, что при такой оценке погрешности утрачивается непосредственная связь между искажением формы профиля и фактором, его порождающим.

С другой стороны, точность одной и той же по форме детали оцени­вают по разным методам - в зависимости от ее служебного назначения. Например, отклонение от круглости поперечного сечения цилиндриче­ского вала можно определять как отклонение от прилегающей окружно­сти, так и от средней окружности, построенной из условия миним\ма суммы квадратов отклонений точек профиля. В итоге оценка точное і и одного и того же профиля окажется разной.

Аналогично по-разному оценивается точность детали и по другим показателям - размеру и относительному повороту поверхностей дет али.

Таким образом, точность одной и той же детали, но разного служеб­ного назначения будет разной. Наличие такой неоднозначности не позво­ляет выбрать погрешность детали в качестве критерия погрешности об­работки. Учитывая изложенное, следует различать понятия погрешноеп. обработки и погрешность детали.

Под погрешностью детали будем понимать отклонение от заданных линейных и угловых размеров, формы ее поверхностей, определяемых по известным методикам в соответствии со служебным назначением детали.

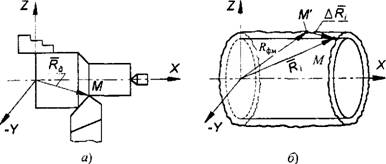
Чтобы сформулировать понятие погрешности обработки, обратимся к схеме (рис. 1.8.6, а) токарной обработки заготовки. Каждая точка обра­ботанной поверхности формируется соответствующими точками режу­щих кромок лезвия резца в соответствующий момент времени в системе отсчета, построенной на технологических базах заготовки.

Поэтому под погрешностью обработки условимся понимать откло­нения ДЯ, фактического радиуса-вектора ДЯф, й точки обработанной

Поверхности детали от заданного R,, отсчитанные в j-Pi момент времени обработки в системе координат, построенной на технологических базах детали. Согласно рис. 1.8.6, б

ДR, = ДЛф, - R,.

Преимуществом такой оценки погрешности обработки является одно­значность ее определения при действии любого рассматриваемого фактора в любой точке обработанной поверхности детали. Это позволяет устанавли­вать влияние действия каждого фактора на погрешность обработки.

К сожалению, в многочисленных исследованиях, посвященных изу­чению влияния различных факторов, устанавливались зависимости меж­ду действующим фактором и не погрешностью обработки AR,, а по­грешностью детали, определяемой по конкретной методике. В итоге по­лученные результаты оказывались справедливыми только для выбранной методики оценки точности детали. Поэтому полученные зависимости нельзя было экстраполировать на случаи оценки точности по другим ме­тодикам, в результате полученные зависимости приобретали частный характер.

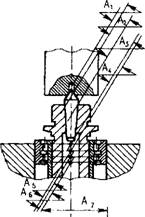
Построение эквивалентной схемы. При обработке на станке заго­товка включается в размерные и кинематические цепи технологической системы в качестве замыкающих звеньев. Согласно уравнению размер­ной цепи, погрешность обработки в любой точке детали будет равна ал гебраической сумме погрешностей составляющих звеньев размерной не пи. Так, в размерной цепи токарного станка (рис. 1.8.7, а) замыкающим звеном является расстояние между вершиной лезвия резца и осью вала. В этом случае ось вала совпала с осью координатной системы, построен­ной на технологических базах заготовки.

В соответствии с методом координатных систем с деформирующи­мися связями для построения эквивалентной схемы на основных базах деталей, размеры которых вошли в размерную цепь как составляющие звенья, строят системы прямоугольных координат. Построение каждой системы координат начинается с определения схемы базирования каждой из этих деталей.

Если детали оставляют одну или несколько степеней свободы, то число опорных точек в схеме базирования будет меньше шести и може і получиться неполный комплект основных баз. В этом случае, построим координатные плоскости на имеющихся поверхностях основных баз, не обходимо достроить координатную систему, проведя недостающие коор­динатные плоскости.

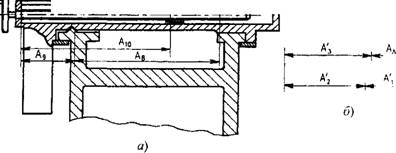
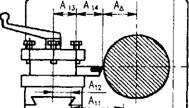
Часто число деталей, вошедших своими размерами в размерную цепь, бывает значительным. Это приводит к большому числу координат ных систем в эквивалентной схеме и, как следствие, громоздкости мате матических выражений и значительному повышению трудоемкости вы числений; поэтому необходимо стремиться к уменьшению числа коорди­натных систем в эквивалентной схеме. Это возможно в результате по строения координатных систем на поверхностях основных баз сборочных единиц. Тогда размерную цепь строят из приведенных звеньев, в которой каждое приведенное составляющее звено представляет собой замыкаю щее звено группы звеньев.

В примере токарного станка (рис. 1.8.7, б) составляющие звенья размерной цепи можно объединить в группы: патрон - шпиндель - пе редняя бабка; резец - суппорт - поперечные и продольные салазки. Тогда размерная цепь будет содержать только четыре звена (см. рис. 1.8.7, 6) Ад, А\, А'2, А'з - отражающие размерные связи между заготовкой, шпин дельной, суппортной фуппами и станиной.

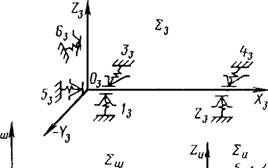
Чтобы в эквивалентной схеме учесть кинематику технологической системы, в координатных системах, построенных на деталях с заранее обусловленным наличием степеней свободы, указывают заданное движе ния (поступательное или вращательное). В соответствии с изложенным на рис. 1.8.8 показана эквивалентная схема технологической системы токарного станка для случая с приведенными звеньями, в которой за не подвижную систему принята система Ес, построенная на направляющих станины, а на технологических базах заготовки построена координатная система Е3, а 1ш, £и построены соответственно на основных базах шпин деля и инструмента. Система 1ш имеет вращательное движение (ш), ;i система £и - поступательное (S ).

/

Рис. 1.8.8. Эквивалентная схема технологической системы токарного станка:

£и, £с - координатные системы соответственно заготовки, инструмента с суппортной группой, шпинделя, станины

В тех случаях, когда необходимо раскрыть механизм формирования погрешности обработки, обусловленной отклонениями звеньев кинема­тических цепей, следует ввести дополнительные построения. С этой це­лью определяют кинематическую цепь, устанавливают схему базирова­ния каждого элемента кинематической цепи и на поверхностях основных баз этих элементов строят координатные системы [2].

Вывод уравнения относительного движения режущих кромок инструмента и технологических баз заготовки. Чтобы определить по­грешность обработки Ав і-й точке полученной поверхности обрабо­танной детали, следует решить уравнение относительного движения ре­жущих кромок инструмента и технологических баз.

Запишем уравнение движения на примере токарной обработки Пусть резец совершает поступательное движение, а заготовка вращается (рис. 1.8.9). Тогда в неподвижной координатной системе £3 заготовки резец будет совершать винтовое движение. Задача сводится к тому, что­бы определить А Л, в любой момент обработки. Если говорить строго, то необходимо записать уравнение движения режущих кромок лезвия, фор­мирующих поверхность вала. Для упрощения изложения вопроса запи­шем уравнение движения одной из точек режущих кромок, например вершины лезвия (точка М).

Согласно схеме (см. рис. 1.8.9), уравнение движения точки Мв сис­теме S3 будет иметь вид:

= /i(*„> Уи> 2и> 0;

' Уз ую z„, t)\ (1.8.1)

Л =/з(*и> Уи> ги> 0,

Где jc„ уъ, z3 - координаты точки М в координатной системе £3 заготовки. хи, ун, z„ - координаты точки М в координатной системе S„ резца; t - па раметр движения (время, угол поворота и др.).

При обработке заготовки происходит изменение относительного по ложения систем £3 и Еи, поэтому и значения хг, уъ, z3 будут изменяться.

Чтобы записать уравнение фактического движения точки М в систе­ме 23, необходимо в правую часть уравнения (1.8.1) в качестве аргумен­тов включить величины, характеризующие каждый блок схемы, приве­денной на рис. 1.8.4. Согласно этой схеме, нарушение относительного движения является следствием дополнительных перемещений и поворо­тов координатных систем эквивалентной схемы (см. рис. 1.8.8).

Чтобы уравнение движения (1.8.1) отражало перемещения и поворо­ты координатных систем 13, £и эквивалентной схемы в неподвижной системе 1с, следует в его правую часть включить характеристики, опре­деляющие положение каждой координатной системы.

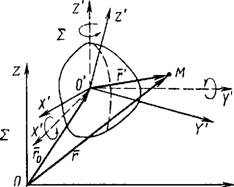
Известно, что положение твердого тела в пространстве относитель­но неподвижной системы координат L может быть определено с помо­щью шести параметров: трех угловых и трех линейных координат систе­мы координат I', жестко связанной с этим телом (рис. 1.8.10). Таким об­разом, положение детали в системе координат I может быть определено с помощью радиус-вектора г и матрицы углов поворотов:

Г0= у0 • М = М^уМІУі V)-M(z,0), z0

Где х, у, z — координаты начала системы координат I' в системе S; М(х, ф), Л/(г, в) - матрицы поворотов против часовой стрелки системы коор­динат 2' соответственно на угол <р вокруг оси ОХ\ на угол у вокруг оси ОТ' и на угол 0 вокруг оси <7Z'.

Введем в правую часть уравнения движения (1.8.1) параметры, оп­ределяющие положения каждой координатной системы эквивалентной схемы. Это выполняют с помощью формул перехода из одной системы координат в другую.

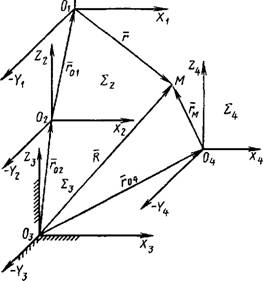
В совокупности координатных систем эквивалентной схемы, где = 2Ь = Е2. ^с = и Хи = Х4 за неподвижную систему координат примем (рис. 1.8.11). Соединив начала координатных систем радиус - векторами, можно записать два векторных равенства:

R = г02 + roi + П

R - г04 +гм.

Z,

Приравняв правые части равенств (1.8.2) и (1.8.3), получим уравне­ние радиус-вектора F, определяющее положение точки М в системе Јt:

? = ~Ца(1.8.4)

Пользуясь формулами перехода из одной координатной системы в другую, найдем последовательно положение точки М в координатных системах Е3, 12> С этой целью запишем формулы перехода, для чего найдем положение точки М координатной системы 2' в системе 2 (рис. 1.8.12) при их параллельном положении. Уравнения координат точ­ки М в системе X будут иметь следующий вид:

X ~~ Xq + Xі J

У =>"0 +У' или r=r0 + F';

Z = z0 + z',

Где х', у', z' - координаты точки М в системе Г; х0, у0, z0 - координаты точки 0' в системе

В общем случае система Xі может быть непараллельна системе I, то­гда в формулу перехода должны быть включены углы ее поворотов. Пусть точка М задана в системе Г; надо определить ее положение в сис­теме

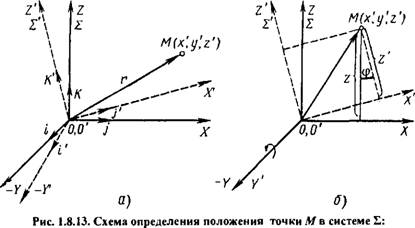
Пусть система 2' повернута в пространстве так, что ее оси будут не­параллельны осям системы 2 (рис. 1.8.13, а), при этом начала систем Ъ и Е' совпадают.

При повернутой системе Е' положение точки М в системе Е опреде­ляется радиус-вектором

Г = М'г\

Где М' - матрица поворота системы Е' в системе Е; г - радиус-вектор, определяющий положение точки М в системе Е\

В этом случае формула перехода точки М из системы Е' в систему Е будет иметь вид

X = cos (і і')х' + cos(/ j')y + cos(/ k')z'\

/S

Y = cos(l j')x' + cos(j j')y' + cos(j k')z'\ (1.8.5)

■Л. ^

Z = cos(k i')x' + cos(k j')y' + cos(k k')z', где cos(//'), cos(/ j'),..., cos{k к') - косинусы углов (направляющие коси­нусы) между осями систем Е и Е', i, j, к - единичные векторы.

Влияние поворота системы 2' на положение точки М в системе I от­ражено через направляющие косинусы. С целью сокращения записи вве­дем обозначения направляющих косинусов через и,:

Cos(//') = "n; cosO'/) = m12; cos{ік') = щг\

Cos0V) = и21; cos(J]') = и22; cos(Jк') = u2i;

Cos(Ј /') = и31; cos(X/) = и32; cos (кк') = игъ.

Тогда формула перехода (1.8.5) будет иметь

Запишем формулы перехода точки М из координатной системы X' в координатную систему Ъ при последовательном повороте системы I' во­круг осей OX, OY, OZ, при условии, что начала координатных систем X и Е' совпадают.

На рис. 1.8.13, б показано положение системы Т после ее поворота вокруг оси ОД" на угол ср против часовой стрелки.

Уравнения координат точки М в системе £ будут иметь следующий

Вид:

Х = х'\ + у'О + z'O; у - х'О + у' cos ф + z'(- sin ф); z = х'0 + у' sin ф + z' cos ф,

Или

Х = х;

У = /соэф - г'зіпф; z = /зіпф + г'созф.

Матрица поворота системы Е' вокруг оси ОХ на угол ф имеет вид

1 О О

О соэф — sin ф. (1.8.6)

О sin ф cos ф

Аналогичным образом можно записать матрицы поворотов системы 2' вокруг других осей.

Уравнение координат точки М в системе 2, когда система 2' повер­нута на угол \|/ вокруг оси О Y:

Х = х cos ці - z smiy;

У = У;

Z = - x'sin ці + z'cosv(/.

Отсюда

COS V 0 - sin ЦІ

О 1 О

Sin ЦІ О COS ЦІ

Уравнение координат точки М в системе 2, когда система 2' повер­нута на угол 0 вокруг оси OZ:

X - x' cos 0 + y'(-sin 0); >' = x'sin0 + >''(cos0); z =z'.

Отсюда

Cos 0 - sin 0 0 sin0 COS0 0 0 0 1

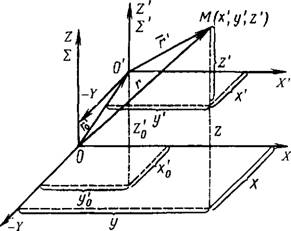
В обшем случае, когда система 2' повернута относительно системы 2 и их начала не совпадают, радиус-вектор точки А/, определяющий ее положение в системе 2, будет иметь следующее выражение:

Г =r0 + Mr',

Где F0 - радиус-вектор, определяющий положение начала координат сис­темы 2' в системе 2.

Пользуясь формулами перехода (1.8.5) - (1.8.8) из одной координат­ной системы в другую, запишем уравнение радиус-вектора F, опреде­ляющего положение точки М в координатной системе 2], эквивалентной схемы (см. рис. 1.8.11).

С этой целью вернемся к равенству (1.8.4) и запишем значение R с учетом поворотов координатных систем 2,, 22, 24 в системе 23.

Положение точки М в системе 2| (см. рис. 1.8.11) определяется ра­диус-вектором R, уравнение которого имеет вид

R =rM +/V/4Fm. (1.8.9)

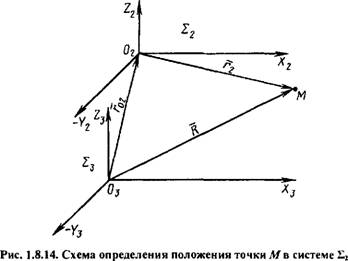
Положение точки М в системе 22 (рис. 1.8.14) определяется радиус - вектором г2, уравнение которого найдем следующим образом. Вначале

Запишем уравнение радиус-вектора R, считая, что положение точки М в системе 22 известно, тогда

R=F02+M272. (1.8.10)

Или

М2гг =R - F02,

Откуда

F2 = M2\R-F02). (1.8.11)

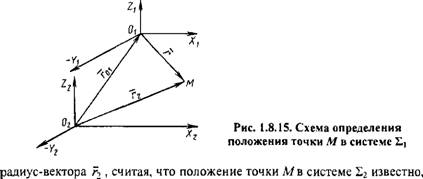
Теперь найдем положение точки М в системе Еі (рис. 1.8.15); ее по­ложение определяется радиус-вектором F. Сначала запишем уравнение

Или M\F = r2-rm. (1.8.12)

Подставим в выражение (1.8.12) значение гг: Mxr = M2(R-r02)-r0].

В полученное выражение подставим значение R

М^ = М2\М4гм +rM-г02)-?01. (1.8.13)

Проведя преобразования, получим уравнение (1.8.13) следующего

Вида:

Г = М-][м-2](М4г4-гм-г02)-г01]. (1.8.14)

Уравнение (1.8.14) позволяет определить координаты точки полу­чаемой поверхности детали.

Чтобы определить все точки поверхности, надо в (1.8.14) ввести па­раметры движения координатных систем в соответствии с кинематикой станка. Например, у токарного станка, эквивалентная схема которого по­казана на рис. 1.8.8, в соответствии с его кинематической схемой коорди­натная система имеет вращательное движение вокруг оси ОХш, а коор­динатная система £и - поступательное движение вдоль оси ОХи.

С помощью уравнения (1.8.14) можно учесть перемещения и пово­роты координатных систем эквивалентной схемы, вызванные действую­щими факторами.

Учет факторов, порождающих погрешности обработки. Для уче­та влияния действующих факторов на погрешность обработки вначале необходимо ввести в полученное уравнение движения (1.8.14) перемеще­ния опорных точек.

В результате действия факторов (см. рис. 1.8.4) возникают погрешности обработки, которые можно выразить через перемещения опорных точек ко­ординатных систем. В свою очередь перемещения опорных точек создают перемещения и повороты координат­ных систем. Поэтому сначала необхо­димо установить аналитические зави­симости трех перемещений и трех по­воротов координатной системы от пе­ремещения опорных точек. Иными сло­вами, в уравнение движения (1.8.14) вместо г, и М, должны быть введены их функции от перемещений опорных то­чек. Эти зависимости находят из геометрических соотношений. Напри­мер, выведем указанную зависимость для системы 2) (рис. 1.8.16), задан­ной в системе 2. Координаты опорных точек в системах 2| и 2 приведены в табл. 1.8.1.

Давая перемещения X опорным точкам в координатной системе 2 в направлении лишения ими соответствующих степеней свободы, с помо­щью геометрических соотношений найдем значения отклонений шести

Координат, определяющих новое положение координатной системы 2( в системе 2. Для варианта расположения опорных точек (см. рис. 1.8.16) зависимости имеют следующий вид:

Х = К5; у = ХЪ + jrntg0; z = A,, +jcntgv|/;

Cp = A.6/z,; v)/ = arctg 0 = arctg

4jc21 - xu

Где X\ - Хб - перемещения опорных точек.

В уравнение движения вместо координат х, у, z, ср 0 радиус - векторов и матриц подставляют правые части зависимостей (1.8.15), свя­зывающие перемещения опорных точек с шестью координатами. Следует оговориться, что для другой схемы расположения опорных точек зависи­мости (1.8.15) будут другими.

Теперь, чтобы ввести в уравнение движения фактор, порождающий от­клонения движения точки М в координатной системе 2] (см. рис. 1.8.11), необходимо перемещения ki каждой опорной точки представить функци­ей этого фактора. Например (рис. 1.8.17), упругое перемещение X, опор­ной точки детали системы можно представить как функцию ее жестко­сти, тогда

"b-yi - I Jji

Где Л,- - реакция в г'-й опорной точке от всех сил и моментов, действую­щих на деталь этой координатной системы; j - жесткость г'-й опорной точки.

Чтобы найти реакции в опорных точках, составляют шесть уравнений равновесия статики: 2Рх = 0; 2Ру = 0; 2Р2 = 0; 1МХ = 0; IMY= 0; IM? = 0.

Жесткость детали в опорных точках рассчитывают или определяют экспериментально. Аналогичным образом включают в уравнение движе­ния другие факторы, такие, как тепловые перемещения, износ, остаточ­ные напряжения, представляя их через перемещения опорных точек. Подставив в уравнение движения (1.8.14) вместо перемещений опорных точек их функции и введя ограничения на переменные в правой части уравнения, получим математическую модель механизма образования геометрических погрешностей.

В заключение надо отметить следующее. Обработка деталей на станках отличается большим разнообразием методов обработки (точение, растачивание, фрезерование, шлифование, сверление, протягивание и др.) режущего инструмента, приспособлений. Все это влияет на характер ме­ханизма образования погрешностей обработки, обусловливает действие тех или иных факторов, доминирование каких-либо из них. Иными сло­вами, в каждом конкретном случае имеется определенная специфика ме­ханизма образования погрешностей обработки.

Отсутствие единого подхода к построению модели механизма обра­зования погрешностей обработки породило бесчисленное множество его экспериментальных исследований. На основе этих исследований разра­ботано большое число моделей вероятностно-статистического вида, что не позволяет перейти к существенным обобщениям и в каждом конкрет­ном случае требует построения очередной модели.

Метод координатных систем с деформирующимися связями откры­вает возможность единого подхода к построению моделей механизма образования погрешностей независимо от метода обработки, типа метал­лорежущего оборудования, режущего инструмента и приспособления.

Проверка модели на адекватность. Успех применения построен­ной математической модели для решения задач во многом зависит от степени ее адекватности реальному объекту. Необходимость проверки модели на адекватность объясняется тем, что любая модель всегда лишь с некоторым приближением описывает поведение реального объекта, так как при принятой идеализации оригинала некоторые его стороны и ха­рактеристики оказываются неучтенными.

В задачу проверки модели на адекватность входит сопоставление ее выходных переменных с выходными переменными реального объекта при одних и тех же входных воздействиях

Если в ходе проверки модели на адекватность ошибки, характери­зующие точность модели, превосходят ошибки наблюдений, то гипотеза об адекватности модели отклоняется.

Действительные значения выходных переменных реального объекта остаются неизвестными, и сопоставление выходных данных модели про­изводится с наблюдаемыми значениями выходных данных реального объекта. Поэтому установленная степень соответствия модели реальному объекту будет зависеть не только от точности модели, но и от ошибок измерения выходных данных реального объекта.

Поскольку при построении математической модели реального объ­екта не принимаются во внимание те или иные стороны последнего, по­стольку эта модель будет описывать поведение объекта с требуемой точ­ностью лишь в какой-то определенной области, ограниченной значения­ми параметров процесса и значениями характеристик объекта.

В связи с изложенным, проверка модели на адекватность требует решения трех задач: определение требуемой точности модели, определе­ние области, в которой модель обязана "работать" с заданной точностью; разработка методики экспериментального исследования, обеспечиваю­щая получение результатов наблюдений в минимально необходимом объеме с погрешностью в пределах допуска.

Точность модели. Под точностью модели будем понимать степень приближения расчетной величины выходного параметра его наблюдае­мому значению. В рассматриваемом случае это будет степень приближе­ния расчетного значения радиус-вектора Rf в г'-й точке поверхности де­тали измеренному в R" этой же точке. Разница Лгр -R" = AR" будет определять погрешность модели в г'-й точке, однако в другой точке по­верхности детали эта разница может быть иной. Поэтому оценивать точ­ность модели надо в совокупности точек поверхности детали.

Пользуясь общепринятыми рекомендациями, допуск на отклонение ДR" следует устанавливать из расчета 10 % от допуска на точность рас­чета Л,-.

Область применения модели. Ме­ханизм образования геометрических погрешностей машины может быть "очерчен" многомерной областью диа­пазонов изменения факторов, порож­дающих эти погрешности (рис. 1.8.18).

Проверяемая на адекватность мо­дель всегда включает лишь часть этих факторов. Следовательно, многомер­ность области модели всегда меньше и будет определяться составом факторов, вошедших в правую часть уравнения относительного движения. Поэтому не­правомерно сопоставление выходных показателей модели с выходными пока­зателями реального объекта в любой точке области последнего. Сопоставле­ние нужно проводить только в тех точках, которые принадлежат одно­временно областям модели и реального объекта. Например, если прове­ряется на адекватность модель механизма образования упругих переме­щений элементов машины, то за геометрическую погрешность принима­ют только ту ее часть, которая образуется упругими перемещениями. В этом случае область модели будет описываться диапазонами изменения силы и жесткости. По мере включения в модель других факторов область ее применения расширяется. Определив область действия модели, следу­ет установить число точек, в которых будет осуществляться проверка на адекватность. С этой целью диапазон изменения фактора разбивается на интервалы. Проверка модели во всех установленных точках позволит выявить область, в которой точность модели соответствует заданной.

Экспериментальное исследование реального объекта. Большое зна­чение для проверки модели на адекватность имеет тщательность прове­дения экспериментального исследования. Однако проведение экспери­ментальных исследований с охватом всех точек, как правило, отличается высокой трудоемкостью и длительностью. В связи с этим целесообразно при планировании эксперимента отказаться от полного факторного экс­перимента. Тогда проверка модели на адекватность будет сведена к со-
поставленню ее выходных данных с выходными данными статистической модели, построенной на основе экспериментальных исследований.

При проведении экспериментальных исследований механизма обра­зования геометрических погрешностей имеют место некоторые специфи­ческие особенности, на которых целесообразно остановиться. При прове­дении экспериментального исследования вызывает затруднение опреде­ление жесткостей опорных точек каждой детали, вошедшей в эквива­лентную схему. Сложность решения этой задачи заключается в том, что затруднен доступ к местам контакта сопрягаемых поверхностей деталей.

Эту задачу решают двумя путями. Первый путь заключается в опре­делении суммарной жесткости нескольких деталей (сборочной единицы) с последующим равномерным распределением этой жесткости по дета­лям. Такой путь допустим, когда детали, вошедшие в эту сборочную едини­цу, сходны по конструктивным признакам и схеме нагружения.

В тех случаях, когда указанное усреднение значений жесткостей не удовлетворяет требованиям к точности определения жесткостей опорных точек, переходят к экспериментальному определению жесткости в каж­дой опорной точке - второй путь. С этой целью определяют расположе­ние точек (пятен) контакта сопрягаемых поверхностей; число таких точек определяет число степеней свободы, лишаемых данной базой.

При соприкосновении реальных поверхностей из-за наличия их гео­метрических отклонений расположение точек контакта является случай­ным, поэтому вынуждены задаваться расположением опорных точек ап­риори.

Поскольку, как правило, непосредственный доступ к измерению пе­ремещений этих опорных точек в направлении лишения ими степеней свободы невозможен, вынуждены их перемещения определять пересчетом.

В основу методики пересчета положено условие, что деталь пред­ставляет собой абсолютно твердое тело. Поэтому, зная координаты опор­ных точек в координатной системе исследуемой детали, достаточно оп­ределить перемещения в любых выбранных точках, где это позволяет конструкция детали, а затем пересчетом определить перемещения детали в опорных точках.

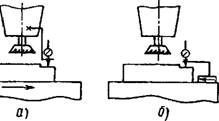
Другая задача, которая решается при проведении экспериментально­го исследования - это измерение геометрических погрешностей; особое значение она приобретает при исследовании механизма образования по­грешностей обработки. Например, при исследовании погрешности обра­ботки, обусловленной упругими перемещениями элементов технологиче­ской системы, надо уметь выделить и рассчитать только ту часть

Погрешности, которая образована упругими перемещениями элементов технологической системы. С этой целью рекомендуется перед обработ­кой детали подготовить измерительную базу. Для этого методом "выха­живания", т. е. в несколько проходов, без изменения статической на­стройки осуществляют обработку небольшой части той поверхности, которая должна быть обработана. После этого обрабатывают всю по­верхность, затем определяют отклонение точек обработанной поверхно­сти от измерительной базы и их отклонения рассматривают как результат упругих перемещений элементов технологической системы, имевших место во время обработки.

Немаловажное значение имеет и выбор базы установки измеритель­ного устройства. На рис. 1.8.19 показаны два варианта установки индика­тора. В первом случае (рис. 1.8.19, а) в измерение не будет включаться погрешность обработки от геометрической неточности поверхности стола.