Механика трубопроводов и шлангов

Аэродинамические силы, действующие па движущийся стержень

Основные соотношения. Рассмотрим силы, действующие иа стержень круглого поперечного сечения, считая, что имеет место квазистационарное обтекание стержня потоком Считаем, что изменение угла атаки приводит к мгновенному изменению аэро­динамических енл до значений, соответствующих новому углу атаки. Поток обладает инерцией, и поэтому изменение аэроди­намических сил происходит не мгновенно, а в течение некоторо­го времени, поэтому предположение о мгновенном изменении сил может только усилить эффект действия аэродинамических сил на конструкцию, т. с. идет в запас прочности конструкции.

Выведем формулы для аэродинамических сил, действующих на движущийся стержень.

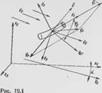
В гл. III были получены выражения для распределенных аэродинамических сил, действующих на покоящийся в потоке стержень. При движении стержня аэродинамическая сила зави­сит от относительной скорости (рис. 19.1).

®от=*и0 —w (s, т), (19Л)

Гте и (е, т) — вектор скорости точек осевой линии стержня. В статике относительная скорость совпадает с абсолютной ско­ростью потока о п.

Вектор

YOT=vh [( cos а — %uV() iY — 4-( sin a—, /3,)j (19.2)

Lpt1 .

Uxt —Сезразмер-

И ые скорости.

В соответствии с принятым допущением, что нормальная и касательная составляющие за­висят соответственно от квад­рата проекции относительной скорости на направление нор­мали и на направление каса­тельной к осевой линии стерж­ня. имеем (в безразмерной форме)

(19.3)

При движении стержня <j:;; — угол между векторами < 1 II У от, поэтому

(®от)л = г1от sin Vg> (4,J' = ®OTCOSUJg, (19.4)

Где

(PoT-ei) OD

(19.5)

Sin 9^ — 1 1 — cos2 tps;

|®bJ=®oV (cosa — ?0«J(,)2 +t&i, + (siiia — Р0«*,)2. (19-6)

Определение компонент вектора qn в неподвижных осях. Вектор, как и в статике, должен удовлетворять условиям

(чJ)2 = ?L, + <Ux, + ?L-.= - e„pd®o, sin2 o^2;

+ ?«*, + ?„д-„ *з=0;

Чп Ьот X ej = (д„ с) = qnXtcl -[- ?№c2+0„,ci=O. fi = (ЧпХч-Кз — (,о1Л).г, да;

=(®or).<,-*! — Юл*;

(®or)-f i= ®ov V, = (CoS a — ?0H-i.) ’

Vmx±=-yixa; (19.11)

‘zw,=*a0 (sin a— fJ0«jfS)-

Входящие в уравнения (19.10) х/ можно представить в виде

Xi—XiQ--uXi, (19.12)

Где x'io — направляющие косинусы вектора ё10 в статике; u'Xi—

Изменения величии направляющих косинусов, вызванные движе­нием стержня.

Из системы (19.8) — (19.9) находим qnXl и q, lXi в зависимо­сти от дпх,‘

7«,= -?«. f, ?«.= -?«, f-, (19.13)

Где

Д j = с2хз — сус2; Д2=— ^лгз; Д3=с2Л'1 — с 1X2. (19.14)

Из уравнения (19.7) находим

9по(^)2 S^Vg-3 , c„fdvp

Щ ■ (19.15)

У Д* + д| + Д* V 2Л33

SinS^.Ax? йо(—) Sin2 (fg‘ Д2

____ „ „ ____________

И <7„.Г2 =--------

(19.16)

Где 0=ГДі+ Д2 —А^. (19.17)

Преобразуем выражения для В введя вектор А с компонента­ми, равными Аг - (19.14). Вектор А можно представить как век­торное произведение вектора с на вектор ё\

Д=схе1, (19.18)

Где вектор с имеет компоненты сь С2 и сз [соотношения (19.10)]. Поэтому

£>=Н, (19.19)

Или

Подставив в (19.18) выражение для вектора с [соотношения

(19.10) ], получаем

А = (v0.rxel)xлl. (19.21)

В соответствии с формулой для тройного векторного произ­ведения

Л= —®or tel ■ el) + е (®or *^l) = — ®or + ftj|- ( 19.22) Так как

®«=(®m)„+(пw)i. (19.23)

То из (19 22)

Д= — пi„sinfe, (19.24)

Поэтому

Smg. (19.25)

Аналогичный результат был получен и в статике прямой под­становкой всех величин в г. Проекции динамических сил лобо­вого сопротивления, действующих на движущийся стержень, имеют вид

-Чм (—) sinw(/—(19.26)

I более подробной записи

Япхх~ЯгЛ sin Vg (C0S °—x'i COS uai ДЛ,),

?«л = 9по 5in(f? (—) (—*2Cosc?0l-|-A,,); (19.27)

V vo/

4nt,=g,,o sinҐs (sin a —Л-J cosm^-)- Д^),

Д-г, = Ро [—«jr. (.1 — X

AJT. = Po [tt. r,xiX2 — «jr. (1 — X2)~i~anX2Xs]; (19.28)

Л-'» = Ро [чх, хх'ъ-- ux, x2X3— (1 — Xi ) и, J ;

Cos?,,, = Xi' cos a -)- sin a. (19.29)

При х и х'з, равным сташчес - ким значениям, угол равен ра­нее введенному (в § 11) углу ф,»

Если движение стержня рассмат­ривается относительно состояния равновесия в потоке, то из общих уравнений движения целесообразно исключить статику, тогда в уравне­ния движения войдут только силы, зависящие от движения стержня.

Для этого достаточно из выраже­ний (19.26) или (19.27) вычесть со­ответствующие статические состав­ляющие дпх. , т - е- использовать при решении нелинейных колебаний силы

(</»*,)*='

Определение проекций на неподвижные оси касательной со­ставляющей аэродинамической силы д1# Так как

:Ыёг-<-/1С (—) сов^-йеЩсов^)«?!,

?1л, = Чш (-^Х c°s2 'fe-x’i siSn fcos vu >

01v,= ?lu COE2^-A-'Sign (С05шг),

?1JT. = ?1U cos2Ґy-x'sign(cos %),

Cjdvty

При исследовании нелинейных колебаний следует (аналогич­но силам лобового сопротивления) из выражений (19.32) вычесть соответствующие статические составляющие, что дает выраже­ния для проекций касательной аэродинамической силы на не­подвижные оси

{Яи)&~ Gixt-gix[0. (19.33)

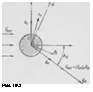
Подъемная аэродинамическая сила qL (рис. 19.2), возникаю­щая только при движении стержня в потоке (в статике эта сила равна нулю). В соответствии с экспериментальными исследова­ниями.[44] модуль подъемной аэродинамической силы определя­ется выражением (рис. 19.2)

У = 4- ‘Mvl - f f-T sin2?*, (19.34)

2 A& v0J

Где аи — угол атаки (угол между нормальной составляющей ско­рости потока ї*пи (см. рис. 19.2) при неподвижном стержне и нор­мальной составляющей относительной скорости потока г7ПОт)- Выраженне для подъемной силы (19.34) справедливо для любых углов атаки а0, так как Сь(аа) определяется экспериментально. При малых углах атаки gi можно ввести

Дс

ClM=-~ Ос, (19.35)

И тогда модуль распределенной подъемной силы

Г I 1 дсг (v„,„)2tll3

С19-36)

ИЛИ

(v X I 1 0cL

(19.37)

Найдем проекции силы на неподвижные оси х«. Вектор, должен удовлетворять следующим условиям:

(?/-«.) =0;

Или в скалярной форме {совместно с соотношением (19.37)]

<?£Л, х + + 4ix, x'd=0;

9iA.(^no, b, + 4trs(^n..Tk+VЈjt, (®«»т)^,=0: (19.39)

?L, I" ?L, + ?L,=?!ooc| ^j4 sin4 Из системы (19.39) находим

?Ј,. = — ha^L sin ^1-j,

Sin^(^), (19.40)

Где

Щ v0

[(О'Л-Яш)лЛ]; (19.41)

—=— [(5.„),л — (®BOt)vs]-

(19.38)

Найдем проекции (г>пот)х,1 входящие в выражения (19.41). Предварительно определим проекции вектора г;пот на связанные оси-

(vnoT-e2) = (®от • ^г) =®от г,^21-Ь®от 1^22 + ^0^8^23; (19.42)

(ийот • ^з) = (®ох*£з) = ®0tjt1&31 + ®отJC2^32 + ®отлгв£33*

Так как

•Уот = от - f" ^Iot =1Ъп от + 1®1ш1 е1 - ( ^9.43)

Из (19.42), (19.43) получаем

®*ог—(®от-^2) ^2+ (®ог**з) <?3. (19.44)

Поэтому

(®лог)*. = (®/.™■il) = (®ot-e2) Л21 + (Пч-Сз) *31.

(7;/гоЛ*а = (^От'^г) *22 Т (7jl0r'^) *32' (19.45)

(®яот)^ = (®от-«2) *23+(®ot-<?s) *33-

После преобразований получаем выражения для проекций подъемной силы:

<7ix, = Qim)cl f—) si п аг [(sin rt — р0и V:) Х2+р0иЛ А-з]: (19.46) VoJ

4u,,=qmfiL sin w](sin« — %a.^x — (cosa — e0c,,) x'2];

Qlx.=4lkcl (^) sin ¥г [(cos a - xi + %u. x,x\.

В статике qLc=0, поэтому (при «<*=0 сь=0)

0?LXl)g=<lLxr (19.47)

Окончательное выражение для вектора распределенной аэ­родинамической силы, действующей на движущийся стержень (до наступления режима обтекания с образованием вихрей Кар- мана)

(Яа)е=Чч— Ча> = (?« — ?«о) + (?1 — ?ш) + ?/.- (19.48)

Силы Кармана. При возникновении вихрей (при числах

Re>40 для стержней круглого сечения) появляются дополни­тельные периодические силы — силы Кармана, равные

1?к1—-гг (о«от)2 s-in ге3т ~ (Яз=ш/Л). (19.49)

2 Лзз

Где я3— безразмерная частота срыва вихрей; ск—аэродинами­ческий коэффициент.

Следует отметить одну физическую особенность сил Карма­на, проявляющуюся при обтекании подвижных стержней. Для неподвижных в потоке стержней круглого сечения безразмерная частота срыва вихрей зависит от числа Струхаля,

. (19.50)

^0

Многочисленные экспериментальные исследования [6; 24; 26; 36; 67] показали, что в режимах докризисного обтекания (при 40<Ке<105) число Струхаля для круглых сечений (среднее значение)

ВЬ^О. г, (19.51)

И частота срывов со линейно зависит от скорости потока.

Для упруго подвешенных стержней (в направлении, перпен­дикулярном потоку) связь между частотой срыва вихрей и ско­ростью потока несколько иная.

На рис. 19.3, а приведен качественный график изменения частоты срыва вихрей для подвижного стержня {49; 64], из ко­торого следует, что при определенных скоростях потока (числах Ре) наступает синхронизация частоты срыва вихрей с собствен­ной частотой колебаний стержня в некотором интервале скоро­стей потока. Если стержень имеет несколько степеней свободы (упругий стержень), то явление синхронизации частоты срыва вихрен и собственной частоты стержня повторяется. В интерва­ле скоростей потока, где имеет место синхронизация, амплитуды поперечных колебаний стержня резко возрастают (рис 19 3, б), где |хзо|—модуль амплитуды колебаний. Наличие диссипатив­ных сил, а также нелинейностей ограничивает рост амплитуд, но они могут быть значительными (например, при галопирова­нии проводов), и при расчетах подобные режимы обтекания с педует предусматривать.

Установить скорость потока voi (рис 19.3, а), соответствую­щую началу синхронизации срыва вихрей с собственной часто­той колебаний стержня можно из условия

Р,=о)=0,2-^-, (19.52)

Где р* — собственная частота колебаний стержня.

С користь потока ощ, при которой синхронизация нарушается, определяется экспериментально [67]. Для стержня круглого се­ления экспериментальные исследования дают следующую при­ближенную формулу для интервала скоростей потока, на кото­ром наблюдается синхронизация [24] (рис. 19.3, а):

(19.53)

На интервалах изменения скорости потока А безразмерная частота п3 в силах Кармана остается постоянной, а амплитудное значение о зависит от скорости потока, что следует иметь в виду при определении амплитуд установившихся колебаний стержней в потоке при скоростях потока, находящихся в ичтер - в ал ах - Уо/ <С

В § 2 говорилось, что для определения подъемной силы, дей­ствующей на движущийся стержень, предлагались различные модели [38; 130].

Ограничимся наиболее простым выражением для силы |дк| (дополнительной к силе 1 gL|). когда аэродинамический коэффи­циент си считается постоянной величиной в определенных ин­тервалах чисел Не. Статистические исследования показызают, что среднеквадратичные значения коэффициента ск в интервале 0,5-106<Ке<2-106 изменяются незначительно [24]. Это можно считать обоснованием принятого допущения о постоянстве ко­эффициента ск. Вектор дк, как и вектор дс, ортогонален мест­ной нормальной составляющей относительной скорости ьп0т. Распределенные силы Кармана должны удовлетворять тем же соотношениям, что И СИЛЫ дь, т. е.

(19.54)

(19.55)

Для определения проекций силы дк на неподвижные оси по­лучаем систему уравнений

(19.56)

(19.57)

(19.58)

(19.59)

Опуская промежуточные выкладки, получаем

8іпю^5іп«3г: (19.60)

?,<*,= Sin % Sin mxi (19.61'

?“-=fa (V-) (-^) sin sin (19-62>

Где

—=[(sin a — X2+ft,« с»Хз];

"c

—=[(sina — yt^x'i — (cosa - р0ы^,)JC3]; (19.63)

— = [(cos a — PbBx.) -*2+] • v0

В статике <7Ko=0. Полная аэродинамическая сила, действую­щая на движущийся стержень при отрывном обтекании,

*?о=(4?« (#i ~ <7io) (19.64)

§ 20. Аэродинамические силы, действующие на стержень при малых колебаниях

При исследовании малых колебаний стержня в потоке с уче­том возникающих при колебаниях дополнительных (по отноше­нию к аэродинамическим силам в статике) аэродинамических снл, необходимо получить выражения для аэродинамических сил, линейно зависящих от скоростей и смещений точек осевой линии стержня.

Для малых аэродинамических сил введем следующие обоз­начения:

&4nxr Mxi И ДqLXi.

Относительная скорость vOT при малых йх

®ot=®c [ * “ % (cos a - uXl + sin a • ux^ ^p0 = . (20.1)

Считая uXi и ux. малыми и разложив выражения для дПх1, Я.х1 и Qlx. в ряды, после преобразований получим линейную часть малых аэродинамических сил.

Проекции аэродинамической силы лобового сопротивления Ад„ {kqnx;)- При малых колебаниях стержня из соотношений

(19.26) можно получить следующие выражения:

Мпх1=(ай )и‘х1 - J - а1 )их% - J - а& (aS*uXt + a$*iix% - f-

+a%}ux3) - J - qn0pa sin <рс [clXux - J - cl2ux, --ci2iiX3), (20.2)

В векторной форме записи

Дqn=А{ 1 hi' - f - Л(2)к - f - sin yaCbu. (20.3)

Элементы матриц Л*'), А& и С0 даны в приложении № 1.

Проекции каса! ельной аэродинамической силы &qi(&q1X[). Из соотношений (19.32) после преобразований получаем дqlx,=(a(t? uXl - f - а{пи'х% +я! з)«**) + (a^?uXl - f - а$иХа-f-а?Их3), (20.4) в векторной форме записи

Д q1=A^u,-- А<*>и. (20.5)

Элементы матриц А^3) и Л<4> даны в приложении № 2.

Проекции подъемной касательной аэродинамической силы

При малых колебаниях полагаем

?tooCt=?Јoo4^-“0=?io“0- (20.6)

Oaa

Угол атаки ас считается малым. Так как aa является общим множителем в выражениях для Qlx^ остальные сомножители в выражении (19.46) можно взять равными их значениям в стати­ке, ЧТО приводит к следующим выражениям ДЛЯ Ауьх] •

AqLxx=qu№a sin Va sil1 “*^20.

AqiXa=qL(fia sin tpfl(sin — cosa-^S0) * (20.7)

AgLxa = qL(P>a sin Cos a --«20-

Найдем зависимость угла aa от цх. и их.. Рассмотрим рис 20.1. Угол атаки иа есть угол между проекциями векторов vno и vn0i на плоскость (ёг, ёз)- Так как угол сса считается ма­лым, можно положить (при малом и)

Vn0—lu2l

ГДе VnQ= Vo Sin (fal -

Представим вектор и в виде суммы векторов u и иПу как это показано на рис. 20.1. Вектор и лежит в плоскости векторов с н i»o - Вектор ип перпендикулярен этой плоскости. Проекция век­тора и на направление Ъ равна

Их=и,-е (20.9)

И равна проекции вектора tin на ёь так как

(я„-е1)=0, (u-e1)=(uil-^i). (20.10)

113

Аналогично может быть получено равенство

(и •t'o) — (ии *®о). (20.11)

Обозначив угол между ii\ и 7 через у, получаем следующие соотношения:

Eos — Y)=cos <рЙ1 cos Y + sin <?Cl sin Y; (20.12)

Cosv = -fe^-=-пЈ3-; (20.13)

J«ll| иц

~Ш^~= ^ f- +^J^V«U 1-(иГеу. (20.14)

|ztu| t/0 ®b |«n| |«ii)

Из равенства (20.14) определяем

G|iP_(« ^o)2 —2 (t/p-gj) (и -^o) ju - ei) + (к-ei)24 ^20 15)

Из равенства |ы|2=|иц|2+1и»|2 определяем q |2= 4 sin2 ?а, ьf — (ы-щ)2 + 2 fo. gj (ц. р0) (ы-йj) — (ь-liY v% s, n2 Va

(20.16)

Окончательно по формуле (20.8) получаем выражение для угла атаки

Sm2уа |и|2 — (к-г^о)2 — vo^u'e^ +2(v*ei) («*^o) («*ei) a„= 1 « .

Ь0 Sllо" fa

(20.17)

Рассматривая угол атаки как функцию трех переменных й3, разложим функцию (20.17) в ряд Тейлора в окрестности точки

(0; 0; 0), ограничиваясь линейным приближением (щ—малы),

O. a=F(u Cl, iixi, иКз)=—^—uVl ^ - Нля -}—V"- - и va. (20.18)

DUjj.

После преобразований из (20.18) полагаем выражение для угла атаки:

Ой=-------- ----- х2п sin а ■ их~^ (-^ю sin «—х30 cos а) аХл - J-

Vq Sltl2 <f>a

+ A:20cosaBj. (20.19)

Определив a„, получаем

Д to,=(ag’u,, + ад’йл j-ofiij; (20.20)

В векторной форме записи

AgL=A^u. (20.21)

Элементы матрицы Л(5) даны в приложении № 3.

Определив (Ajn), (Atfi), (Д<?ь), находим полную аэродина­мическую силу при малых колебаниях стержня в потоке:

Д^в=(А<1> + Л<*)) «Ч“И(2)+?лоРо sin <рЙ1С0+Л<4>-М<5>) и. (20.22) Аэродинамические силы с учетом продольного движения стержня. В этом случае относительная скорость движения точки (сечения мыслимой безынерционной трубки, в которой движется стержень) на расстоянии е от начала отсчета равна

— —w. (20.23)

Полная аэродинамическая сила qa, действующая в сечении с координатой е (как и при гу=0),

(20.24)

Где qn и qx зависят от квадратов проекций vm на нормаль к осевой линии стержня и на направление касательной. Модули сил (]„, Ql и Ц (в безразмерной форме) вычисляем по формулам

Fow)2^-=g„0 ; (20.25)

L? J = Y CiPd (®»or)2= Qmf,. ( -^-j ’ (20-26)

То выражения для проекций qnXt и qLxj совпадают с выраже­ниями (19.27) — (19 46).

Рассмотрим выражения для |<yi|. Проекция относительной скорости на направление касательной к осевой лицни стержня

(Л) 1=&гг ei) = (vQ ■ ei) -(a-е i)-~(w-el)=‘vKI cos a-x--

-{-Vq sin ах'з—uXlx{ — uXjtX2—uXax&—w. (20.29) Поэтому переходя к безразмерной форме записи йХ{ и w, по­лучим

(®ot)i —% [Cos aX'l 4" sin а - х'з — P(IW — p0 (aXlXl - f - иХлХ2 + йХгх'з)].

(20.30)

Подставив (20.30) в (20.27), после преобразований имеем Ы = <?ю [cos2 <pat + pa®2 + рОD — 2 cos o'® — 2 COS <ра, ppDj -}-

+ 2&WDJ, (20.31)

Где

A=uXlx[ 4- uXax2 4- Ux. xs-t

(20.32)

Cos <pCl = cos a • x[ sin а-лгз.

Проекция вектора qt на неподвижные оси

Ях=дix't sign (*ЈJi(/= 1. 2, 3). (20.33)

Проекции силы qi при малых колебаниях Aqlx. f Из соотно­

Шений (20.33) получаем

Aqixl=(a(nUXl 4- a{$uXi 4- а!1}«^3) 4~ (®fi9)ir. 4“ a$>«.v, 4" «и}«*,),

В векторной форме записи

Afc=А<8>й' 4- Ai9iu. (20.34)

Элементы матриц Л<8> и А& даны в приложении № 4.

Силы Кармана при малых колебаниях стержня. Аналогично тому, как это было сделано при определении AqnJcr из (19.60) — (19.62) получаем выражения для АдКХ{

АдК{=(aiPu'Xl4-а$иХл 4-аf }»*3) sin пъх(a(,PiiXl с$их% 4~

]-aS ‘ux^ sin /г3т, (20.35)

В векторной форме записи

Ддк—А<6)и* sin щх-- Ai7)u sin пАX, (20.36)

Где элементы матриц Л<6* н Л(7) даны в приложении № 5.

Полная сила Кармана

?к=?«о + й? к. (20.37)

Где <у„о — сила Кармана, действующая на неподвижный стер­жень; Адк — дополнительные силы, вызванные движением стерж­ня (с учетом малых их и иХ[)

Для криволинейных стержней местная нормальная составля­ющая относительной скорости потока, от которой зависит мест­ная сила Кармана, определяется координатой к, поэтому синх­ронизация частоты срыва вихрей с одной из собственных частот тоже имеет местный характер, т. е. иа одинх участках стержня (например, провисающего провода линии электропередач) час­тота срыва вихрей равна собственной частоте колебаний стерж­ня, а на других продолжает расти с ростом местной нормальной составляющей скорости потока, что существенно осложняет чис­ленное решение уравнений движения.

§ 21. Уравнения движения стержней, взаимодействующих с внешним потоком жидкости или воздуха

Векторные уравнения движения стержня. При движении эле­мент стержня имеет поступательную скорость V и угловую ско­рость со (рис. 21.1). На элемент стержня в общем случае могут действовать распределенные силы д и момента р., не связанные с потоком, а также аэродинамические силы и моменты, возни­кающие при взаимодействии стержня с внешним потоком да и рс. На элемент стержня, пока­занного на рис. 21.1, действует сила инерции

DJ = — й т——^ (с1т

И (если учитывать вращения элемента) инерции, равный

Где У — диагональная матрица, элементами которой являются главные физические моменты инерции элемента стержня, дчппа которого равна единице Входящая в соотношение (21.1) масса единицы длины т0 и элементы матрицы / могут быть и пере­менными по 5 (для стержней переменного сечеиия). Для нерастя­жимого стержня дуговая координата элемента стержня 5 оста­ется неизменной при движении, поэтому при описании движения можно использовать переменные Лагранжа, что позволит перей­ти в (21.1) и (21.2) к частным производным по I, т. е.

СП„=-йт — ам„=------------------ —

Д( дг

Рассмотрим стержень, у которого центр тяжести сечения совпадает с центром жесткости (рис. 21.1).

Воспользовавшись принципом Даламбера, получаем вектор­ное уравнение поступательного движения элемента стержня:

Если учитывать инерцию вращения, то уравнение вращения элемента стержня относительно центра тяжести имеет вид

—— (Уш) = ———~е х (21.4)

Приведем уравнения (21.3) и (21.4) к безразмерной форме записи, полагая:

*=А/> (О)//3, |Л=;х°Л33 (О)/13; а)=иРр0; и=у—1?Чр0;

А1=Л1Ы3,(0)Ц; £=УМ,3(0)//2; 5=£/,

Где т и 8—безразмерные независимые переменные; р0= =[Л3з(0)/то(0)/4],«> где /7г (0) —масса единицы длины стержня в начале координат, Лгз(0)—изгибная жесткость в начале коор­динат. Для сгержня переменного сечения

Т (е)=ти (0) По (е), (21.5)

Где п0(е)—безразмерная функция; т0(0) =р/70; Р0 — площадь поперечного сечения стержня в начале координат; р — плотность единицы объема стержня. Матрицу / можно представить в виде

(21.6)

Где

[/«— моменты инерции сечения относительно главных осей се­чения («=2 и I—3) и относительно осевой линии стержня

(/=!)]. При переходе к безразмерной форме записи уравнения движения принимают следующий вид (опуская индекс нуль в безразмерных величинах):

(21.8)

-£-(у<г»)=-^-+г1хс+|1+|:<1, (21.9)

Где ;°=№/2.

Переходя к связанным осям (к локальным производным) по­лучаем следующие уравнения:

Л°("!г}_| ‘“х®=-§-+*х«+?+?а; (21.10)

Л +“ х ; х ж+ё, х <у+н - (2i. li)

Дополнительно к уравнениям (21.10) и (21.11) имеем еще векторные уравнения (в безразмерной форме)

УЙ = Л (* —Кр) + Л (^о — *оо); (21.12)

-~ + *Х;в-('»хё1)=0; (21.13)

+ (21.14)

Ш= (21.15)

Где А — диагональная матрица безразмерных жесткостей. Мат­рицы Ь и Ь (см. § 3) характеризуют вращение базиса {?*} от­

Носительно базиса {ёго}- Система шести уравнений (21-М) — (21.15) содержит шесть неизвестных векторов: V, (>, М, к, со, {К Остановимся подробнее на втором слагаемом, входящем в урав­нение (21.12), которое представляет собой вектор М0, компонен­тами которого являются компоненты момента в статике в бази - се {Ёа}. т. е.

Л/0 = Л(х0-^0), (21.16)

Где иоо — вектор, характеризующий геометрию осевой линии стержня в естественном состоянии для «жесткого» стержня или в заданном поле сил (для гибкого или абсолютно_гибкого стерж­ня) до нагружения аэродинамическими силами; к0 — вектор, ха-

119

Растеризующий геометрию осевой линии стержня в новом со­стоянии равновесия. Векторы хо и кш соответственно равны:

Где компоненты хоог и хоі есть компоненты соответствующих век­торов в исходных базисах {ёгоо} и {ёг-0}, т. е.

Вектор

7й0 = V M0tлi7 (21.18)

Где Moi — компоненты вектора в статике {в базисе {с, о}], поэто­

Му уравнения (21.12) можно представить в виде

7Й=Л(х-х0)+ЛТ0. (21.19)

При решении конкретных задач часто являются полезными следующие дополнительные векторные уравнения:

-£-+* XЙ=(1 (21-20)

— щ——шхї=0, (21.21)

Де. От

Где й — вектор перемещений точек осевой линии стержня отно­сительно состояния равновесия. Векторы v и й связаны урав­нением

Г_ Дй

Du

V=—+i0XU. (21.22)

Система уравнений (21.10) — (21.15) получена в связанной системе координат. Возможны и смешанные варианты уравне­ний, когда часть уравнений записывается в неподвижной системе ксординат, а часть в связанной. Например, если надо знать аб­солютные перемещения точек осевой линии (проекции вектора перемещений в неподвижных осях), то целесообразно уравнения

(21.8) , (21.13) и (21.22) использовать, не переходя к локаль­ным производным, т. е. в виде

Л «0_+-+- (2123)

Ох де

Уравнение (21.20) до перехода к локальным производным имело вид

(21.25)

Де

Поэтому, переходя в правой части к базису {і,}, получим

*1—^10=(21.26) / і

Где кі, — элементы матрицы К преобразования базисов {і.} и {ёг}; к0 — элементы той же матрицы в статике, поэтому уравне­ние (21.24) принимает вид

(21.27)

Следует помнить, что в уравнениях (21.23), (21.24) и

(21.27) векторы представлены через компоненты в базисе {^}, т. е.

“=2“-*^,; *=2«*а- ]~і 1 /-1 /-•

Но тогда следует перейти к компонентам в базисе {/э} и в векторе <), входящем в уравнение (21.11), так как все векторы, входящие в уравнение (21.11), записаны через проекции в бази­се {ё*},

(21.28)

/=і /=і

Используя соотношение

}] = ^кіГеп (21.29)

0(=2<ЬА/- С21-30)

/=1

Зто выражение можно представить в виде векторного равенства

(21.31)

Где @е—вектор, имеющий компоненты <2,; @х — вектор с компо­нентами QXj, /С — матрица преобразования базиса {г,} к базису

{?і}. Элементы матрицы Д (/г^) зависят от трех углов: 0, ф и характеризующих взаимное положение векторов базисов {Г,} и {ё,} Для вектора у. можно получить выражение через элементы матрицы К, используя соотношение

(21.32)

И переходя в этих соотношениях к базису {7,}. После преобра­зований

У1=^3]

«а=*п ^ > (21-33)

(21.34)

Где О V — вектор, компонентами которого являются углы, харак­теризующие взаимное положение единичных векторов базисов И И {?:}■

Для получения уравнений в более компактной форме записи (где это удобно) в дальнейшем для углов приняты следующие обозначения: для углов, характеризующих взаимное положение базисов {ё»} и {ёго}, принято ^>=■0'!, ^=-Ог, <р=‘0,з; Для углов, ха­рактеризующих взаимное положение базисов {ё,} и {Г,}, приня­то &=©>„ ф=в^гг, 9=®,дГз. Окончательно получаем следующую систему уравнений, в которых введены обозначения: векторы с индексом х-—это векторы, компонентами которых являются проекции в неподвижных осях, а векторы с индексом е — это векторы, компонентами которых являются проекции в связанных осях, т. е. имеем

<21-35)

■1° х '«>' — — *„ X М,—е1 X =ре; (21.36)

М=А(*е-е)+7Й0е; (21.37)

■*.е=к^

Ш е=К™

Яе-=КС}Х.

В результате имеем семь уравнений с семью неизвестными векторами: ї<х, ()х, (Л>, М0, (ое, - кР, #д.

Уравнения движения в скалярной форме записи. Получим уравнения движения для двух вариантов записи систем (21.10) —

(21 15) и (21.35) — (21.41) в тензорной форме записи и в более

Подробной форме записи. Система уравнении (21.10) — (21.15) в тензорной форме записи принимает следующий вид:

(21-42>

Л, ^ + Е.^Л=у+=;|Л-«;+^'й+1+Р..; (21.43)

Л1„=ЛЯ|»Г-^Т)+АГ0«; (21.44)

0; (21.45)

Ч = (21.46)

Ш(21.47)

Дг

В более подробной форме записи имеем

^г’3“21,2,03)—йТ"—^3*2 ®2%3 ~41 ~ ч“'=

Пс(-^- + »1“з-®л)--^— 0л + Сл-<?2-?«,=°. (21.48)

Ли ®2Ш1 — ‘»л) — 02к1 + Сі*2 —Ч% — Ча, = 0;

А ■^ + (А,-А)«ч»!!-^М3+хз, И2-^-|хо1 = 0;

ОС ОЕ

А-^ + (А - А) ->,"'3 - —1 - - + *.-И3

Дт> де

(21.49)

^33 р Ь (*^22 — «/а) <|>1(й2 Х1Ж2 у-2^I — ^2 !А3 — !АЙ3 = 0;

Л1,*^+Мт;

М2=Ая(ъ -*») +Л*® (21-50)

ЛГ*=-Азз(**—**>) НЛ'оз;

-“■ + ®3*2 - ®2*3=0;

-^р, — 'УзУ-л = <.03; (21.51)

Дия |

— Г^1 — »1*2= — ш2;

*2=^(4;> -^-+^); (21.52)

У“1

— V1 /{1} А&1 • Ш — V1 А1) ^2 . —VI А1) ^3 Г91 поч

0)1 2/1' “5г ’ 2_ Лг' * 3"2^3/ “^г * ( 3)

У=1 7=1 /-1

Система уравнений (21.35) — (21.41) в тензорной форме при­

Нимает (после исключения из уравнения (21.36) вектора <?е) следующий вид:

Дьх д(^

«0-^=-^ +?*„ + ?«„; (21-54)

Л г" ^ 4’ (ек(/й^лшт^==“^"_1_Ек'7у'^/“Ьек(»^1Р^лгр-Ь! Ак"Ь^вк;

(21.55)

-*^к==-^кТ (К1 *от)4"-^0к> (21.56)

-^- = (ки-к%)1к,, (21.57)

ДЪх

(21.58)

В подробной форме записи система (21.54) — (21.58) имеет вид

«о-гг----------------------- + (21.59)

«о-

А—+(Л - А) »,«>8 -—- чЩ+*^3+

Дх ' де

+ 2*Лр=Ь+М (21.60)

/-1

У3°3 +(л°2 - Л) «*»» -

Дтз д&

—2 ^2рО*р ~ "Ь ад

Р-1

Ж1=л.('-1-*ю)+М01;

Ж2=Л22СХ2 — х2о)4~^02> (21.61)

-М3=А зз (*3 *з0) -}- М03;

-^- = (*„-*1,), =(*12—£12); -^-=(А13-А? з); (21.62)

*» = 11Л5])-^-; (21-63)

(21.64)

Уравнения движения стержня в плоскости потока. На

Рис. 21.2' показан гибкий стержень, форма равновесия которого

В покоящейся среде есть плоская кривая. Если стержень имеет се­чение, одна из главных осей ко­торого перпендикулярна к плос­кости, в которой располагается осевая линия стержня, то при действии потока, параллельного этой плоскости, перемещения стержня будут происходить

В плоскости потока. В рас­сматриваемом случае имеем к3=‘У3=“і=«2=0; $=«Ь=0; ^=*2=0; Оа==М1 = М2=0; д3= =<7а3=0; |і,=іЛд.=0. Из уравнений (21.59)—(21.64) долучаєм (смешанный вариант уравнений)

9с Г,(~) sin ^1^2 — Ро*2 Pox'ix'wjcJ - j - J cos2 ygx’i;

(21.70)

Яах* = ЯпЬ Sin 9g[-XiX2-~%{x[xiiXl—x[ Ux,)-f-

“b <7io ^ cos2 <Pg'X2> (21.71)

Где <vOT=v0 [(1 — %uXlf - f $iil,-f-J; cos 'fg=

= lf^X ^ ~ &“*») x'l — %йл:ax'2]; sin cp^=^l —COS2cp^.