КОТЕЛЬНЫЕ УСТАНОВКИ И ПАРОГЕНЕРАТОРЫ

Течение однофазного потока в трубах

Движение однофазного потока (жидкость или пар при докритиче - еком давлении, теплоноситель при сверхкритическом давлении) описыва­ется уравнениями неразрывности (8.2), (8.3), движения (8.11), (8.12), (8.14), энергии (8.16), (8.18), (8.20), состояния, а также заданными начальными и граничными условиями.

Для использования уравнений состояния, показывающих зависи­мость р, у, ср, р и других параметров воды от температуры и давления потока, необходимо знать структуру потока, распределение температуры, Давления и скорости потока по длине и сечению трубы. При проведении тепловых и гидравлических расчетов принимается, что давление в потоке но сечению постоянно, т. е. изменяется только по длине трубы.

Структура однофазного потока жидкости характеризуется непрерыв­ным гладким изменением плотности ее по сечению и длине трубы, а также

9 Котельные установки

Во времени. При этом поля температуры и скорости потока тоже непрерыв­ны и гладки в пространстве и времени (рис. 8.3). В любой момент времени отдельная частица движущейся жидкости имеет определенную по величине и направлению скорость.

В одномерном приближении описания движения жидкости в трубе (по оси трубы) принимается, что температура и скорость потока постоянны по радиусу трубы (в ее сечении) и переменны по ее длине. Следовательно, температура и скорость потока усредняются по сечению трубы. При этом характеристика жидкости и потока также принимаются постоянными по сечению потока.

Характеристики течения однофазного потока в стационарных

Условиях

Из уравнений неразрывности (8.5) по известному расходу массы жид­кости G можно определить массовую скорость потока pw, кг/(м2-сек):

Pw = G/f.

Эта величина постоянна по длине трубы (при ее постоянном сече­нии /). Зная в каком-либо сечении трубы плотность жидкости рж, можно определить среднюю скорость ииж в этом сечении:

Ыж = {pw)/p7K. (8.26)

Для определения плотности жидкости рж по уравнению состояния р = = р(р, t) или р = р(р, h) необходимо рассчитать среднюю энтальпию по­тока кж в данном сечении по известной величине энтальпии /гвх на входе в трубу или ее участок. При этом используется уравнение (8.21):

Pw - f

Давление рж в рассматриваемом сечении определяется по давлению на входе в трубу рвх и перепаду давления на участке Ар (8.14):

Рж = Рвх - Ар.

Полученные значения рж, Нж используются для определения в данном сечении V, Ср, /І, Л и т. д.

При расчете перепада давления Ар на участке длиной I необходимо знать среднеинтегральные значения плотности рс? и удельного объема жидкости:

І і Рср = ] J pdl; vcp = ± J vdl (8.28)

О о

Практически, средние значения плотности и объема воды и пара при докритическом давлении и водного теплоносителя вне зоны большой теп­лоемкости при сверхкритическом давлении можно определять по средней энтальпии потока hcp:

Hcp = [К - М/2,

ГДе /гн, hK — энтальпия потока в начале и конце участка, кДж/кг.

Средние значения плотности и объема в зоне большой теплоемкости = 1600 - г 2600 кДж/кг) определяется по формулам:

= h _ ь------------ ; (8.29,а)

Г1 к flH

= h --—' (8.29,6)

ГДс Рк. Рн, ''к, ї'н определяются по hK и /?,„. 9*

Течение двухфазного потока в трубах

Для описания течения двухфазного потока (пароводяной смеси) ис­пользуются две модели. В модели гомогенного потока принимается, что обе фазы (жидкая и паровая) распределены равномерно и непрерывно одна в другой, при этом скорости их движения и температура одинаковы. Другими словами, в гомогенном представлении движения двухфазного потока рас­сматривается как течение однородной сплошной среды. Полученные при этом параметры и характеристики потока называются расходными. Вто­рая модель рассматривает двухфазный (гетерогенный) поток как систему из двух фаз, разделенных межфазными границами, движущихся с разны­ми скоростями. Уравнения записываются отдельно для жидкой и паровой фазы. Начальные и граничные условия также записываются для фаз, при этом учитывается, что на границах раздела фаз имеют место механическое воздействие, массообмен и переток теплоты. Параметры, характеризующие движение каждой из фаз в отдельности или поток в целом (с учетом дви­жения отдельных фаз), называют истинными параметрами.

В инженерных расчетах за основу расчета двухфазных потоков берется модель гомогенного потока, по которой определяются расходные парамет­ры, а по ним рассчитываются истинные параметры с привлечением экспе­риментальных данных, устанавливающих зависимости между расходными и истинными параметрами двухфазного потока. Соотношения между рас­ходными и истинными параметрами двухфазного потока имеют сложный характер и зависят от структуры потока и распределения скоростей фаз. Структура двухфазного потока показывает объемное содержание паровой и жидкой фазы, их границы, распределение по сечению трубы. По мере нагрева (охлаждения) потока массовые и объемные доли фаз изменяются, что сказывается на структуре потока и скоростях фаз. Предельными случа­ями являются однофазные потоки жидкости (масса пара равна нулю) и пара (жидкость отсутствует). Между этими крайними случаями можно выделить ряд устойчивых сочетаний структуры потока и скорости фаз, характеризу­емых режимами течения двухфазных потоков. Каждому режиму течения можно соотнести свои зависимости между расходными и истинными пара­метрами двухфазного потока.

Расходные параметры двухфазного потока. Возь­мем участок обогреваемой трубы длиной I (рис. 8.4). Плотность теплового потока qi, кВт/м, постоянна по длине трубы. На вход в трубу подаем воду о расходом Go, кг/с, и энтальпией ho, кДж/кг. На экономайзерном участке Uк происходит нагрев воды до температуры кипения ts (энтальпия воды на ли­нии насыщения h'). Давление потока р на рассматриваемом участке считаем постоянным (перепад давления мал). В гомогенном потоке фазы находятся в термодинамическом равновесии. При энтальпии потока h > /?/ начнется

| | | | | | |

- . -

Образование паровой фазы. Массовый расход паровой фазы обозначим D, кг/с, а расход жидкой фазы (воды) GB, кг/с. В сечении Z суммарный расход паровой и жидкой фаз G равен

G = D + GB.

По уравнению неразрывности (условие сплошности) G = Go = const.

Суммарно количество теплоты, переносимое двухфазным потоком через сечение Z:

GhCM = GBh! + Dh" = GBh! + D{h' + r), (8.30)

Где h" — энтальпия пара на линии насыщения, кДж/кг, г — скрытая теплота парообразования, кДж/кг; hCM — энтальпия пароводяной смеси. Отсюда

HCM = Q^-h' + ^r = ti + x-r. (8.31)

Величина х представляет собой расходное массовое паросодержание и характеризует долю пара в массовом расходе смеси:

Х = D/G. - (8.32)

Тогда расходное массовое содержание жидкости будет равно

1 - X = GB/G. (8.33)

Для равновесного двухфазного потока

Величину х еще называют относительной энтальпией потока. Для жид­кости, недогретой до tS9 получается х < 0; для жидкости на линии насыще­ния х = 0; для пара на линии насыщения х = 1; для перегретого пара х > 1. По уравнению энергии (8.21) в сечении Z

HCM = h> + qi{Z~l™ (8.35)

При этом величина х будет равна

Х = (8.36)

Длину экономайзерного участка 1Ж можно определить, записав для него уравнение энергии (в виде теплового баланса):

= + (8.37)

Отсюда

1ж = Go(h' - ho)/qi = G0 • ДЛ„ед/я, (8.38)

Где Д/і„ед — недогрев воды на входе в трубу до значения энтальпии воды на линии h! кипения.

Подставляем /эк в выражение для х (8.36):

Х ~ ~ —у^ — • Z — Ажнед '(8.39)

Или

Ql_ rG

Полученные формулы дают возможность в любом сечении трубы опре­делить массовое паро содержание х, массовый расход пара (xGo) и воды ((1-х)-Go).

По массовым расходам пара и воды можно определить расходные ско­ростные характеристики двухфазного потока:

— приведенные скорости жидкой и паровой фаз — скорости, которые име­ли бы жидкость и пар, если бы только жидкость или только пар зани­мали все сечение f трубы:

°° tv7' ,840)

Где р р" — плотность воды и пара на линии насыщения, кг/м3;

X - f~ Д^нед — 7-7 '

- скорость циркуляции — скорость, которую имел бы поток, если бы его плотность была равна плотности воды на линии насыщения:

^о = 75 (8.41)

- скорость воды на входе в трубу:

Wbx = 7^-, (8.42)

/ ' Рвх

Где рвх — плотность воды на входе в трубу;

- скорость пароводяной смеси

WCM = 7-^-, (8.43)

J • Рем

Где рш — плотность пароводяной смеси.

С учетом введенных понятий о скоростях уравнение неразрывности можно записать в виде

G Go, w'0 , „

J = y = wbxPBX = тр = iZ~x, p ~ = WcmP™ = PW) = const-

(8.44)

Из этого равенства можно определять искомую скорость через любую из­вестную.

По длине трубы приведенные скорости воды и пара изменяются. Какое между ними соотношение? В сечении Z массовый расход смеси G = D+GB представим через скорости wq, wf0 и Wq :

Wop/f = w^pf/f + w,0p/f.

Отсюда

Wo = w'0 + • p"/p'. (8.45)

Получается, что хотя и Wq изменяются по длине канала (шд умень­шается, a w'q растет), но сумма wf0 и w'q р"/р'постоянна и равна скорости Циркуляции.

По массовым расходам жидкости GB и пара D можно объемные рас­считать расходы жидкости VB и пара VTU м3/с:

В гомогенном потоке скорости фаз равны, поэтому объемный расход пароводяной смеси VCM, м3/с, будет равен сумме объемных расходов воды и пара:

Км = VB + V„ = G/pCM. (8.47)

Объемные расходы выразим через скорости wCM, w'Q и w'q

WCm • / = Ч/ + W0 f

Или

Wcm =w'Q+w'o. (8.48)

Сделаем преобразования:

= (1 - х)Ц + хЦ-г - - L = (1 - + xr (8.49,а)

Рем р! р" PzM р! р"

Принимая, что удельный объем v является обратной величиной р, получим

Уш = (1 - x)vf + xv" = vf + гф" - vf). ' (8.49,6)

Для характеристики объемных расходов воды и пара вводится расход­ное объемное паро содержание /3 и водо содержание 1 — (3:

P = V - = vTv' (8-50)

УВ ^г Уи ^см

Значение /3 может быть выражено и через скоростные характеристики:

= (8-50)

Шсм год + Установим связь между (3 и х:

0 = 1 + Vs/Vn = 1-х р» = х + (8,50)

Х р'

Зависимость /3 от х для некоторых значений давления потока показана на рис. 8.5. При критическом давлении р" — pf, следовательно, /3-х.

Расходная плотность пароводяной смеси определяется из выраже­

Ния

Л = G_ = Ов + £> (8 53)

' см у v - I - V ' ^.jj/

'см г v,]

Проведем преобразования этого выражения:

GB + D VBp' + Vnp" (1 - 0)VCMp'+ pVCMp"

Рем =

P> - (3{p> - p"). (8.54)

Истинные параметры двухфазного потока. При дви­жении пароводяной смеси действительные скорости паровой и жидкой фаз различны. Истинные параметры двух­фазного потока могут быть определе­ны, если известна структура потока. Важной характеристикой структуры потока является распределение паро­вой и жидкой фаз по сечению тру­бы. Через определенное сечение трубы в разные моменты времени проходит различное количество паровой и жид­кой фаз, т. к. структура двухфазного по­тока не однородна, но усредненные по времени значения части сечения тру­бы /, по которым проходят паровая /п и жидкая /в фазы, являются для дан­ных условий статистически устойчи­выми величинами. Доля сечения, заня­тая паром, называется истинным объ­емным паросодержанием ср:

Fn

/п + /в

С помощью величины ср можно определить действительные значения ско­рости паровой w* и жидкой м/с, фаз:

А, <Pnf

Ff'fn

Шп

P'U-U) 'W

Возьмем отрезок Az трубы, по которой движется двухфазный поток. Суммарная масса обеих фаз в объеме / • AZ будет равна

P'(f-fn)-AZ + p"fu. AZ.

Если эту массу разделить на объем / • AZ, то получим среднюю плотность, которая называется истинной средней плотностью двухфазного потока рШ) кг/м .

P'(f-fn).AZ + p"fnAZ, Рем = f~AZ = Р ^ = 9 ~р (8,58)

Из этой формулы выразим величину истинного паро содержания

¥>=^7- (8-59)

Р - Р

Видно, что <р характеризует среднюю плотность двухфазного потока и из­меняется от 0 (при рсм = р') до 1 (при рсм = р"). Плотность рсм можно определить экспериментально (например, просвечивание потока 7-лучами), следовательно, появляется возможность определения величины (р.

Действительную скорость пароводяной смеси wCM определим из соот­ношения

WmPcM = WQ - pf.

Отсюда

Wo - р ™о'Р WQ /о

Wcm = —д--- = —------- т,------ J7Z = --------------- 7Z ТГГТ' (8-6°)

Рсм рг _ _ р//) і - (^(1 - р'Чр')

Таким образом, истинные значения скорости фаз, средней плотности и скорости пароводяной смеси могут быть рассчитаны, если известна вели­чина истинного паро содержания (р.

Соотношения между расходными и истинными параметрами двухфазного потока. Как уже отмечалось, рас­ходные параметры рассчитываются по уравнениям для гомогенного потока, когда скорости жидкой и паровой фаз принимаются равными. В действи­тельности, скорости фаз различаются. При подъемном движении в верти­кальной трубе истинная скорость паровой фазы больше, чем скорость жидкой фазы а при опускном движении — наоборот. Разность скоростей фаз называется относительной скоростью фаз:

Wan (8.61)

При подъемном движении Worn > 0, при опускном движении W0Tн < 0.

Коэффициент (фактор) скольжения фаз показывает отношение истин­ных скоростей фаз:

5 = w*/u%. (8.62)

Для подъемного движения s > 1, для опускного движения s < 1. Для гомогенного потока по определению 5 = 1. Для реального двухфазного потока коэффициент скольжения является функцией многих параметров и определяется экспериментально.

Проведем преобразование выражения (8.62), используя выраже­ния (8.40) и (8.32):

О =< = < 1~(Р = 1~(Р х vR

Wl Ч> wf0 Ч> 'p»'l-x' 1 ;

Отсюда получаем зависимость между ср и х:

Р Х

При критическом давлении р' = pf W* = w* и коэффициент скольже­ния s = 1. В этом случае ср = х, т. е. истинное и массовое паросодержание равны. При докритическом давлении р"/р' < 1 и ср > х. Соотношение между ср и р через S

У =------------- = т;—Л------- = С • р, (8.65)

Где

C = l/(P + S(l-0)). (8.66)

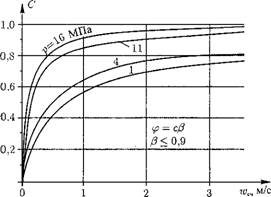
При равенстве скоростей фаз S = 1 и ср = р. Для реального двухфаз­ного потока: при подъемном движении 5 > 1, величина (/3 + 5(1 - Р)) > 1, С < 1 и ср < Р; при опускном движении S < 1, С > 1 и ср > р. На рис. 8.6 показана зависимость коэффициента С от скорости смеси wCM для нескольких значений давления при подъемном движении среды в верти­кальной трубе. Эти данные справедливы для р < 0,9. Коэффициент С можно выразить через скорости w* и w%M:

Где ^cxf' — скорость подводящей смеси при равенстве скоростей фаз (для гомогенной модели); С = w^' /w^.

Коэффициент С показывает соотношение скорости пароводяной смеси, полученной для гомогенного потока, к действительной скорости пара.